DGL教程--DGL概览
Note:
Click here to download the full example code
DGL at a Glance
Author: Minjie Wang, Quan Gan, Jake Zhao, Zheng Zhang
DGL是一个Python软件包,致力于在图上进行深度学习,并在现有的张量DL框架(例如Pytorch,MXNet)之上构建,并简化了基于图的神经网络的实现。
这篇教程的目的是:
- 了解DGL如何从高层次进行图形计算。
- 在DGL中训练一个简单的图神经网络以对图中的节点进行分类。
在本教程的最后,我们希望您对DGL的工作方式有一个简要的了解。
本教程假定您对pytorch基本熟悉。
Tutorial problem description
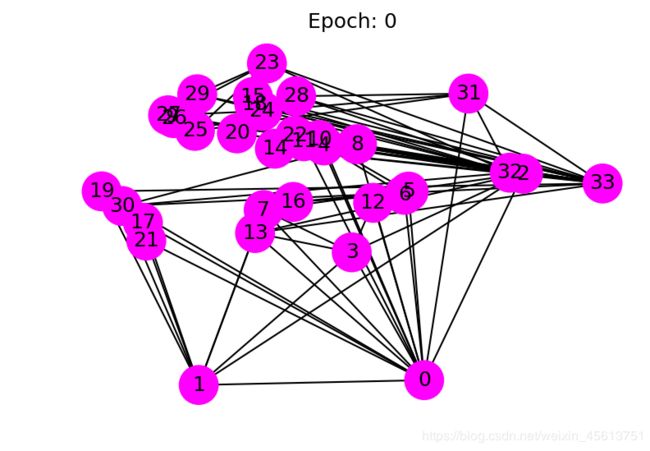
本教程基于“Zachary’s karate club”问题。Karate club是一个社交网络,包括34个成员,并在俱乐部外互动的成员之间建立成对链接。 俱乐部随后分为两个社区,由教员(节点0)和俱乐部主席(节点33)领导。 网络以如下方式可视化,并带有表示社区的颜色:

任务是预测给定社交网络本身每个成员倾向于加入哪一侧(0或33)。
Step 1: 在DGL中创建图形
如下创建Zachary’s karate clu的关系网络图:
import dgl
def build_karate_club_graph():
g = dgl.DGLGraph()
# 在图中添加34个节点,分别标记为0至333
g.add_nodes(34)
# 所有78条边组成一个元组列表
edge_list = [(1, 0), (2, 0), (2, 1), (3, 0), (3, 1), (3, 2),
(4, 0), (5, 0), (6, 0), (6, 4), (6, 5), (7, 0), (7, 1),
(7, 2), (7, 3), (8, 0), (8, 2), (9, 2), (10, 0), (10, 4),
(10, 5), (11, 0), (12, 0), (12, 3), (13, 0), (13, 1), (13, 2),
(13, 3), (16, 5), (16, 6), (17, 0), (17, 1), (19, 0), (19, 1),
(21, 0), (21, 1), (25, 23), (25, 24), (27, 2), (27, 23),
(27, 24), (28, 2), (29, 23), (29, 26), (30, 1), (30, 8),
(31, 0), (31, 24), (31, 25), (31, 28), (32, 2), (32, 8),
(32, 14), (32, 15), (32, 18), (32, 20), (32, 22), (32, 23),
(32, 29), (32, 30), (32, 31), (33, 8), (33, 9), (33, 13),
(33, 14), (33, 15), (33, 18), (33, 19), (33, 20), (33, 22),
(33, 23), (33, 26), (33, 27), (33, 28), (33, 29), (33, 30),
(33, 31), (33, 32)]
#为边添加两个列表:src and dst
src, dst = tuple(zip(*edge_list))
g.add_edges(src, dst)
# 边是有方向的,并使他们双向
g.add_edges(dst, src)
return g
在我们新建的图形中打印出节点和边的数量:
G = build_karate_club_graph() print('We have %d nodes.' % G.number_of_nodes()) print('We have %d edges.' % G.number_of_edges())
out:
We have 34 nodes.
We have 156 edges.
通过将其转换为networkx图来可视化该图:
import networkx as nx
# 由于实际图形是无向的,因此我们去掉边的方向,以达到可视化的目的
nx_G = G.to_networkx().to_undirected()
# 为了图更加美观,我们使用Kamada-Kawaii layout
pos = nx.kamada_kawai_layout(nx_G)
nx.draw(nx_G, pos, with_labels=True, node_color=[[.7, .7, .7]])
也可以不使用Kamada-Kawaii layout,结果如下所示
import networkx as nx
nx_G = G.to_networkx().to_undirected()
nx.draw(nx_G, with_labels=True, node_color=[[.7, .7, .7]])
Step2:将特征分配给节点或边
图神经网络将特征与节点和边关联以进行训练。在我们的分类例子中,我们为每一个节点分配一个one-hot向量:节点 v i v_i vi的特征向量是: [ 0 , … , 1 , … , 0 ] [0,\ldots,1,\dots,0] [0,…,1,…,0],在特征向量,第 i i i个位置为1。
在DGL中,您可以通过一个特征张量为所有的节点同时添加特征,该张量可以沿着第一维批量处理节点要素。 下面的代码为所有节点添加了一键式功能:
import torch
G.ndata['feat'] = torch.eye(34)
print(torch.eye(34))
out:
tensor([[1., 0., 0., ..., 0., 0., 0.],
[0., 1., 0., ..., 0., 0., 0.],
[0., 0., 1., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 1., 0., 0.],
[0., 0., 0., ..., 0., 1., 0.],
[0., 0., 0., ..., 0., 0., 1.]])
打印出部分节点特征来验证。
# 打印出label为2的节点的特征
print(G.nodes[2].data['feat'])
# 打印出label为10和11的节点的特征
print(G.nodes[[10, 11]].data['feat'])
out:
tensor([[0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]])
tensor([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0.,0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]])
Step 3: 定义一个图卷积神经网络(GCN)
要执行节点分类,请使用由Kipf and Welling开发的图卷积网络(GCN)。 这是GCN框架的最简单定义。 我们建议您阅读原始文章以获取更多详细信息。
- 在第 l l l层中,对于一个确定的 v i l v_i^l vil会有一个特征向量 h i l h_i^l hil
- GCN的每一层都尝试将 v v v的临近节点 u i l u_i^{l} uil的特征聚合到 v i l + 1 v_i^{l+1} vil+1( v v v在下一层中的表示)。 随后还会有具有某些非线性的仿射变换。
GCN的上述定义适用于message-passing 范例:每个节点将使用从相邻节点发送的信息来更新其自身的功能。 图形演示如下:

下面,我们展示了如何在DGL中实现GCN层。
import torch.nn as nn
import torch.nn.functional as F
# 定义 message function and reduce function
# NOTE: 在本教程中,我们将忽略GCN的规范化常数c_ij。
def gcn_message(edges):
# 该函数批量处理边
# This computes a (batch of) message called 'msg' using the source node's feature 'h'.
return {'msg' : edges.src['h']}#edges.src.data指的是获取边出发节点的‘h’属性信息
def gcn_reduce(nodes):
# 该函数批量处理节点
# This computes the new 'h' features by summing received 'msg' in each node's mailbox.
return {'h' : torch.sum(nodes.mailbox['msg'], dim=1)}#表示将附近有连接的节点的‘msg’属性数据按照'dim=1'进行加和,成为该节点新的‘h’属性数据
# 定义GCNLayer模块
class GCNLayer(nn.Module):
def __init__(self, in_feats, out_feats):
super(GCNLayer, self).__init__()
self.linear = nn.Linear(in_feats, out_feats)
def forward(self, g, inputs):
# g 是图(graph) 并且 inputs 是输入的节点特征
# 首先设置边缘特征
g.ndata['h'] = inputs
# 触发在所有边上传递信息
g.send(g.edges(), gcn_message)
# 触发在所有边上聚集信息
g.recv(g.nodes(), gcn_reduce)
# 提取边缘特征的结果
h = g.ndata.pop('h')
# 进行线性变换
return self.linear(h)
一般来说,节点通过“message”函数传递信息,然后通过“reduce”函数进行数据聚合。
定义一个包含两个GCN layers的GCN模型:
# 定义一个包含两个GCN layers的GCN模型
class GCN(nn.Module):
def __init__(self, in_feats, hidden_size, num_classes):
super(GCN, self).__init__()
self.gcn1 = GCNLayer(in_feats, hidden_size)
self.gcn2 = GCNLayer(hidden_size, num_classes)
def forward(self, g, inputs):
h = self.gcn1(g, inputs)
h = torch.relu(h)
h = self.gcn2(g, h)
return h
# 第一层将大小为34的输入特征转换为隐藏的大小为5。
# 第二层将隐藏层转换为大小为2的输出特征,对应Karate club中的两个组。
net = GCN(34, 5, 2)
Step 4:数据准备和初始化
我们使用one-hot向量来初始化节点特征。 由于这是半监督设置,因此仅为教练(node 0)和俱乐部主席(node 33)分配标签。 该实现如下:
Step 5:训练然后可视化
训练循环和其他的Pytorch 模型相同。我们(1)创建一个优化函数,(2)将输入提供给模型,(3)计算损失,(4)使用autograd优化模型。
optimizer = torch.optim.Adam(net.parameters(), lr=0.01)
all_logits = []
for epoch in range(30):
logits = net(G, inputs)
# 我们保存the logits以便于接下来可视化
all_logits.append(logits.detach())
logp = F.log_softmax(logits, 1)
# 我们仅仅为标记过的节点计算loss
loss = F.nll_loss(logp[labeled_nodes], labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
print('Epoch %d | Loss: %.4f' % (epoch, loss.item()))
out:
Epoch 0 | Loss: 0.6533
Epoch 1 | Loss: 0.3839
Epoch 2 | Loss: 0.2743
Epoch 3 | Loss: 0.2123
Epoch 4 | Loss: 0.1558
Epoch 5 | Loss: 0.1077
Epoch 6 | Loss: 0.0718
Epoch 7 | Loss: 0.0483
Epoch 8 | Loss: 0.0337
Epoch 9 | Loss: 0.0240
Epoch 10 | Loss: 0.0179
Epoch 11 | Loss: 0.0137
Epoch 12 | Loss: 0.0108
Epoch 13 | Loss: 0.0087
Epoch 14 | Loss: 0.0071
Epoch 15 | Loss: 0.0059
Epoch 16 | Loss: 0.0049
Epoch 17 | Loss: 0.0041
Epoch 18 | Loss: 0.0035
Epoch 19 | Loss: 0.0030
Epoch 20 | Loss: 0.0026
Epoch 21 | Loss: 0.0022
Epoch 22 | Loss: 0.0019
Epoch 23 | Loss: 0.0017
Epoch 24 | Loss: 0.0015
Epoch 25 | Loss: 0.0013
Epoch 26 | Loss: 0.0012
Epoch 27 | Loss: 0.0010
Epoch 28 | Loss: 0.0009
Epoch 29 | Loss: 0.0009
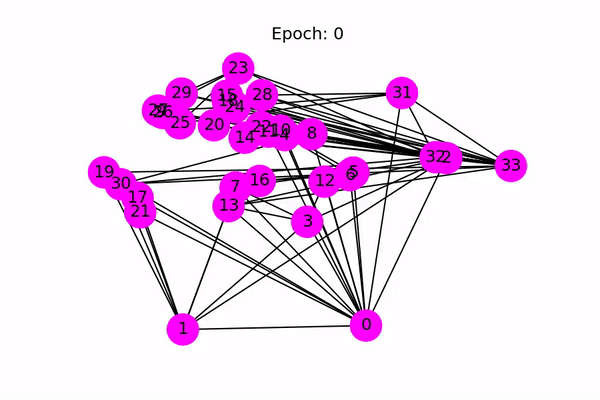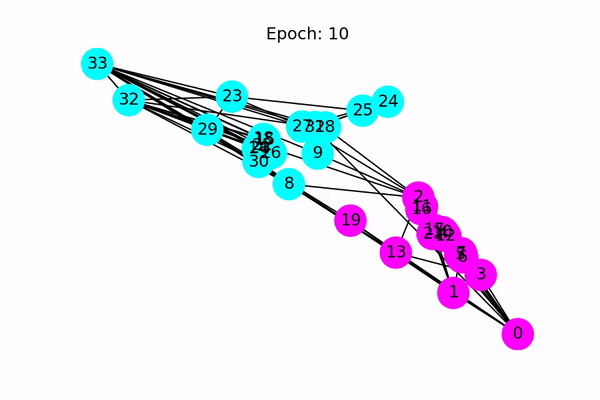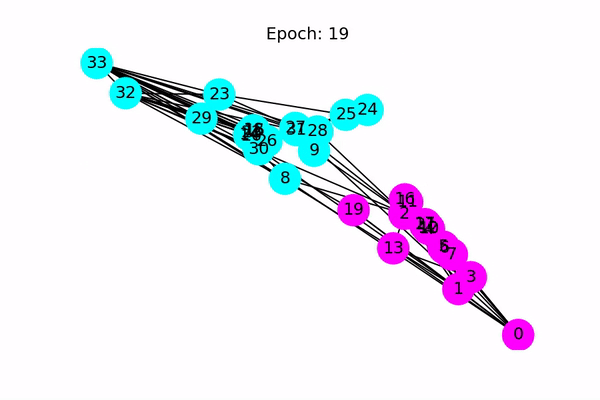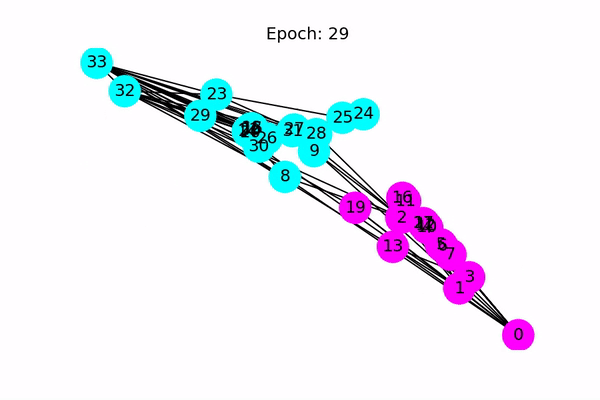
这是一个很有趣的例子,因此甚至没有验证或测试集。 相反,由于模型为每个节点生成大小为2的输出特征,因此我们可以通过在2D空间中绘制输出特征来可视化。 下面的代码使训练过程从最初的猜测(根本没有正确分类节点)到最终的结果(线性可分离节点)动画化。
import matplotlib.animation as animation
import matplotlib.pyplot as plt
def draw(i):
cls1color = '#00FFFF'
cls2color = '#FF00FF'
pos = {}
colors = []
for v in range(34):
pos[v] = all_logits[i][v].numpy()
cls = pos[v].argmax()
colors.append(cls1color if cls else cls2color)
ax.cla()
ax.axis('off')
ax.set_title('Epoch: %d' % i)
nx.draw_networkx(nx_G.to_undirected(), pos, node_color=colors,
with_labels=True, node_size=300, ax=ax)
fig = plt.figure(dpi=150)
fig.clf()
ax = fig.subplots()
draw(0) # draw the prediction of the first epoch
plt.close()
ani = animation.FuncAnimation(fig, draw, frames=len(all_logits), interval=200)
Next steps
在下一个教程中,我们将介绍DGL的更多基础知识,例如读写notes/edges功能。
Total running time of the script: ( 0 minutes 0.485 seconds)
下载源码:1_first.py
下载源码:1_first.ipynb