LeetCode 190周赛T4. 两个子序列的最大点积

题目

给你两个数组 nums1 和 nums2 。

请你返回 nums1 和 nums2 中两个长度相同的 非空 子序列的最大点积。

数组的非空子序列是通过删除原数组中某些元素（可能一个也不删除）后剩余数字组成的序列，但不能改变数字间相对顺序。比方说，[2,3,5] 是 [1,2,3,4,5] 的一个子序列而 [1,5,3] 不是。

示例 1：

输入：nums1 = [2,1,-2,5], nums2 = [3,0,-6]
输出：18
解释：从 nums1 中得到子序列 [2,-2] ，从 nums2 中得到子序列 [3,-6] 。
它们的点积为 (2*3 + (-2)*(-6)) = 18 。
示例 2：

输入：nums1 = [3,-2], nums2 = [2,-6,7]
输出：21
解释：从 nums1 中得到子序列 [3] ，从 nums2 中得到子序列 [7] 。
它们的点积为 (3*7) = 21 。
示例 3：

输入：nums1 = [-1,-1], nums2 = [1,1]
输出：-1
解释：从 nums1 中得到子序列 [-1] ，从 nums2 中得到子序列 [1] 。
它们的点积为 -1 。
提示：
1 <= nums1.length, nums2.length <= 500
-1000 <= nums1[i], nums2[i] <= 100

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/contest/weekly-contest-190/problems/max-dot-product-of-two-subsequences/
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
————————————————

题解

一道十分经典的dp题目，为什么第一眼就能想到dp呢？首先，我们可以排除爆搜加优化，之后我们就得思考在我们一步一步计算的过程中，一定会产生非常多的无用功，所以我们每次都得保存下当前最大的点积。
由于dp问题的本质其实就是当前状态和已知状态之间的关系，变换得到当前值，所以先来考虑状态方程，对于dp[i][j]的可能最大值的情况有几种呢？
1.nums1[i] 我们不使用它，那么此时就有 dp[i][j] = dp[i-1][j]
2.nums2[j] 我们不使用它，那么此时就有 dp[i][j] = dp[i][j-1]
3.nums1[i],nums2[j] 我们都使用，那么最后一个点积就一定是nums1[i]*nums2[j]了，
此时dp[i][j] = dp[i-1][j-1] + nums1[i]*nums2[j]
4.由于状态三中 dp[i-1][j-1]也有可能为负数，所以我们可以选择不使用，则dp[i][j] = nums1[i]*nums2[j]

好了！只需要这四种状态，那么初始化的值呢？我们应该把dp[0][j],dp[i][0]全部初始化为负无穷，因为不可以使num1或nums2选取的元素长度为0.
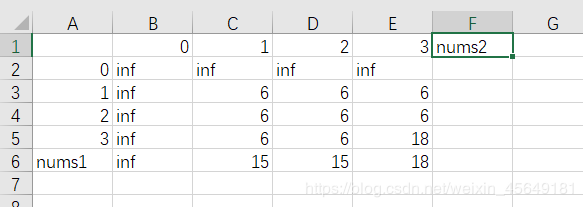
这是推演出来的表格，在解决dp问题时强烈建议手动推算，这样将更容易发现规律，利用已知的状态信息。

class Solution {
    public int maxDotProduct(int[] nums1, int[] nums2) {
    	int n1 = nums1.length;
    	int n2 = nums2.length;
    	int[][] dp = new int[n1+1][n2+1];
        for(int i = 0; i <= n1; i ++){
            dp[i][0] = Integer.MIN_VALUE/2;
        }
        for(int j = 0; j <= n2; j ++){
            dp[0][j] = Integer.MIN_VALUE/2;
        }
    	for(int i = 1; i <= n1; i ++) {
    		for(int j = 1; j <= n2; j ++) {
    			dp[i][j] = Math.max(
    			Math.max(dp[i-1][j] , nums1[i-1]*nums2[j-1]),
    			Math.max(dp[i-1][j-1]+nums1[i-1]*nums2[j-1] ,dp[i][j-1]) 
    			);
    		}
    	}
    	return dp[n1][n2];
    }
}