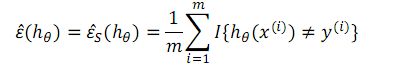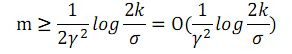斯坦福大学公开课机器学习课程(Andrew Ng)九经验风险最小化
课程概述:
1.偏差/方差(Bias/variance)
2.经验风险最小化(Empirical Risk Minization,ERM)
3.联合界引理与Hoeffding不等式
4.一致收敛(Uniform Convergence)
一、偏差/方差
偏差与方差对应的仍然是过拟合与欠拟合的问题,本篇主要解决的问题就在于构建一个模型,对何时出现过拟合和欠拟合进行说明。
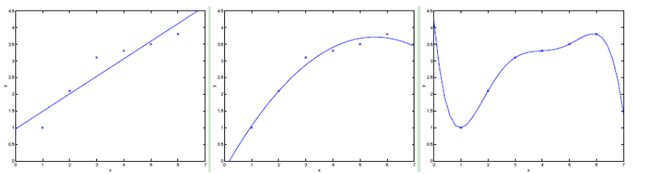
关于过拟合与欠拟合的问题,前面已经讲过,这里在稍微说一下,如下图:
上图中,左图为欠拟合,即没有很好的拟合所有的数据,有很大的泛化误差,这种情况对应于高偏差;
中间的图为较好的拟合;
右图为过拟合,即对实验数据集合的太好,这样当换一组数据时就可能有较大的误差,即不具有一般性,这种情况对应于高方差。
简而言之,欠拟合对应了高偏差,过拟合对应高方差。
二、经验风险最小化(Experience Risk Minimization,ERM)
首先,我们定义数据集:
其中![]() 是i.i.d(独立同分布变量)。y ∈ {0,1}。
是i.i.d(独立同分布变量)。y ∈ {0,1}。
![]()
由定义可知,![]() 的输出只能为0 或者 1。
的输出只能为0 或者 1。
这个模型和logistic回归比较像,当z满足某个条件时。g(z)取0或1。
定义训练误差:
这个公式的含义为被错误分类的样本占总体样本的比例,后面的累加为错误样本数,除以总体样本m即为所占比例。
那么经验误差最小化即为:
即选择使训练误差最小的参数。
对于 ERM 来说,因为它是非凸的,故而一般的算法无法优化它,因为它是 NP 的。但值得注意的是,logistic回归与 SVM都是这种方法的凸性近似。
再看另外一种等价的 ERM的定义,假设模型集合:
这是一个假设模型集合,每改变参数时,就会选取一个假设模型,logistic回归可以从中选取一个假设作为结果。
其中,ℎ为分类模型,输出为 0,1。其训练误差的定义为:
而我们关心的泛化能力(一般误差,即再取一个新样本时分类错误的概率)的定义为:
![]()
接下来的任务,是证明最优化 ERM能带来较小的泛化误差。首先,我们引入两个引理。
三、联合界引理与Hoeffding不等式
首先是联合界定理,令A1,A2,…,Ak是k 个事件,这k 个事件可以相互独立也可以不相互独立,那么我们会得到:
![]()
该定理可以用文氏图来说明:
即各个事件并集的概率一定小于等于这些事件概率的和。
接下来是Hoeffding不等式引理, 令Z1,Z2,…,Zm为 m个独立同分布(i.i.d)变量,它们都服从Bernoulli分布,即: ![]()
那么Hoeffding不等式的定义即为对于任意的固定数值γ > 0,存在:
![]()
这个式子的含义为预测值与真实值的差大于γ的概率小于右面的式子。
如下图中的左右两个阴影部分(即犯错误的部分),它们的上界由上个不等式的右式给出。
当样本数量增大时,高斯函数会更为凸起,两边的概率密度会减小,这就意味着,随着样本数量的增加,我们对参数的估计将越来越逼近真实值。
四、一致收敛
我们使用ERM的第二种定义来证明该定理。首先推导当模型集合是有限集合的时候成立的定理。
定义模型集合为: ![]()
首先,我们证明对于所有的 h 来说,![]() (训练误差)都是
(训练误差)都是![]() (一般误差)的一个很好的估计;其次,我们证明使用ERM方法得到的ℎ ̂的一般误差是有上限的。
(一般误差)的一个很好的估计;其次,我们证明使用ERM方法得到的ℎ ̂的一般误差是有上限的。
证明第一个:
从模型集合中任意选择一个假设 hj,那么会有: ![]()
而训练误差的定义是m个I(Zi = 1)之和,即为m个服从Bernoulli分布的随机变量之和,
而根据Hoeffding不等式引理,得到:
由此,第一个定理得证。
证明第二个:
令事件Aj为![]() ,那么有
,那么有
那么可以推导出至少存在一个假设 hi,使![]() 成立的概率为:
成立的概率为:
该式即为一致收敛定理,它的意义在于,至少有1 − 2kexp(−2γ^2m)的概率,使得模型集合中的所有假设,其泛化误差都在训练误差的γ范围内。
一致收敛的推论
在一致收敛中,有三个参数,m,γ,概率。这三个参数是相互关联的,我们可以通过固定其中两个,来推出第三个。其中固定m,γ来求概率已经得出了,下面依次对另外两种参数关联进行说明。
第一个,给定γ和σ > 0,需要多少样本,可以保证在至少有1-σ的概率,使得泛化错误率在训练错误率的γ范围内?
对下式进行求解即得到答案: ![]()
得到:
这个推论的意义为,一个算法或者模型要达到一个确定的性能时,需要的样本数目。也称为算法的样本复杂度。
第二个,给定m和σ > 0,泛化错误率会落在训练错误率的什么范围内?
下面我们看看在在一致收敛成立的情况下,我们通过 ERM 方法得到的假设ℎ ̂的泛化能力到底如何?
首先,定义: ![]()
即ℎ* 为ℋ中泛化误差最小的假设。
我们可以推出: ![]()
其中,第一个不等号成立是一致收敛定理的应用;第二个不等号成立是ℎ ̂的定义决定,其本身为训练误差最小的假设;第三个不等号成立仍然是一致收敛定理的应用。
这表明,在一致收敛定理成立的时候,通过ERM得到的训练误差最小的假设在泛化能力上至多比泛化能力最好的假设差2γ。
将这些推论综合一下,我们得到一个定理:
令|ℋ| = k,给定m和σ > 0,那么至少有1-σ的概率能够成立如下公式: 
该定理反映了偏差和方差的权衡。可以想象,当选择一个复杂的模型假设时, |ℋ| = k会变大,导致不等式后的第二项变大,意味着方差变大;但是第一项却会变小,因为使用一个更加大的模型集合ℋ意味着可供选择的假设变多了,在多的那部分中可能有比原来还要小的模型,这样偏差就会变小。选择一个最优值,使得偏差与方差之和最小,才能得到一个好的模型。
同样的,该定理还有另外形式的推论:
令|ℋ| = k,给定γ和σ > 0,那么至少有 1-σ的概率使
![]()
成立的前提是:
参考:
斯坦福ML公开课笔记