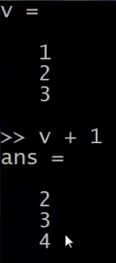吴恩达机器学习笔记(1-5周)

---

title: 吴恩达机器学习笔记(1-5周)
date: 2019-12-04 09:28:03
categories: 人工智能
tags:

• nlp
  cover: https://www.github.com/OneJane/blog/raw/master/小书匠/82a490a419fe375d72125e422ed31adb_hd.jpg

---

吴恩达机器学习笔记

引言

监督学习

参考视频: 1 - 3 - Supervised Learning (12 min).mkv
我们用一个例子介绍什么是监督学习把正式的定义放在后面介绍。假如说你想预测房价。

前阵子，一个学生从波特兰俄勒冈州的研究所收集了一些房价的数据。你把这些数据画出来，看起来是这个样子：横轴表示房子的面积，单位是平方英尺，纵轴表示房价，单位是千美元。那基于这组数据，假如你有一个朋友，他有一套750平方英尺房子，现在他希望把房子卖掉，他想知道这房子能卖多少钱。

那么关于这个问题，机器学习算法将会怎么帮助你呢？

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hf2WwLkW-1575445908518)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575423614245.png)]

我们应用学习算法，可以在这组数据中画一条直线，或者换句话说，拟合一条直线，根据这条线我们可以推测出，这套房子可能卖$150,000，当然这不是唯一的算法。可能还有更好的，比如我们不用直线拟合这些数据，用二次方程去拟合可能效果会更好。根据二次方程的曲线，我们可以从这个点推测出，这套房子能卖接近$200,000。稍后我们将讨论如何选择学习算法，如何决定用直线还是二次方程来拟合。两个方案中有一个能让你朋友的房子出售得更合理。这些都是学习算法里面很好的例子。以上就是监督学习的例子。

可以看出，监督学习指的就是我们给学习算法一个数据集。这个数据集由“正确答案”组成。在房价的例子中，我们给了一系列房子的数据，我们给定数据集中每个样本的正确价格，即它们实际的售价然后运用学习算法，算出更多的正确答案。比如你朋友那个新房子的价格。用术语来讲，这叫做回归问题。我们试着推测出一个连续值的结果，即房子的价格。

一般房子的价格会记到美分，所以房价实际上是一系列离散的值，但是我们通常又把房价看成实数，看成是标量，所以又把它看成一个连续的数值。

回归这个词的意思是，我们在试着推测出这一系列连续值属性。

我再举另外一个监督学习的例子。我和一些朋友之前研究过这个。假设说你想通过查看病历来推测乳腺癌良性与否，假如有人检测出乳腺肿瘤，恶性肿瘤有害并且十分危险，而良性的肿瘤危害就没那么大，所以人们显然会很在意这个问题。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SJ2VJkY9-1575445908519)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575423705880.png)]

让我们来看一组数据：这个数据集中，横轴表示肿瘤的大小，纵轴上，我标出1和0表示是或者不是恶性肿瘤。我们之前见过的肿瘤，如果是恶性则记为1，不是恶性，或者说良性记为0。

我有5个良性肿瘤样本，在1的位置有5个恶性肿瘤样本。现在我们有一个朋友很不幸检查出乳腺肿瘤。假设说她的肿瘤大概这么大，那么机器学习的问题就在于，你能否估算出肿瘤是恶性的或是良性的概率。用术语来讲，这是一个分类问题。

分类指的是，我们试着推测出离散的输出值：0或1良性或恶性，而事实上在分类问题中，输出可能不止两个值。比如说可能有三种乳腺癌，所以你希望预测离散输出0、1、2、3。0 代表良性，1 表示第1类乳腺癌，2表示第2类癌症，3表示第3类，但这也是分类问题。

因为这几个离散的输出分别对应良性，第一类第二类或者第三类癌症，在分类问题中我们可以用另一种方式绘制这些数据点。

现在我用不同的符号来表示这些数据。既然我们把肿瘤的尺寸看做区分恶性或良性的特征，那么我可以这么画，我用不同的符号来表示良性和恶性肿瘤。或者说是负样本和正样本现在我们不全部画X，良性的肿瘤改成用 O 表示，恶性的继续用 X 表示。来预测肿瘤的恶性与否。

在其它一些机器学习问题中，可能会遇到不止一种特征。举个例子，我们不仅知道肿瘤的尺寸，还知道对应患者的年龄。在其他机器学习问题中，我们通常有更多的特征，我朋友研究这个问题时，通常采用这些特征，比如肿块密度，肿瘤细胞尺寸的一致性和形状的一致性等等，还有一些其他的特征。这就是我们即将学到最有趣的学习算法之一。

那种算法不仅能处理2种3种或5种特征，即使有无限多种特征都可以处理。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-i2wAShWV-1575445908519)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575423772270.png)]

上图中，我列举了总共5种不同的特征，坐标轴上的两种和右边的3种，但是在一些学习问题中，你希望不只用3种或5种特征。相反，你想用无限多种特征，好让你的算法可以利用大量的特征，或者说线索来做推测。那你怎么处理无限多个特征，甚至怎么存储这些特征都存在问题，你电脑的内存肯定不够用。我们以后会讲一个算法，叫支持向量机，里面有一个巧妙的数学技巧，能让计算机处理无限多个特征。 想象一下，我没有写下这两种和右边的三种特征，而是在一个无限长的列表里面，一直写一直写不停的写，写下无限多个特征，事实上，我们能用算法来处理它们。

现在来回顾一下，这节课我们介绍了监督学习。其基本思想是，我们数据集中的每个样本都有相应的“正确答案”。再根据这些样本作出预测，就像房子和肿瘤的例子中做的那样。我们还介绍了回归问题，即通过回归来推出一个连续的输出，之后我们介绍了分类问题，其目标是推出一组离散的结果。

现在来个小测验：假设你经营着一家公司，你想开发学习算法来处理这两个问题：

1. 你有一大批同样的货物，想象一下，你有上千件一模一样的货物等待出售，这时你想预测接下来的三个月能卖多少件？

2. 你有许多客户，这时你想写一个软件来检验每一个用户的账户。对于每一个账户，你要判断它们是否曾经被盗过？

那这两个问题，它们属于分类问题、还是回归问题?

问题一是一个回归问题，因为你知道，如果我有数千件货物，我会把它看成一个实数，一个连续的值。因此卖出的物品数，也是一个连续的值。

问题二是一个分类问题，因为我会把预测的值，用 0 来表示账户未被盗，用 1 表示账户曾经被盗过。所以我们根据账号是否被盗过，把它们定为0 或 1，然后用算法推测一个账号是 0 还是 1，因为只有少数的离散值，所以我把它归为分类问题。

以上就是监督学习的内容。

无监督学习

参考视频: 1 - 4 - Unsupervised Learning (14 min).mkv
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Wra4JAqB-1575445908520)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575423900529.png)]

上个视频中，已经介绍了监督学习。回想当时的数据集，如图表所示，这个数据集中每条数据都已经标明是阴性或阳性，即是良性或恶性肿瘤。所以，对于监督学习里的每条数据，我们已经清楚地知道，训练集对应的正确答案，是良性或恶性了。

在无监督学习中，我们已知的数据。看上去有点不一样，不同于监督学习的数据的样子，即无监督学习中没有任何的标签或者是有相同的标签或者就是没标签。所以我们已知数据集，却不知如何处理，也未告知每个数据点是什么。别的都不知道，就是一个数据集。你能从数据中找到某种结构吗？针对数据集，无监督学习就能判断出数据有两个不同的聚集簇。这是一个，那是另一个，二者不同。是的，无监督学习算法可能会把这些数据分成两个不同的簇。所以叫做聚类算法。事实证明，它能被用在很多地方。

聚类应用的一个例子就是在谷歌新闻中。如果你以前从来没见过它，你可以到这个URL网址news.google.com去看看。谷歌新闻每天都在，收集非常多，非常多的网络的新闻内容。它再将这些新闻分组，组成有关联的新闻。所以谷歌新闻做的就是搜索非常多的新闻事件，自动地把它们聚类到一起。所以，这些新闻事件全是同一主题的，所以显示到一起。

事实证明，聚类算法和无监督学习算法同样还用在很多其它的问题上。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-b7O6JtZX-1575445908521)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575423980984.png)]

其中就有基因学的理解应用。一个DNA微观数据的例子。基本思想是输入一组不同个体，对其中的每个个体，你要分析出它们是否有一个特定的基因。技术上，你要分析多少特定基因已经表达。所以这些颜色，红，绿，灰等等颜色，这些颜色展示了相应的程度，即不同的个体是否有着一个特定的基因。你能做的就是运行一个聚类算法，把个体聚类到不同的类或不同类型的组（人）……

所以这个就是无监督学习，因为我们没有提前告知算法一些信息，比如，这是第一类的人，那些是第二类的人，还有第三类，等等。我们只是说，是的，这是有一堆数据。我不知道数据里面有什么。我不知道谁是什么类型。我甚至不知道人们有哪些不同的类型，这些类型又是什么。但你能自动地找到数据中的结构吗？就是说你要自动地聚类那些个体到各个类，我没法提前知道哪些是哪些。因为我们没有给算法正确答案来回应数据集中的数据，所以这就是无监督学习。

无监督学习或聚集有着大量的应用。它用于组织大型计算机集群。我有些朋友在大数据中心工作，那里有大型的计算机集群，他们想解决什么样的机器易于协同地工作，如果你能够让那些机器协同工作，你就能让你的数据中心工作得更高效。第二种应用就是社交网络的分析。所以已知你朋友的信息，比如你经常发email的，或是你Facebook的朋友、谷歌+ 圈子的朋友，我们能否自动地给出朋友的分组呢？即每组里的人们彼此都熟识，认识组里的所有人？还有市场分割。许多公司有大型的数据库，存储消费者信息。所以，你能检索这些顾客数据集，自动地发现市场分类，并自动地把顾客划分到不同的细分市场中，你才能自动并更有效地销售或不同的细分市场一起进行销售。这也是无监督学习，因为我们拥有所有的顾客数据，但我们没有提前知道是什么的细分市场，以及分别有哪些我们数据集中的顾客。我们不知道谁是在一号细分市场，谁在二号市场，等等。那我们就必须让算法从数据中发现这一切。最后，无监督学习也可用于天文数据分析，这些聚类算法给出了令人惊讶、有趣、有用的理论，解释了星系是如何诞生的。这些都是聚类的例子，聚类只是无监督学习中的一种。

我现在告诉你们另一种。我先来介绍鸡尾酒宴问题。嗯，你参加过鸡尾酒宴吧？你可以想像下，有个宴会房间里满是人，全部坐着，都在聊天，这么多人同时在聊天，声音彼此重叠，因为每个人都在说话，同一时间都在说话，你几乎听不到你面前那人的声音。所以，可能在一个这样的鸡尾酒宴中的两个人，他俩同时都在说话，假设现在是在个有些小的鸡尾酒宴中。我们放两个麦克风在房间中，因为这些麦克风在两个地方，离说话人的距离不同每个麦克风记录下不同的声音，虽然是同样的两个说话人。听起来像是两份录音被叠加到一起，或是被归结到一起，产生了我们现在的这些录音。另外，这个算法还会区分出两个音频资源，这两个可以合成或合并成之前的录音，实际上，鸡尾酒算法的第一个输出结果是：

1，2，3，4，5，6，7，8，9，10,

所以，已经把英语的声音从录音中分离出来了。

第二个输出是这样：

1，2，3，4，5，6，7，8，9，10。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-U1laxbOf-1575445908521)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575424111930.png)]

看看这个无监督学习算法，实现这个得要多么的复杂，是吧？它似乎是这样，为了构建这个应用，完成这个音频处理似乎需要你去写大量的代码或链接到一堆的合成器JAVA库，处理音频的库，看上去绝对是个复杂的程序，去完成这个从音频中分离出音频。事实上，这个算法对应你刚才知道的那个问题的算法可以就用一行代码来完成。

就是这里展示的代码：[W,s,v] = svd((repmat(sum(x.*x,1),size(x,1),1).*x)*x');

研究人员花费了大量时间才最终实现这行代码。我不是说这个是简单的问题，但它证明了，当你使用正确的编程环境，许多学习算法是相当短的程序。所以，这也是为什么在本课中，我们打算使用Octave编程环境。Octave,是免费的开源软件，使用一个像Octave或Matlab的工具，许多学习算法变得只有几行代码就可实现。

后面，我会教你们一点关于如何使用Octave的知识，你就可以用Octave来实现一些算法了。或者，如果你有Matlab（盗版？），你也可以用Matlab。事实上，在硅谷里，对大量机器学习算法，我们第一步就是建原型，在Octave建软件原型，因为软件在Octave中可以令人难以置信地、快速地实现这些学习算法。这里的这些函数比如SVM（支持向量机）函数，奇异值分解，Octave里已经建好了。如果你试图完成这个工作，但借助C++或JAVA的话，你会需要很多很多行的代码，并链接复杂的C++或Java库。所以，你可以实现这些算法，借助C++或Java或Python，它只是用这些语言来实现会更加复杂。(编者注：这个是当时的情况，现在Python变主流了)

我已经见到，在我教机器学习将近十年后的现在，发现，学习可以更加高速，如果使用Octave作为编程环境，如果使用Octave作为学习工具，以及作为原型工具，它会让你对学习算法的学习和建原型快上许多。

事实上，许多人在大硅谷的公司里做的其实就是，使用一种工具像Octave来做第一步的学习算法的原型搭建，只有在你已经让它工作后，你才移植它到C++ 或Java或别的语言。事实证明，这样做通常可以让你的算法运行得比直接用C++ 实现更快，所以，我知道，作为一名指导者，我必须说“相信我”，但对你们中从未使用过Octave这种编程环境的人，我还是要告诉你们这一点一定要相信我，我想，对你们而言，我认为你们的时间，你们的开发时间是最有价值的资源。我已经见过很多人这样做了，我把你看作是机器学习研究员，或机器学习开发人员，想更加高产的话，你要学会使用这个原型工具，开始使用Octave。

我们介绍了无监督学习，它是学习策略，交给算法大量的数据，并让算法为我们从数据中找出某种结构。

好的，希望你们还记得垃圾邮件问题。如果你有标记好的数据，区别好是垃圾还是非垃圾邮件，我们把这个当作监督学习问题。

新闻事件分类的例子，就是那个谷歌新闻的例子，我们在本视频中有见到了，我们看到，可以用一个聚类算法来聚类这些文章到一起，所以是无监督学习。

细分市场的例子，我在更早一点的时间讲过，你可以当作无监督学习问题，因为我只是拿到算法数据，再让算法去自动地发现细分市场。

最后一个例子，糖尿病，这个其实就像是我们的乳腺癌，上个视频里的。只是替换了好、坏肿瘤，良性、恶性肿瘤，我们改用糖尿病或没病。所以我们把这个当作监督学习，我们能够解决它，作为一个监督学习问题，就像我们在乳腺癌数据中做的一样。

单变量线性回归(Linear Regression with One Variable)

模型表示

参考视频: 2 - 1 - Model Representation (8 min).mkv

让我们通过一个例子来开始：这个例子是预测住房价格的，我们要使用一个数据集，数据集包含俄勒冈州波特兰市的住房价格。在这里，我要根据不同房屋尺寸所售出的价格，画出我的数据集。比方说，如果你朋友的房子是1250平方尺大小，你要告诉他们这房子能卖多少钱。那么，你可以做的一件事就是构建一个模型，也许是条直线，从这个数据模型上来看，也许你可以告诉你的朋友，他能以大约220000(美元)左右的价格卖掉这个房子。这就是监督学习算法的一个例子。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oIhAMHiF-1575445908522)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575424452903.png)]

它被称作监督学习是因为对于每个数据来说，我们给出了“正确的答案”，即告诉我们：根据我们的数据来说，房子实际的价格是多少，而且，更具体来说，这是一个回归问题。回归一词指的是，我们根据之前的数据预测出一个准确的输出值，对于这个例子就是价格，同时，还有另一种最常见的监督学习方式，叫做分类问题，当我们想要预测离散的输出值，例如，我们正在寻找癌症肿瘤，并想要确定肿瘤是良性的还是恶性的，这就是0/1离散输出的问题。更进一步来说，在监督学习中我们有一个数据集，这个数据集被称训练集。

我将在整个课程中用小写的m来表示训练样本的数目。

以之前的房屋交易问题为例，假使我们回归问题的训练集（Training Set）如下表所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hX9M29HX-1575445908523)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575424505376.png)]

我们将要用来描述这个回归问题的标记如下:

$m$ 代表训练集中实例的数量

$x$ 代表特征/输入变量

$y$ 代表目标变量/输出变量

$\left(x,y\right)$ 代表训练集中的实例

$(x^{(i)},y^{(i)})$ 代表第$i$ 个观察实例

$h$ 代表学习算法的解决方案或函数也称为假设（hypothesis）

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Zia0GvYH-1575445908524)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575424585514.png)]

这就是一个监督学习算法的工作方式，我们可以看到这里有我们的训练集里房屋价格
我们把它喂给我们的学习算法，学习算法的工作了，然后输出一个函数，通常表示为小写 $h$ 表示。$h$ 代表hypothesis(假设)，$h$表示一个函数，输入是房屋尺寸大小，就像你朋友想出售的房屋，因此 $h$ 根据输入的 $x$值来得出 $y$ 值，$y$ 值对应房子的价格 因此，$h$ 是一个从$x$ 到 $y$ 的函数映射。

我将选择最初的使用规则$h$代表hypothesis，因而，要解决房价预测问题，我们实际上是要将训练集“喂”给我们的学习算法，进而学习得到一个假设$h$，然后将我们要预测的房屋的尺寸作为输入变量输入给$h$，预测出该房屋的交易价格作为输出变量输出为结果。那么，对于我们的房价预测问题，我们该如何表达 $h$？

一种可能的表达方式为：$h_{\theta }\left(x\right)={\theta }_0+{\theta }_{1}x$，因为只含有一个特征/输入变量，因此这样的问题叫作单变量线性回归问题。

代价函数

参考视频: 2 - 2 - Cost Function (8 min).mkv
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kf50ibOw-1575445908524)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575424646031.png)]

在线性回归中我们有一个像这样的训练集，$m$代表了训练样本的数量，比如 $m=47$。而我们的假设函数，也就是用来进行预测的函数，是这样的线性函数形式：$h_{\theta }\left(x\right)={\theta }_0+{\theta }_{1}x$。

接下来我们会引入一些术语我们现在要做的便是为我们的模型选择合适的参数（parameters）${\theta }_0$ 和 ${\theta }_1$，在房价问题这个例子中便是直线的斜率和在$y$ 轴上的截距。

我们选择的参数决定了我们得到的直线相对于我们的训练集的准确程度，模型所预测的值与训练集中实际值之间的差距（下图中蓝线所指）就是建模误差（modeling error）。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-66P79C44-1575445908525)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575424692858.png)]

我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。 即使得代价函数 $J\left({\theta }_0,{\theta }_1\right)=\frac{1}{2m}\sum _{i=1}^m{\left(h_{\theta }(x^{(i)})-y^{(i)}\right)}^2$最小。

我们绘制一个等高线图，三个坐标分别为${\theta }_0$和${\theta }_1$ 和$J({\theta }_0,{\theta }_1)$：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ySRJVewD-1575445908526)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575424716806.png)]

则可以看出在三维空间中存在一个使得$J({\theta }_0,{\theta }_1)$最小的点。

代价函数也被称作平方误差函数，有时也被称为平方误差代价函数。我们之所以要求出误差的平方和，是因为误差平方代价函数，对于大多数问题，特别是回归问题，都是一个合理的选择。还有其他的代价函数也能很好地发挥作用，但是平方误差代价函数可能是解决回归问题最常用的手段了。

在后续课程中，我们还会谈论其他的代价函数，但我们刚刚讲的选择是对于大多数线性回归问题非常合理的。

也许这个函数$J({\theta }_0,{\theta }_1)$有点抽象，可能你仍然不知道它的内涵，在接下来的几个视频里，我们要更进一步解释代价函数J的工作原理，并尝试更直观地解释它在计算什么，以及我们使用它的目的。

代价函数的直观理解

参考视频: 2 - 3 - Cost Function - Intuition I (11 min).mkv
在上一个视频中，我们给了代价函数一个数学上的定义。在这个视频里，让我们通过一些例子来获取一些直观的感受，看看代价函数到底是在干什么。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Lsd5s3zC-1575445908526)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575424876911.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-bKwrp4OY-1575445908527)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575424969202.png)]

代价函数的样子，等高线图，则可以看出在三维空间中存在一个使得$J({\theta }_0,{\theta }_1)$最小的点。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XMdF6nae-1575445908528)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575424993676.png)]

通过这些图形，我希望你能更好地理解这些代价函数$ J$所表达的值是什么样的，它们对应的假设是什么样的，以及什么样的假设对应的点，更接近于代价函数$J$的最小值。

当然，我们真正需要的是一种有效的算法，能够自动地找出这些使代价函数$J$取最小值的参数${\theta }_0$和${\theta }_1$来。

我们也不希望编个程序把这些点画出来，然后人工的方法来读出这些点的数值，这很明显不是一个好办法。我们会遇到更复杂、更高维度、更多参数的情况，而这些情况是很难画出图的，因此更无法将其可视化，因此我们真正需要的是编写程序来找出这些最小化代价函数的${\theta }_0$和${\theta }_1$的值，在下一节视频中，我们将介绍一种算法，能够自动地找出能使代价函数$J$最小化的参数${\theta }_0$和${\theta }_1$的值。

梯度下降

参考视频: 2 - 5 - Gradient Descent (11 min).mkv
梯度下降是一个用来求函数最小值的算法，我们将使用梯度下降算法来求出代价函数$J({\theta }_0,{\theta }_1)$ 的最小值。

梯度下降背后的思想是：开始时我们随机选择一个参数的组合$\left({\theta }_0,{\theta }_1,......,{\theta }_n\right)$，计算代价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到找到一个局部最小值（local minimum），因为我们并没有尝试完所有的参数组合，所以不能确定我们得到的局部最小值是否便是全局最小值（global minimum），选择不同的初始参数组合，可能会找到不同的局部最小值。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-P85FDkHH-1575445908528)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575429352272.png)]

想象一下你正站立在山的这一点上，站立在你想象的公园这座红色山上，在梯度下降算法中，我们要做的就是旋转360度，看看我们的周围，并问自己要在某个方向上，用小碎步尽快下山。这些小碎步需要朝什么方向？如果我们站在山坡上的这一点，你看一下周围，你会发现最佳的下山方向，你再看看周围，然后再一次想想，我应该从什么方向迈着小碎步下山？然后你按照自己的判断又迈出一步，重复上面的步骤，从这个新的点，你环顾四周，并决定从什么方向将会最快下山，然后又迈进了一小步，并依此类推，直到你接近局部最低点的位置。

批量梯度下降（batch gradient descent）算法的公式为：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rOmtUfkT-1575445908529)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575429392028.png)]

其中$a$是学习率（learning rate），它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大，在批量梯度下降中，我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jZfagAdY-1575445908529)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575429400255.png)]

在梯度下降算法中，还有一个更微妙的问题，梯度下降中，我们要更新${\theta }_0$和${\theta }_1$ ，当 $j=0$ 和$j=1$时，会产生更新，所以你将更新$J\left({\theta }_0\right)$和$J\left({\theta }_1\right)$。实现梯度下降算法的微妙之处是，在这个表达式中，如果你要更新这个等式，你需要同时更新${\theta }_0$和${\theta }_1$，我的意思是在这个等式中，我们要这样更新：

${\theta }_0$:= ${\theta }_0$ ，并更新${\theta }_1$:= ${\theta }_1$。

实现方法是：你应该计算公式右边的部分，通过那一部分计算出${\theta }_0$和${\theta }_1$的值，然后同时更新${\theta }_0$和${\theta }_1$。

让我进一步阐述这个过程：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-N9QGSCSB-1575445908530)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575429409440.png)]

在梯度下降算法中，这是正确实现同时更新的方法。我不打算解释为什么你需要同时更新，同时更新是梯度下降中的一种常用方法。我们之后会讲到，同步更新是更自然的实现方法。当人们谈到梯度下降时，他们的意思就是同步更新。

在接下来的视频中，我们要进入这个微分项的细节之中。我已经写了出来但没有真正定义，如果你已经修过微积分课程，如果你熟悉偏导数和导数，这其实就是这个微分项：

$\alpha \frac{\partial }{\partial {\theta }_0}J({\theta }_0,{\theta }_1)$，$\alpha \frac{\partial }{\partial {\theta }_1}J({\theta }_0,{\theta }_1)$。

如果你不熟悉微积分，不用担心，即使你之前没有看过微积分，或者没有接触过偏导数，在接下来的视频中，你会得到一切你需要知道，如何计算这个微分项的知识。

梯度下降的直观理解

参考视频: 2 - 6 - Gradient Descent Intuition (12 min).mkv
在之前的视频中，我们给出了一个数学上关于梯度下降的定义，本次视频我们更深入研究一下，更直观地感受一下这个算法是做什么的，以及梯度下降算法的更新过程有什么意义。梯度下降算法如下：

${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J\left(\theta \right)$

描述：对$\theta $赋值，使得$J\left( \theta \right)$按梯度下降最快方向进行，一直迭代下去，最终得到局部最小值。其中$a$是学习率（learning rate），它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-K3Ubrc8x-1575445908531)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575429686477.png)]

对于这个问题，求导的目的，基本上可以说取这个红点的切线，就是这样一条红色的直线，刚好与函数相切于这一点，让我们看看这条红色直线的斜率，就是这条刚好与函数曲线相切的这条直线，这条直线的斜率正好是这个三角形的高度除以这个水平长度，现在，这条线有一个正斜率，也就是说它有正导数，因此，我得到的新的${\theta }_1$，${\theta }_1$更新后等于${\theta }_1$减去一个正数乘以$a$。

这就是我梯度下降法的更新规则：${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J\left(\theta \right)$

让我们来看看如果$a$太小或$a$太大会出现什么情况：

如果$a$太小了，即我的学习速率太小，结果就是只能这样像小宝宝一样一点点地挪动，去努力接近最低点，这样就需要很多步才能到达最低点，所以如果$a$太小的话，可能会很慢，因为它会一点点挪动，它会需要很多步才能到达全局最低点。

如果$a$太大，那么梯度下降法可能会越过最低点，甚至可能无法收敛，下一次迭代又移动了一大步，越过一次，又越过一次，一次次越过最低点，直到你发现实际上离最低点越来越远，所以，如果$a$太大，它会导致无法收敛，甚至发散。

现在，我还有一个问题，当我第一次学习这个地方时，我花了很长一段时间才理解这个问题，如果我们预先把${\theta }_1$放在一个局部的最低点，你认为下一步梯度下降法会怎样工作？

假设你将${\theta }_1$初始化在局部最低点，在这儿，它已经在一个局部的最优处或局部最低点。结果是局部最优点的导数将等于零，因为它是那条切线的斜率。这意味着你已经在局部最优点，它使得${\theta }_1$不再改变，也就是新的${\theta }_1$等于原来的${\theta }_1$，因此，如果你的参数已经处于局部最低点，那么梯度下降法更新其实什么都没做，它不会改变参数的值。这也解释了为什么即使学习速率$a$保持不变时，梯度下降也可以收敛到局部最低点。

我们来看一个例子，这是代价函数$J\left(\theta \right)$。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5YWF6VHR-1575445908531)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575429854299.png)]

我想找到它的最小值，首先初始化我的梯度下降算法，在那个品红色的点初始化，如果我更新一步梯度下降，也许它会带我到这个点，因为这个点的导数是相当陡的。现在，在这个绿色的点，如果我再更新一步，你会发现我的导数，也即斜率，是没那么陡的。随着我接近最低点，我的导数越来越接近零，所以，梯度下降一步后，新的导数会变小一点点。然后我想再梯度下降一步，在这个绿点，我自然会用一个稍微跟刚才在那个品红点时比，再小一点的一步，到了新的红色点，更接近全局最低点了，因此这点的导数会比在绿点时更小。所以，我再进行一步梯度下降时，我的导数项是更小的，${\theta }_1$更新的幅度就会更小。所以随着梯度下降法的运行，你移动的幅度会自动变得越来越小，直到最终移动幅度非常小，你会发现，已经收敛到局部极小值。

回顾一下，在梯度下降法中，当我们接近局部最低点时，梯度下降法会自动采取更小的幅度，这是因为当我们接近局部最低点时，很显然在局部最低时导数等于零，所以当我们接近局部最低时，导数值会自动变得越来越小，所以梯度下降将自动采取较小的幅度，这就是梯度下降的做法。所以实际上没有必要再另外减小$a$。

这就是梯度下降算法，你可以用它来最小化任何代价函数$J$，不只是线性回归中的代价函数$J$。

在接下来的视频中，我们要用代价函数$J$，回到它的本质，线性回归中的代价函数。也就是我们前面得出的平方误差函数，结合梯度下降法，以及平方代价函数，我们会得出第一个机器学习算法，即线性回归算法。

梯度下降的线性回归

参考视频: 2 - 7 - GradientDescentForLinearRegression (6 min).mkv
在以前的视频中我们谈到关于梯度下降算法，梯度下降是很常用的算法，它不仅被用在线性回归上和线性回归模型、平方误差代价函数。在这段视频中，我们要将梯度下降和代价函数结合。我们将用到此算法，并将其应用于具体的拟合直线的线性回归算法里。

梯度下降算法和线性回归算法比较如图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MTU3rNzX-1575445908532)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575430060807.png)]

对我们之前的线性回归问题运用梯度下降法，关键在于求出代价函数的导数，即：
$h_{\theta }\left(x\right)={\theta }_0+{\theta }_{1}x$

$\frac{\partial }{\partial {\theta }_j}J({\theta }_0,{\theta }_1)=\frac{\partial }{\partial {\theta }_j}\frac{1}{2m}{\sum _{i=1}^m\left(h_{\theta }(x^{(i)})-y^{(i)}\right)}^2$

$j=0$ 时：$\frac{\partial }{\partial {\theta }_0}J({\theta }_0,{\theta }_1)=\frac{1}{m}\sum _{i=1}^m\left(h_{\theta }(x^{(i)})-y^{(i)}\right)$

$j=1$ 时：$\frac{\partial }{\partial {\theta }_1}J({\theta }_0,{\theta }_1)=\frac{1}{m}\sum _{i=1}^m\left(\left(h_{\theta }(x^{(i)})-y^{(i)}\right)\cdot x^{(i)}\right)$

则算法改写成：

Repeat {

​ ${\theta }_0:={\theta }_0-a\frac{1}{m}\sum _{i=1}^m\left(h_{\theta }(x^{(i)})-y^{(i)}\right)$

​ ${\theta }_1:={\theta }_1-a\frac{1}{m}\sum _{i=1}^m\left(\left(h_{\theta }(x^{(i)})-y^{(i)}\right)\cdot x^{(i)}\right)$

​ }

我们刚刚使用的算法，有时也称为批量梯度下降。实际上，在机器学习中，通常不太会给算法起名字，但这个名字”批量梯度下降”，指的是在梯度下降的每一步中，我们都用到了所有的训练样本，在梯度下降中，在计算微分求导项时，我们需要进行求和运算，所以，在每一个单独的梯度下降中，我们最终都要计算这样一个东西，这个项需要对所有$m$个训练样本求和。因此，批量梯度下降法这个名字说明了我们需要考虑所有这一"批"训练样本，而事实上，有时也有其他类型的梯度下降法，不是这种"批量"型的，不考虑整个的训练集，而是每次只关注训练集中的一些小的子集。在后面的课程中，我们也将介绍这些方法。

但就目前而言，应用刚刚学到的算法，你应该已经掌握了批量梯度算法，并且能把它应用到线性回归中了，这就是用于线性回归的梯度下降法。

如果你之前学过线性代数，有些同学之前可能已经学过高等线性代数，你应该知道有一种计算代价函数$J$最小值的数值解法，不需要梯度下降这种迭代算法。在后面的课程中，我们也会谈到这个方法，它可以在不需要多步梯度下降的情况下，也能解出代价函数$J$的最小值，这是另一种称为正规方程(normal equations)的方法。实际上在数据量较大的情况下，梯度下降法比正规方程要更适用一些。

现在我们已经掌握了梯度下降，我们可以在不同的环境中使用梯度下降法，我们还将在不同的机器学习问题中大量地使用它。所以，祝贺大家成功学会你的第一个机器学习算法。

在下一段视频中，告诉你泛化的梯度下降算法，这将使梯度下降更加强大。

接下来的内容

参考视频: 2 - 8 - What_'s Next (6 min).mkv
在接下来的一组视频中，我会对线性代数进行一个快速的复习回顾。如果你从来没有接触过向量和矩阵，那么这课件上所有的一切对你来说都是新知识，或者你之前对线性代数有所了解，但由于隔得久了，对其有所遗忘，那就请学习接下来的一组视频，我会快速地回顾你将用到的线性代数知识。

通过它们，你可以实现和使用更强大的线性回归模型。事实上，线性代数不仅仅在线性回归中应用广泛，它其中的矩阵和向量将有助于帮助我们实现之后更多的机器学习模型，并在计算上更有效率。正是因为这些矩阵和向量提供了一种有效的方式来组织大量的数据，特别是当我们处理巨大的训练集时，如果你不熟悉线性代数，如果你觉得线性代数看上去是一个复杂、可怕的概念，特别是对于之前从未接触过它的人，不必担心，事实上，为了实现机器学习算法，我们只需要一些非常非常基础的线性代数知识。通过接下来几个视频，你可以很快地学会所有你需要了解的线性代数知识。具体来说，为了帮助你判断是否有需要学习接下来的一组视频，我会讨论什么是矩阵和向量，谈谈如何加、减 、乘矩阵和向量，讨论逆矩阵和转置矩阵的概念。

如果你十分熟悉这些概念，那么你完全可以跳过这组关于线性代数的选修视频，但是如果你对这些概念仍有些许的不确定，不确定这些数字或这些矩阵的意思，那么请看一看下一组的视频，它会很快地教你一些你需要知道的线性代数的知识，便于之后编写机器学习算法和处理大量数据。

线性代数回顾(Linear Algebra Review)

矩阵和向量

参考视频: 3 - 1 - Matrices and Vectors (9 min).mkv
如图：这个是4×2矩阵，即4行2列，如$m$为行，$n$为列，那么$m\times n$即4×2

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Uf92DeTO-1575445908533)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575430214648.png)]

矩阵的维数即行数×列数

矩阵元素（矩阵项）：$A=\left[\begin{array}{cc}1402& 191\\ 1371& 821\\ 949& 1437\\ 147& 1448\end{array}\right]$

$A_{ij}$指第$i$行，第$j$列的元素。

向量是一种特殊的矩阵，讲义中的向量一般都是列向量，如：
$y=\left[\begin{array}{c}460\\ 232\\ 315\\ 178\end{array}\right]$

为四维列向量（4×1）。

如下图为1索引向量和0索引向量，左图为1索引向量，右图为0索引向量，一般我们用1索引向量。

$y=\left[\begin{array}{c}{y}_1\\ y_2\\ y_3\\ y_4\end{array}\right]$，$y=\left[\begin{array}{c}{y}_0\\ y_1\\ y_2\\ y_3\end{array}\right]$

加法和标量乘法

参考视频: 3 - 2 - Addition and Scalar Multiplication (7 min).mkv
矩阵的加法：行列数相等的可以加。

例：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JIh8XkLc-1575445908533)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575431053908.png)]

矩阵的乘法：每个元素都要乘

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SF1p6dih-1575445908534)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575431095812.png)]

组合算法也类似。

矩阵向量乘法

参考视频: 3 - 3 - Matrix Vector Multiplication (14 min).mkv

矩阵和向量的乘法如图：$m\times n$的矩阵乘以$n\times 1$的向量，得到的是$m\times 1$的向量

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-eBl3idzV-1575445908534)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575431123683.png)]

算法举例：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TM8G5OiD-1575445908535)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575431133404.png)]

矩阵乘法

参考视频: 3 - 4 - Matrix Matrix Multiplication (11 min).mkv
矩阵乘法：

$m\times n$矩阵乘以$n\times o$矩阵，变成$m\times o$矩阵。

如果这样说不好理解的话就举一个例子来说明一下，比如说现在有两个矩阵$A$和$B$，那么它们的乘积就可以表示为图中所示的形式。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TF5RWmcY-1575445908536)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575431168523.png)]

矩阵乘法的性质

参考视频: 3 - 5 - Matrix Multiplication Properties (9 min).mkv
矩阵乘法的性质：

矩阵的乘法不满足交换律：$A\times B\ne B\times A$

矩阵的乘法满足结合律。即：$A\times (B\times C)=(A\times B)\times C$

单位矩阵：在矩阵的乘法中，有一种矩阵起着特殊的作用，如同数的乘法中的1,我们称这种矩阵为单位矩阵．它是个方阵，一般用 $I$ 或者 $E$ 表示，本讲义都用 $I$ 代表单位矩阵，从左上角到右下角的对角线（称为主对角线）上的元素均为1以外全都为0。如：

$A{A}^{-1}=A^{-1}A=I$

对于单位矩阵，有$AI=IA=A$

逆、转置

参考视频: 3 - 6 - Inverse and Transpose (11 min).mkv
矩阵的逆：如矩阵$A$是一个$m\times m$矩阵（方阵），如果有逆矩阵，则：$A{A}^{-1}=A^{-1}A=I$

我们一般在OCTAVE或者MATLAB中进行计算矩阵的逆矩阵。

矩阵的转置：设$A$为$m\times n$阶矩阵（即$m$行$n$列），第$i $行$j $列的元素是$a(i,j)$，即：$A=a(i,j)$

定义$A$的转置为这样一个$n\times m$阶矩阵$B$，满足$B=a(j,i)$，即 $b(i,j)=a(j,i)$（$B$的第$i$行第$j$列元素是$A$的第$j$行第$i$列元素），记$A^T=B$。(有些书记为A’=B）

直观来看，将$A$的所有元素绕着一条从第1行第1列元素出发的右下方45度的射线作镜面反转，即得到$A$的转置。

例：

${\left|\begin{array}{cc}a& b\\ c& d\\ e& f\end{array}\right|}^T=\left|\begin{array}{ccc}a& c& e\\ b& d& f\end{array}\right|$

矩阵的转置基本性质:

$ {{\left( A\pm B \right)}^{T}}={{A}{T}}\pm {{B}^{T}} $
${\left(A\times B\right)}^T=B^T\times A^T$
${{\left( {{A}^{T}} \right)}^{T}}=A $
${{\left( KA \right)}^{T}}=K{{A}{T}} $

matlab中矩阵转置：直接打一撇，x=y'。

多变量线性回归(Linear Regression with Multiple Variables)

多维特征

参考视频: 4 - 1 - Multiple Features (8 min).mkv
目前为止，我们探讨了单变量/特征的回归模型，现在我们对房价模型增加更多的特征，例如房间数楼层等，构成一个含有多个变量的模型，模型中的特征为$\left(x_1,x_2,...,x_n\right)$。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1SSXriYz-1575445908536)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575431645491.png)]

增添更多特征后，我们引入一系列新的注释：

$n$ 代表特征的数量

$x^{\left(i\right)}$代表第 $i$ 个训练实例，是特征矩阵中的第$i$行，是一个向量（vector）。

比方说，上图的

$x^{(2)}\text{=}\left[\begin{array}{c}1416\\ 3\\ 2\\ 40\end{array}\right]$，

$x_j^{\left(i\right)}$代表特征矩阵中第 $i$ 行的第 $j$ 个特征，也就是第 $i$ 个训练实例的第 $j$ 个特征。

如上图的$x_2^{\left(2\right)}=3,x_3^{\left(2\right)}=2$，

支持多变量的假设 $h$ 表示为：$h_{\theta }\left(x\right)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+...+{\theta }_n{x}_n$，

这个公式中有$n+1$个参数和$n$个变量，为了使得公式能够简化一些，引入$x_0=1$，则公式转化为：$h_{\theta }\left(x\right)={\theta }_0{x}_0+{\theta }_1{x}_1+{\theta }_2{x}_2+...+{\theta }_n{x}_n$

此时模型中的参数是一个$n+1$维的向量，任何一个训练实例也都是$n+1$维的向量，特征矩阵$X$的维度是 $m\ast (n+1)$。 因此公式可以简化为：$h_{\theta }\left(x\right)={\theta }^{T}X$，其中上标$T$代表矩阵转置。

多变量梯度下降

参考视频: 4 - 2 - Gradient Descent for Multiple Variables (5 min).mkv
与单变量线性回归类似，在多变量线性回归中，我们也构建一个代价函数，则这个代价函数是所有建模误差的平方和，即：$J\left({\theta }_0,{\theta }_1...{\theta }_n\right)=\frac{1}{2m}\sum _{i=1}^m{\left(h_{\theta }\left(x^{\left(i\right)}\right)-y^{\left(i\right)}\right)}^2$ ，

其中：$h_{\theta }\left(x\right)={\theta }^{T}X={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+...+{\theta }_n{x}_n$ ，

我们的目标和单变量线性回归问题中一样，是要找出使得代价函数最小的一系列参数。
多变量线性回归的批量梯度下降算法为：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rDxDUDuW-1575445908537)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575431758447.png)]

即：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LHIrtm0Y-1575445908537)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575431766568.png)]

求导数后得到：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7wTPxTFs-1575445908538)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575431781513.png)]

当$n>=1$时，
${\theta }_0:={\theta }_0-a\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_0^{(i)}$

${\theta }_1:={\theta }_1-a\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_1^{(i)}$

${\theta }_2:={\theta }_2-a\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_2^{(i)}$

我们开始随机选择一系列的参数值，计算所有的预测结果后，再给所有的参数一个新的值，如此循环直到收敛。

代码示例：

计算代价函数
$J\left(\theta \right)=\frac{1}{2m}\sum _{i=1}^m{\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)}^2$
其中：$h_{\theta }\left(x\right)={\theta }^{T}X={\theta }_0{x}_0+{\theta }_1{x}_1+{\theta }_2{x}_2+...+{\theta }_n{x}_n$

Python 代码：

def computeCost(X, y, theta):
    inner = np.power(((X * theta.T) - y), 2)
    return np.sum(inner) / (2 * len(X))

梯度下降法实践1-特征缩放

参考视频: 4 - 3 - Gradient Descent in Practice I - Feature Scaling (9 min).mkv

在我们面对多维特征问题的时候，我们要保证这些特征都具有相近的尺度，这将帮助梯度下降算法更快地收敛。

以房价问题为例，假设我们使用两个特征，房屋的尺寸和房间的数量，尺寸的值为 0-2000平方英尺，而房间数量的值则是0-5，以两个参数分别为横纵坐标，绘制代价函数的等高线图能，看出图像会显得很扁，梯度下降算法需要非常多次的迭代才能收敛。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-f8kgZv1w-1575445908538)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575431844502.png)]

解决的方法是尝试将所有特征的尺度都尽量缩放到-1到1之间。如图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4CBHnOb2-1575445908539)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575431851977.png)]

最简单的方法是令：$x_n=\frac{x_n-{\mu }_n}{s_n}$，其中 ${\mu }_n$是平均值，$s_n$是标准差。

梯度下降法实践2-学习率

参考视频: 4 - 4 - Gradient Descent in Practice II - Learning Rate (9 min).mkv
梯度下降算法收敛所需要的迭代次数根据模型的不同而不同，我们不能提前预知，我们可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oxkpoTmg-1575445908540)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575431866164.png)]

也有一些自动测试是否收敛的方法，例如将代价函数的变化值与某个阀值（例如0.001）进行比较，但通常看上面这样的图表更好。

梯度下降算法的每次迭代受到学习率的影响，如果学习率$a$过小，则达到收敛所需的迭代次数会非常高；如果学习率$a$过大，每次迭代可能不会减小代价函数，可能会越过局部最小值导致无法收敛。

通常可以考虑尝试些学习率：

$\alpha =0.01，0.03，0.1，0.3，1，3，10$

特征和多项式回归

参考视频: 4 - 5 - Features and Polynomial Regression (8 min).mkv

如房价预测问题，

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Rl52jLVx-1575445908541)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575431954385.png)]

$h_{\theta }\left(x\right)={\theta }_0+{\theta }_1\times frontage+{\theta }_2\times depth$

$x_1=frontage$（临街宽度），$x_2=depth$（纵向深度），$x=frontage\ast depth=area$（面积），则：$h_{\theta }\left(x\right)={\theta }_0+{\theta }_{1}x$。
线性回归并不适用于所有数据，有时我们需要曲线来适应我们的数据，比如一个二次方模型：$h_{\theta }\left(x\right)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2^2$
或者三次方模型： $h_{\theta }\left(x\right)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2^2+{\theta }_3{x}_3^3$

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-l5Xd5VRd-1575445908541)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575432002700.png)]

通常我们需要先观察数据然后再决定准备尝试怎样的模型。 另外，我们可以令：

$x_2=x_2^2,x_3=x_3^3$，从而将模型转化为线性回归模型。

根据函数图形特性，我们还可以使：

$h_{\theta }(x)={\theta }_0\text{+}{\theta }_1(size)+{\theta }_2{(size)}^2$

或者:

$h_{\theta }(x)={\theta }_0\text{+}{\theta }_1(size)+{\theta }_2\sqrt{size}$

注：如果我们采用多项式回归模型，在运行梯度下降算法前，特征缩放非常有必要。

正规方程

参考视频: 4 - 6 - Normal Equation (16 min).mkv
到目前为止，我们都在使用梯度下降算法，但是对于某些线性回归问题，正规方程方法是更好的解决方案。如：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OoN6OXrc-1575445908542)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575432364923.png)]

正规方程是通过求解下面的方程来找出使得代价函数最小的参数的：$\frac{\partial }{\partial {\theta }_j}J\left({\theta }_j\right)=0$ 。
假设我们的训练集特征矩阵为 $X$（包含了 $x_0=1$）并且我们的训练集结果为向量 $y$，则利用正规方程解出向量 $\theta ={\left(X^{T}X\right)}^{-1}{X}^{T}y$ 。
上标 T 代表矩阵转置，上标-1 代表矩阵的逆。设矩阵$A=X^{T}X$，则：${\left(X^{T}X\right)}^{-1}=A^{-1}$
以下表示数据为例：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dJ1m7jpA-1575445908543)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575432408169.png)]

即：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-c45uPaOP-1575445908543)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575432413948.png)]

运用正规方程方法求解参数：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gzayCvwE-1575445908544)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575432420036.png)]

在 Octave 中，正规方程写作：

pinv(X'*X)*X'*y

注：对于那些不可逆的矩阵（通常是因为特征之间不独立，如同时包含英尺为单位的尺寸和米为单位的尺寸两个特征，也有可能是特征数量大于训练集的数量），正规方程方法是不能用的。

梯度下降与正规方程的比较：

梯度下降	正规方程
需要选择学习率$\alpha$	不需要
需要多次迭代	一次运算得出
当特征数量$n$大时也能较好适用	需要计算${\left(X^{T}X\right)}^{-1}$ 如果特征数量n较大则运算代价大，因为矩阵逆的计算时间复杂度为$O\left(n^3\right)$，通常来说当$n$小于10000 时还是可以接受的
适用于各种类型的模型	只适用于线性模型，不适合逻辑回归模型等其他模型

总结一下，只要特征变量的数目并不大，标准方程是一个很好的计算参数$\theta $的替代方法。具体地说，只要特征变量数量小于一万，我通常使用标准方程法，而不使用梯度下降法。

随着我们要讲的学习算法越来越复杂，例如，当我们讲到分类算法，像逻辑回归算法，我们会看到，实际上对于那些算法，并不能使用标准方程法。对于那些更复杂的学习算法，我们将不得不仍然使用梯度下降法。因此，梯度下降法是一个非常有用的算法，可以用在有大量特征变量的线性回归问题。或者我们以后在课程中，会讲到的一些其他的算法，因为标准方程法不适合或者不能用在它们上。但对于这个特定的线性回归模型，标准方程法是一个比梯度下降法更快的替代算法。所以，根据具体的问题，以及你的特征变量的数量，这两种算法都是值得学习的。

正规方程的python实现：

import numpy as np
    
 def normalEqn(X, y):
    
   theta = np.linalg.inv(X.T@X)@X.T@y #X.T@X等价于X.T.dot(X)
    
   return theta

正规方程及不可逆性（可选）

参考视频: 4 - 7 - Normal Equation Noninvertibility (Optional) (6 min).mkv
在这段视频中谈谈正规方程 ( normal equation )，以及它们的不可逆性。
由于这是一种较为深入的概念，并且总有人问我有关这方面的问题，因此，我想在这里来讨论它，由于概念较为深入，所以对这段可选材料大家放轻松吧，也许你可能会深入地探索下去，并且会觉得理解以后会非常有用。但即使你没有理解正规方程和线性回归的关系，也没有关系。

我们要讲的问题如下：$\theta ={\left(X^{T}X\right)}^{-1}{X}^{T}y$

备注：本节最后我把推导过程写下。

有些同学曾经问过我，当计算 $\theta$=inv(X'X ) X'y ，那对于矩阵$X^{\prime }X$的结果是不可逆的情况咋办呢?
如果你懂一点线性代数的知识，你或许会知道，有些矩阵可逆，而有些矩阵不可逆。我们称那些不可逆矩阵为奇异或退化矩阵。
问题的重点在于$X^{\prime }X$的不可逆的问题很少发生，在Octave里，如果你用它来实现$\theta$的计算，你将会得到一个正常的解。在Octave里，有两个函数可以求解矩阵的逆，一个被称为pinv()，另一个是inv()，这两者之间的差异是些许计算过程上的，一个是所谓的伪逆，另一个被称为逆。使用pinv() 函数可以展现数学上的过程，这将计算出$\theta$的值，即便矩阵$X^{\prime }X$是不可逆的。

在pinv() 和 inv() 之间，又有哪些具体区别呢 ?

其中inv() 引入了先进的数值计算的概念。例如，在预测住房价格时，如果$x_1$是以英尺为尺寸规格计算的房子，$x_2$是以平方米为尺寸规格计算的房子，同时，你也知道1米等于3.28英尺 ( 四舍五入到两位小数 )，这样，你的这两个特征值将始终满足约束：$x_1=x_2\ast {\left(3.28\right)}^2$。
实际上，你可以用这样的一个线性方程，来展示那两个相关联的特征值，矩阵$X^{\prime }X$将是不可逆的。

第二个原因是，在你想用大量的特征值，尝试实践你的学习算法的时候，可能会导致矩阵$X^{\prime }X$的结果是不可逆的。
具体地说，在$m$小于或等于n的时候，例如，有$m$等于10个的训练样本也有$n$等于100的特征数量。要找到适合的$(n+1)$ 维参数矢量$\theta$，这将会变成一个101维的矢量，尝试从10个训练样本中找到满足101个参数的值，这工作可能会让你花上一阵子时间，但这并不总是一个好主意。因为，正如我们所看到你只有10个样本，以适应这100或101个参数，数据还是有些少。

稍后我们将看到，如何使用小数据样本以得到这100或101个参数，通常，我们会使用一种叫做正则化的线性代数方法，通过删除某些特征或者是使用某些技术，来解决当$m$比$n$小的时候的问题。即使你有一个相对较小的训练集，也可使用很多的特征来找到很多合适的参数。
总之当你发现的矩阵$X^{\prime }X$的结果是奇异矩阵，或者找到的其它矩阵是不可逆的，我会建议你这么做。

首先，看特征值里是否有一些多余的特征，像这些$x_1$和$x_2$是线性相关的，互为线性函数。同时，当有一些多余的特征时，可以删除这两个重复特征里的其中一个，无须两个特征同时保留，将解决不可逆性的问题。因此，首先应该通过观察所有特征检查是否有多余的特征，如果有多余的就删除掉，直到他们不再是多余的为止，如果特征数量实在太多，我会删除些 用较少的特征来反映尽可能多内容，否则我会考虑使用正规化方法。
如果矩阵$X^{\prime }X$是不可逆的，（通常来说，不会出现这种情况），如果在Octave里，可以用伪逆函数pinv() 来实现。这种使用不同的线性代数库的方法被称为伪逆。即使$X^{\prime }X$的结果是不可逆的，但算法执行的流程是正确的。总之，出现不可逆矩阵的情况极少发生，所以在大多数实现线性回归中，出现不可逆的问题不应该过多的关注$X^{T}X$是不可逆的。

增加内容：

$\theta ={\left(X^{T}X\right)}^{-1}{X}^{T}y$ 的推导过程：

$J\left(\theta \right)=\frac{1}{2m}\sum _{i=1}^m{\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)}^2$
其中：$h_{\theta }\left(x\right)={\theta }^{T}X={\theta }_0{x}_0+{\theta }_1{x}_1+{\theta }_2{x}_2+...+{\theta }_n{x}_n$

将向量表达形式转为矩阵表达形式，则有$J(\theta )=\frac{1}{2}{\left(X\theta -y\right)}^2$ ，其中$X$为$m$行$n$列的矩阵（$m$为样本个数，$n$为特征个数），$\theta$为$n$行1列的矩阵，$y$为$m$行1列的矩阵，对$J(\theta )$进行如下变换

$J(\theta )=\frac{1}{2}{\left(X\theta -y\right)}^T\left(X\theta -y\right)$

​ $=\frac{1}{2}\left({\theta }^T{X}^T-y^T\right)\left(X\theta -y\right)$

​ $=\frac{1}{2}\left({\theta }^T{X}^{T}X\theta -{\theta }^T{X}^{T}y-y^{T}X\theta -y^{T}y\right)$

接下来对$J(\theta )$偏导，需要用到以下几个矩阵的求导法则:

$\frac{dAB}{dB}=A^T$

$\frac{d{X}^{T}AX}{dX}=2AX$

所以有:

$\frac{\partial J\left(\theta \right)}{\partial \theta }=\frac{1}{2}\left(2X^{T}X\theta -X^{T}y-(y^{T}X{)}^T-0\right)$

$=\frac{1}{2}\left(2X^{T}X\theta -X^{T}y-X^{T}y-0\right)$

​ $=X^{T}X\theta -X^{T}y$

令$\frac{\partial J\left(\theta \right)}{\partial \theta }=0$,

则有$\theta ={\left(X^{T}X\right)}^{-1}{X}^{T}y$

Octave教程(Octave Tutorial)

基本操作

参考视频: 5 - 1 - Basic Operations (14 min).mkv

在这段视频中，我将教你一种编程语言：Octave语言。你能够用它来非常迅速地实现这门课中我们已经学过的，或者将要学的机器学习算法。

过去我一直尝试用不同的编程语言来教授机器学习，包括C++、Java、Python、Numpy和Octave。我发现当使用像Octave这样的高级语言时，学生能够更快更好地学习并掌握这些算法。事实上，在硅谷，我经常看到进行大规模的机器学习项目的人，通常使用的程序语言就是Octave。(编者注：这是当时的情况，现在主要是用Python)

Octave是一种很好的原始语言(prototyping language)，使用Octave你能快速地实现你的算法，剩下的事情，你只需要进行大规模的资源配置，你只用再花时间用C++或Java这些语言把算法重新实现就行了。开发项目的时间是很宝贵的，机器学习的时间也是很宝贵的。所以，如果你能让你的学习算法在Octave上快速的实现，基本的想法实现以后，再用C++或者Java去改写，这样你就能节省出大量的时间。

据我所见，人们使用最多的用于机器学习的原始语言是Octave、MATLAB、Python、NumPy 和R。

Octave很好，因为它是开源的。当然MATLAB也很好，但它不是每个人都买得起的。(貌似国内学生喜欢用收费的matlab，matlab功能要比Octave强大的多，网上有各种D版可以下载)。这次机器学习课的作业也是用matlab的。如果你能够使用matlab，你也可以在这门课里面使用。

如果你会Python、NumPy或者R语言，我也见过有人用 R的，据我所知，这些人不得不中途放弃了，因为这些语言在开发上比较慢，而且，因为这些语言如：Python、NumPy的语法相较于Octave来说，还是更麻烦一点。正因为这样，所以我强烈建议不要用NumPy或者R来完整这门课的作业，我建议在这门课中用Octave来写程序。

本视频将快速地介绍一系列的命令，目标是迅速地展示，通过这一系列Octave的命令，让你知道Octave能用来做什么。

启动Octave：

现在打开Octave，这是Octave命令行。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LeuL0e7Y-1575445908544)(https://www.github.com/OneJane/blog/raw/master/小书匠/e2c2dcc31f19ac255566fa616799d496.png)]

现在让我示范最基本的Octave代码：

输入5 + 6，然后得到11。

输入3 – 2、5×8、1/2、2^6等等，得到相应答案。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GJbcqxzi-1575445908545)(https://www.github.com/OneJane/blog/raw/master/小书匠/6dcdf4a7c0d56787648d4a1902034150.png)]

这些都是基本的数学运算。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uVJvLyhj-1575445908545)(https://www.github.com/OneJane/blog/raw/master/小书匠/f8507899953ed2de68e6b2b83554f9ea.png)]
你也可以做逻辑运算，例如 12，计算结果为 false (假)，这里的百分号命令表示注释，12 计算结果为假，这里用0表示。

请注意，不等于符号的写法是这个波浪线加上等于符号 ( ~= )，而不是等于感叹号加等号( != )，这是和其他一些编程语言中不太一样的地方。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uI4DX7Kr-1575445908546)(https://www.github.com/OneJane/blog/raw/master/小书匠/126b2a5c4b5bfb24e5c21cd080159530.png)]
让我们看看逻辑运算 1 && 0，使用双&符号表示逻辑与，1 && 0判断为假，1和0的或运算 1 || 0，其计算结果为真。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gg8WtFhO-1575445908546)(https://www.github.com/OneJane/blog/raw/master/小书匠/fec0936e2a78c0fe8c9e3ed107614a31.png)]
还有异或运算 如XOR ( 1, 0 )，其返回值为1

从左向右写着 Octave 324.x版本，是默认的Octave提示，它显示了当前Octave的版本，以及相关的其它信息。

如果你不想看到那个提示，这里有一个隐藏的命令：

输入命令

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ObPjSSck-1575445908547)(https://www.github.com/OneJane/blog/raw/master/小书匠/8d63fe546c12a7e9eb658118d76288f7.png)]
现在命令提示已经变得简化了。

接下来，我们将谈到Octave的变量。

现在写一个变量，对变量$A$赋值为3，并按下回车键，显示变量$A$等于3。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mOVRivn7-1575445908547)(https://www.github.com/OneJane/blog/raw/master/小书匠/a537df35ccc9ff83a3c7518362e2f729.png)]
如果你想分配一个变量，但不希望在屏幕上显示结果，你可以在命令后加一个分号，可以抑制打印输出，敲入回车后，不打印任何东西。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1c3g5hbv-1575445908548)(https://www.github.com/OneJane/blog/raw/master/小书匠/c11786828c587189891a9ef02f041ab7.png)]
其中这句命令不打印任何东西。

现在举一个字符串的例子：变量$b$等于"hi"。

$c$等于3大于等于1，所以，现在$c$变量的值是真。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-y9Gm0FPV-1575445908549)(https://www.github.com/OneJane/blog/raw/master/小书匠/acedf91b6b39d551e62a89f2e0955628.png)]
如果你想打印出变量，或显示一个变量，你可以像下面这么做：

设置$a$等于圆周率$\pi$，如果我要打印该值，那么只需键入a像这样 就打印出来了。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ClFjhyUs-1575445908549)(https://www.github.com/OneJane/blog/raw/master/小书匠/2cdc09b8bf67e546df7284ba74601c66.png)]
对于更复杂的屏幕输出，也可以用DISP命令显示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-U68SHIB1-1575445908550)(https://www.github.com/OneJane/blog/raw/master/小书匠/dfcd1d37526824726d85a655f8951249.png)]
这是一种，旧风格的C语言语法，对于之前就学过C语言的同学来说，你可以使用这种基本的语法来将结果打印到屏幕。

例如 ^{T}命令的六个小数：0.6%f ,a，这应该打印$\pi$的6位小数形式。

也有一些控制输出长短格式的快捷命令：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gdi2HVMJ-1575445908551)(https://www.github.com/OneJane/blog/raw/master/小书匠/ba8f0c3d2d8f017e0f7a611aa5be75d6.png)]
下面，让我们来看看向量和矩阵：

比方说 建立一个矩阵$A$：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TMKKwxVe-1575445908551)(https://www.github.com/OneJane/blog/raw/master/小书匠/693ebb444501838dd9b69520fff54be0.png)]
对$A$矩阵进行赋值，考虑到这是一个三行两列的矩阵，你同样可以用向量。

建立向量$V$并赋值1 2 3，$V$是一个行向量，或者说是一个3 ( 列 )×1 ( 行 )的向量，或者说，一行三列的矩阵。

如果我想，分配一个列向量，我可以写“1;2;3”，现在便有了一个3 行 1 列的向量，同时这是一个列向量。

下面是一些更为有用的符号，如：

V=1：0.1：2

这个该如何理解呢：这个集合$v$是一组值，从数值1开始，增量或说是步长为0.1，直到增加到2，按照这样的方法对向量$V$操作，可以得到一个行向量，这是一个1行11列的矩阵，其矩阵的元素是1
1.1 1.2 1.3，依此类推，直到数值2。

我也可以建立一个集合$v$并用命令“1:6”进行赋值，这样$V$就被赋值了1至6的六个整数。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8Q5CJyzp-1575445908552)(https://www.github.com/OneJane/blog/raw/master/小书匠/1cdbd87db83a4184098cd6d5ee3c6a87.png)]
这里还有一些其他的方法来生成矩阵

例如“ones(2, 3)”，也可以用来生成矩阵：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EwjEZmEi-1575445908552)(https://www.github.com/OneJane/blog/raw/master/小书匠/5d2b25d4078a276091b9c00812674fa9.png)]
元素都为2，两行三列的矩阵，就可以使用这个命令：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YwCsPz8p-1575445908553)(https://www.github.com/OneJane/blog/raw/master/小书匠/21985f8690965598d4a17e3a6e7fee94.png)]
你可以把这个方法当成一个生成矩阵的快速方法。

$w$为一个一行三列的零矩阵，一行三列的$A$矩阵里的元素全部是零：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NkLh97WG-1575445908553)(https://www.github.com/OneJane/blog/raw/master/小书匠/846b48ec79c9fcee05b20767dcc89558.png)]
还有很多的方式来生成矩阵。

如果我对$W$进行赋值，用Rand命令建立一个一行三列的矩阵，因为使用了Rand命令，则其一行三列的元素均为随机值，如“rand(3,3)”命令，这就生成了一个3×3的矩阵，并且其所有元素均为随机。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Dhz1fn3T-1575445908553)(https://www.github.com/OneJane/blog/raw/master/小书匠/0de6e7054e869a82060cefa9968cd56b.png)]
数值介于0和1之间，所以，正是因为这一点，我们可以得到数值均匀介于0和1之间的元素。

如果，你知道什么是高斯随机变量，或者，你知道什么是正态分布的随机变量，你可以设置集合$W$，使其等于一个一行三列的$N$矩阵，并且，来自三个值，一个平均值为0的高斯分布，方差或者等于1的标准偏差。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-B2vNn1OF-1575445908554)(https://www.github.com/OneJane/blog/raw/master/小书匠/048f3cac1c32e3dc56160849c4dd60b0.png)]
还可以设置地更复杂：

并用hist命令绘制直方图。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-w49aBQUW-1575445908555)(https://www.github.com/OneJane/blog/raw/master/小书匠/10c06cc39058da2c5eef696d75e65a2c.png)]
绘制单位矩阵：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AABFaepn-1575445908555)(https://www.github.com/OneJane/blog/raw/master/小书匠/08d11f870c5b30536f1965507fa7e7dc.png)]
如果对命令不清楚，建议用help命令：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6OBRhXXe-1575445908556)(https://www.github.com/OneJane/blog/raw/master/小书匠/79b55d71cf434126f3d8457a3a615d18.png)]
以上讲解的内容都是Octave的基本操作。希望你能通过上面的讲解，自己练习一些矩阵、乘、加等操作，将这些操作在Octave中熟练运用。

在接下来的视频中，将会涉及更多复杂的命令，并使用它们在Octave中对数据进行更多的操作。

移动数据

参考视频: 5 - 2 - Moving Data Around (16 min).mkv

在这段关于 Octave的辅导课视频中，我将开始介绍如何在 Octave 中移动数据。

如果你有一个机器学习问题，你怎样把数据加载到 Octave 中？

怎样把数据存入一个矩阵？

如何对矩阵进行相乘？

如何保存计算结果？

如何移动这些数据并用数据进行操作？

进入我的 Octave 窗口，

我键入$A$，得到我们之前构建的矩阵 $A$，也就是用这个命令生成的：

A = [1 2; 3 4; 5 6]

这是一个3行2列的矩阵，Octave 中的 size() 命令返回矩阵的尺寸。

所以 size(A) 命令返回3 2

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-l3OZovcM-1575445908556)(https://markdown.xiaoshujiang.com/img/spinner.gif “[[[1575432885877]]]” )]
实际上，size() 命令返回的是一个 1×2 的矩阵，我们可以用 $sz$ 来存放。

设置 sz = size(A)

因此 $sz$ 就是一个1×2的矩阵，第一个元素是3，第二个元素是2。

所以如果键入 size(sz) 看看 $sz$ 的尺寸，返回的是1 2，表示是一个1×2的矩阵，1 和 2分别表示矩阵$sz$的维度 。

你也可以键入 size(A, 1)，将返回3，这个命令会返回$A$矩阵的第一个元素，$A$矩阵的第一个维度的尺寸，也就是 $A$ 矩阵的行数。

同样，命令 size(A, 2)，将返回2，也就是 $A$ 矩阵的列数。

如果你有一个向量 $v$，假如 v = [1 2 3 4]，然后键入length(v)，这个命令将返回最大维度的大小，返回4。

你也可以键入length(A)，由于矩阵$A$是一个3×2的矩阵，因此最大的维度应该是3，因此该命令会返回3。

但通常我们还是对向量使用 $length$ 命令，而不是对矩阵使用 length 命令，比如
length([1;2;3;4;5])，返回5。

如何在系统中加载数据和寻找数据：

当我们打开 Octave 时，我们通常已经在一个默认路径中，这个路径是 Octave的安装位置，pwd 命令可以显示出Octave 当前所处路径。

cd命令，意思是改变路径，我可以把路径改为C:\Users\ang\Desktop，这样当前目录就变为了桌面。

如果键入 ls，ls 来自于一个 Unix 或者 Linux 命令，ls命令将列出我桌面上的所有路径。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-a38cdbJ0-1575445908557)(https://www.github.com/OneJane/blog/raw/master/小书匠/0de527966203108b7efa1b6730bd966c.png)]
事实上，我的桌面上有两个文件：featuresX.dat 和priceY.dat，是两个我想解决的机器学习问题。

featuresX文件如这个窗口所示，是一个含有两列数据的文件，其实就是我的房屋价格数据，数据集中有47行，第一个房子样本，面积是2104平方英尺，有3个卧室，第二套房子面积为1600，有3个卧室等等。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EoJZPMUu-1575445908558)(https://www.github.com/OneJane/blog/raw/master/小书匠/e4080d69119a0e408581c81a66e133c8.png)]
priceY这个文件就是训练集中的价格数据，所以 featuresX 和priceY就是两个存放数据的文档，那么应该怎样把数据读入 Octave 呢？我们只需要键入featuresX.dat，这样我将加载了 featuresX 文件。同样地我可以加载priceY.dat。其实有好多种办法可以完成，如果你把命令写成字符串的形式load('featureX.dat')，也是可以的，这跟刚才的命令效果是相同的，只不过是把文件名写成了一个字符串的形式，现在文件名被存在一个字符串中。Octave中使用引号来表示字符串。

另外 who 命令，能显示出 在我的 Octave工作空间中的所有变量

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hH7sRKke-1575445908558)(https://www.github.com/OneJane/blog/raw/master/小书匠/7e85f313f721f53f3ae74664210a7a25.png)]
所以我可以键入featuresX 回车，来显示 featuresX

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ADMUuXWr-1575445908559)(https://www.github.com/OneJane/blog/raw/master/小书匠/e49f56ceddd34dce986ae1dbdc399762.png)]
这些就是存在里面的数据。

还可以键入 size(featuresX)，得出的结果是 47 2，代表这是一个47×2的矩阵。

类似地，输入 size(priceY)，结果是 47
1，表示这是一个47维的向量，是一个列矩阵，存放的是训练集中的所有价格$Y$ 的值。

who 函数能让你看到当前工作空间中的所有变量，同样还有另一个 whos命令，能更详细地进行查看。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kasD4Hod-1575445908559)(https://www.github.com/OneJane/blog/raw/master/小书匠/e8207c74976c4443d1ea25ec2a3b8477.png)]
同样也列出我所有的变量，不仅如此，还列出了变量的维度。

double 意思是双精度浮点型，这也就是说，这些数都是实数，是浮点数。

如果你想删除某个变量，你可以使用 clear 命令，我们键入 clear featuresX，然后再输入 whos 命令，你会发现 featuresX 消失了。

另外，我们怎么储存数据呢？

我们设变量 V= priceY(1:10)

这表示的是将向量 $Y $的前10个元素存入 $V$中。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-L6WJCSKL-1575445908560)(https://www.github.com/OneJane/blog/raw/master/小书匠/a8c3b363f13820b4fc6463c7520ab58c.png)]
假如我们想把它存入硬盘，那么用 save hello.mat v 命令，这个命令会将变量$V$存成一个叫 hello.mat 的文件，让我们回车，现在我的桌面上就出现了一个新文件，名为hello.mat。

由于我的电脑里同时安装了 MATLAB，所以这个图标上面有 MATLAB的标识，因为操作系统把文件识别为 MATLAB文件。如果在你的电脑上图标显示的不一样的话，也没有关系。

现在我们清除所有变量，直接键入clear，这样将删除工作空间中的所有变量，所以现在工作空间中啥都没了。

但如果我载入 hello.mat 文件，我又重新读取了变量 $v$，因为我之前把变量$v$存入了hello.mat 文件中，所以我们刚才用 save命令做了什么。这个命令把数据按照二进制形式储存，或者说是更压缩的二进制形式，因此，如果$v$是很大的数据，那么压缩幅度也更大，占用空间也更小。如果你想把数据存成一个人能看懂的形式，那么可以键入：

save hello.txt v -ascii

这样就会把数据存成一个文本文档，或者将数据的 ascii 码存成文本文档。

我键入了这个命令以后，我的桌面上就有了 hello.txt文件。如果打开它，我们可以发现这个文本文档存放着我们的数据。

这就是读取和储存数据的方法。

接下来我们再来讲讲操作数据的方法：

假如 $A$ 还是那个矩阵

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Iawb2cIV-1575445908560)(https://www.github.com/OneJane/blog/raw/master/小书匠/b39bf4e9212442464fe2f568dbe4fa0c.png)]
跟刚才一样还是那个 3×2 的矩阵，现在我们加上索引值，比如键入 A(3,2)

这将索引到$A$ 矩阵的 (3,2) 元素。这就是我们通常书写矩阵的形式，写成 $A$ 32，3和2分别表示矩阵的第三行和第二列对应的元素，因此也就对应 6。

我也可以键入A(2,:) 来返回第二行的所有元素，冒号表示该行或该列的所有元素。

类似地，如果我键入 A(:,2)，这将返回 $A$ 矩阵第二列的所有元素，这将得到 2 4 6。

这表示返回$A$ 矩阵的第二列的所有元素。

你也可以在运算中使用这些较为复杂的索引。

我再给你展示几个例子，可能你也不会经常使用，但我还是输入给你看 A([1 3],:)，这个命令意思是取 $A$ 矩阵第一个索引值为1或3的元素，也就是说我取的是A矩阵的第一行和第三行的每一列，冒号表示的是取这两行的每一列元素，即：

可能这些比较复杂一点的索引操作你会经常用到。

我们还能做什么呢？依然是 $A$ 矩阵，A(:,2) 命令返回第二列。

你也可以为它赋值，我可以取 $A$ 矩阵的第二列，然后将它赋值为10 11 12，我实际上是取出了 $A$ 的第二列，然后把一个列向量[10;11;12]赋给了它，因此现在 $A$ 矩阵的第一列还是 1 3 5，第二列就被替换为 10 11 12。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TfXhqxov-1575445908561)(https://www.github.com/OneJane/blog/raw/master/小书匠/f47bda45fd9beef6c600ebd48d163617.png)]
接下来一个操作，让我们把 $A $设为A = [A, [100, 101,102]]，这样做的结果是在原矩阵的右边附加了一个新的列矩阵，就是把 $A$矩阵设置为原来的 $A$ 矩阵再在右边附上一个新添加的列矩阵。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-CKSwOQaP-1575445908562)(https://www.github.com/OneJane/blog/raw/master/小书匠/2e1c68a99a23d993674f08151e77dd44.png)]
最后，还有一个小技巧，如果你就输入 A(:)，这是一个很特别的语法结构，意思是把 $A$中的所有元素放入一个单独的列向量，这样我们就得到了一个 9×1 的向量，这些元素都是$A$ 中的元素排列起来的。

再来几个例子：

我还是把 A 重新设为 [1 2; 3 4; 5 6]，我再设一个 $B$为[11 12; 13 14; 15 16]，我可以新建一个矩阵 $C$，C = [A B]，这个意思就是把这两个矩阵直接连在一起，矩阵$A$ 在左边，矩阵$B$ 在右边，这样组成了 $C$矩阵，就是直接把$A$和 $B$ 合起来。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gvzin4JL-1575445908563)(https://www.github.com/OneJane/blog/raw/master/小书匠/e07db429512d4b3b5d641c52e606159d.png)]
我还可以设C = [A; B]，这里的分号表示把分号后面的东西放到下面。所以，[A;B]的作用依然还是把两个矩阵放在一起，只不过现在是上下排列，所以现在 $A$ 在上面 $B$在下面，$C$ 就是一个 6×2 矩阵。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wD2LoSxk-1575445908563)(https://www.github.com/OneJane/blog/raw/master/小书匠/7f11aa788b1b75c5a534d030b3ebc624.png)]
简单地说，分号的意思就是换到下一行，所以 C 就包括上面的A，然后换行到下面，然后在下面放上一个 $B$。

另外顺便说一下，这个[A B]命令跟 [A, B] 是一样的，这两种写法的结果是相同的。

通过以上这些操作，希望你现在掌握了怎样构建矩阵，也希望我展示的这些命令能让你很快地学会怎样把矩阵放到一起，怎样取出矩阵，并且把它们放到一起，组成更大的矩阵。

通过几句简单的代码，Octave能够很方便地很快速地帮助我们组合复杂的矩阵以及对数据进行移动。这就是移动数据这一节课。

我认为对你来讲，最好的学习方法是，下课后复习一下我键入的这些代码好好地看一看，从课程的网上把代码的副本下载下来，重新好好看看这些副本，然后自己在Octave 中把这些命令重新输一遍，慢慢开始学会使用这些命令。

当然，没有必要把这些命令都记住，你也不可能记得住。你要做的就是，了解一下你可以用哪些命令，做哪些事。这样在你今后需要编写学习算法时，如果你要找到某个Octave中的命令，你可能回想起你之前在这里学到过，然后你就可以查找课程中提供的程序副本，这样就能很轻松地找到你想使用的命令了。

计算数据

参考视频: 5 - 3 - Computing on Data (13 min).mkv

现在，你已经学会了在Octave中如何加载或存储数据，如何把数据存入矩阵等等。在这段视频中，我将介绍如何对数据进行运算，稍后我们将使用这些运算操作来实现我们的学习算法。

这是我的 Octave窗口，我现在快速地初始化一些变量。比如设置$A$为一个3×2的矩阵，设置$B$为一个3 ×2矩阵，设置$C$为2 × 2矩阵。

我想算两个矩阵的乘积，比如说 $A\times C$，我只需键入A×C，这是一个 3×2 矩阵乘以 2×2矩阵，得到这样一个3×2矩阵。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-CLAAhJoW-1575445908563)(https://www.github.com/OneJane/blog/raw/master/小书匠/8ee5c7c05865e90f75feda99b9131319.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5sG5rIMP-1575445908564)(https://www.github.com/OneJane/blog/raw/master/小书匠/38c956acb3bedf4362f40e6c5e8a692f.png)]
你也可以对每一个元素，做运算 方法是做点乘运算A.*B，这么做Octave将矩阵 $A$中的每一个元素与矩阵 $B$ 中的对应元素相乘:A.*B

这里第一个元素1乘以11得到11，第二个元素2乘以12得到24，这就是两个矩阵的元素位运算。通常来说，在Octave中点号一般用来表示元素位运算。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fdbjQ4rL-1575445908565)(https://www.github.com/OneJane/blog/raw/master/小书匠/646de38bffd4f7f6601167d0c0686970.png)]
这里是一个矩阵$A$，这里我输入A.^2，这将对矩阵$A$中每一个元素平方。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HW5b9hH1-1575445908565)(https://www.github.com/OneJane/blog/raw/master/小书匠/d456e7501d7aaa9fa2ef8a89e89fa7e1.png)]
我们设$V$为 [1; 2; 3] 是列向量，你也可以输入1./V，得到每一个元素的倒数，所以这样一来，就会分别算出 1/1 1/2 1/3。

矩阵也可以这样操作，1./A 得到$A$中每一个元素的倒数。

同样地，这里的点号还是表示对每一个元素进行操作。

我们还可以进行求对数运算，也就是对每个元素进行求对数运算。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-aUTQoIb8-1575445908566)(https://www.github.com/OneJane/blog/raw/master/小书匠/0c7c1d7726c09ffb45152cf153614003.png)]
还有自然数$e$的幂次运算，就是以$e$为底，以这些元素为幂的运算。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-13nUIck3-1575445908566)(https://www.github.com/OneJane/blog/raw/master/小书匠/a36506049248948c82e598c8c254dc31.png)]
我还可以用 abs来对 $v$ 的每一个元素求绝对值，当然这里 $v$都是正数。我们换成另一个这样对每个元素求绝对值，得到的结果就是这些非负的元素。还有$–v$，给出$v$中每个元素的相反数，这等价于 -1 乘以 $v$，一般就直接用 $-v$
就好了，其实就等于 $-1\ast v$。

还有一个技巧，比如说我们想对$v$中的每个元素都加1，那么我们可以这么做，首先构造一个3行1列的1向量，然后把这个1向量跟原来的向量相加，因此$v$向量从[1 2 3] 增至 [2 3 4]。我用了一个，length(v)命令，因此这样一来，ones(length(v) ,1) 就相当于ones(3,1)，然后我做的是v +ones(3,1)，也就是将 $v$ 的各元素都加上这些1，这样就将$v$ 的每个元素增加了1。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-iiSmod3N-1575445908567)(https://www.github.com/OneJane/blog/raw/master/小书匠/9432bbcbfde53c7e0dcb1c7317b01c0c.png)]
另一种更简单的方法是直接用 v+1，v + 1 也就等于把 $v$ 中的每一个元素都加上1。

现在，让我们来谈谈更多的操作。

矩阵$A$ 如果你想要求它的转置，那么方法是用A’,将得出 A 的转置矩阵。当然，如果我写(A')'，也就是 $A$ 转置两次，那么我又重新得到矩阵 $A$。

还有一些有用的函数，比如： a=[1 15 2 0.5]，这是一个1行4列矩阵，val=max(a)，这将返回$A$矩阵中的最大值15。

我还可以写 [val, ind] =max(a)，这将返回$A$矩阵中的最大值存入$val$，以及该值对应的索引，元素15对应的索引值为2,存入$ind$，所以 $ind=2$。

特别注意一下，如果你用命令 max(A)，$A$是一个矩阵的话，这样做就是对每一列求最大值。

我们还是用这个例子，这个 $a$ 矩阵a=[1 15 2 0.5]，如果输入a<3，这将进行逐元素的运算，所以元素小于3的返回1，否则返回0。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HYEja9uj-1575445908568)(https://www.github.com/OneJane/blog/raw/master/小书匠/fc04d42876c9d7d7bed51bade2077649.png)]
因此，返回[1 1 0 1]。也就是说，对$a$矩阵的每一个元素与3进行比较，然后根据每一个元素与3的大小关系，返回1和0表示真与假。

如果我写 find(a<3)，这将告诉我$a$ 中的哪些元素是小于3的。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-04Urji3p-1575445908568)(https://www.github.com/OneJane/blog/raw/master/小书匠/ac9ad10f115d2d1cd15a0514c8ceeafa.png)]
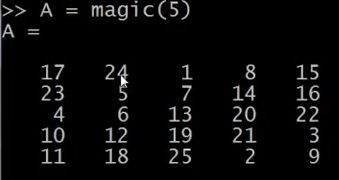
设A = magic(3)，magic 函数将返回一个矩阵，称为魔方阵或幻方 (magic squares)，它们具有以下这样的数学性质：它们所有的行和列和对角线加起来都等于相同的值。

当然据我所知，这在机器学习里基本用不上，但我可以用这个方法很方便地生成一个3行3列的矩阵，而这个魔方矩阵这神奇的方形屏幕。每一行、每一列、每一个对角线三个数字加起来都是等于同一个数。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-On1MB9X9-1575445908569)(https://www.github.com/OneJane/blog/raw/master/小书匠/f8c7f4f36183ef4b36bce427be2fce6f.png)]
在其他有用的机器学习应用中，这个矩阵其实没多大作用。

如果我输入 [r,c] = find(A>=7)，这将找出所有$A$矩阵中大于等于7的元素，因此，$r$ 和$c$分别表示行和列，这就表示，第一行第一列的元素大于等于7，第三行第二列的元素大于等于7，第二行第三列的元素大于等于7。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DuqwjIMN-1575445908570)(https://www.github.com/OneJane/blog/raw/master/小书匠/409a04487d1d7f039acfd61b3787f6aa.png)]
顺便说一句，其实我从来都不去刻意记住这个 find 函数，到底是怎么用的，我只需要会用help函数就可以了，每当我在使用这个函数，忘记怎么用的时候，我就可以用 help函数，键入 help find 来找到帮助文档。

最后再讲两个内容，一个是求和函数，这是 $a$ 矩阵：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MoGSZMgn-1575445908570)(https://www.github.com/OneJane/blog/raw/master/小书匠/d7221c981ecc7730465710a0d8b49b34.png)]
键入 sum(a)，就把 a 中所有元素加起来了。

如果我想把它们都乘起来，键入 prod(a)，prod 意思是product(乘积)，它将返回这四个元素的乘积。

floor(a) 是向下四舍五入，因此对于 $a$ 中的元素0.5将被下舍入变成0。

还有 ceil(a)，表示向上四舍五入，所以0.5将上舍入变为最接近的整数，也就是1。

键入 type(3)，这通常得到一个3×3的矩阵，如果键入 max(rand(3),rand(3))，这样做的结果是返回两个3×3的随机矩阵，并且逐元素比较取最大值。

假如我输入max(A,[],1)，这样做会得到每一列的最大值。

所以第一列的最大值就是8，第二列是9，第三列的最大值是7，这里的1表示取A矩阵第一个维度的最大值。

相对地，如果我键入max(A,[],2)，这将得到每一行的最大值，所以，第一行的最大值是等于8，第二行最大值是7，第三行是9。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5NddDwHh-1575445908571)(https://www.github.com/OneJane/blog/raw/master/小书匠/31bc524d1a19b4e9d8ea0974517a512e.png)]
所以你可以用这个方法来求得每一行或每一列的最值，另外，你要知道，默认情况下max(A)返回的是每一列的最大值，如果你想要找出整个矩阵A的最大值，你可以输入max(max(A))，或者你可以将$A$ 矩阵转成一个向量，然后键入 max(A(:))，这样做就是把 $A$ 当做一个向量，并返回 $A$向量中的最大值。

最后，让我们把 $A$设为一个9行9列的魔方阵，魔方阵具有的特性是每行每列和对角线的求和都是相等的。

这是一个9×9的魔方阵，我们来求一个 sum(A,1)，这样就得到每一列的总和，这也验证了一个9×9的魔方阵确实每一列加起来都相等，都为369。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-A50TF5MZ-1575445908571)(https://www.github.com/OneJane/blog/raw/master/小书匠/0b9753a3e10bbdce0f26c3d44d61ae26.png)]
现在我们来求每一行的和，键入sum(A,2)，这样就得到了$A$ 中每一行的和加起来还是369。

现在我们来算$A $的对角线元素的和。我们现在构造一个9×9 的单位矩阵，键入 eye(9),

然后我们要用 $A$逐点乘以这个单位矩阵，除了对角线元素外，其他元素都会得到0。

键入sum(sum(A.*eye(9))

这实际上是求得了，这个矩阵对角线元素的和确实是369。

你也可以求另一条对角线的和也是是369。

flipup/flipud 表示向上/向下翻转。

同样地，如果你想求这个矩阵的逆矩阵，键入pinv(A)，通常称为伪逆矩阵，你就把它看成是矩阵 $A$ 求逆，因此这就是 $A$矩阵的逆矩阵。

设 temp = pinv(A)，然后再用$temp$ 乘以$A$，这实际上得到的就是单位矩阵，对角线为1，其他元素为0。

如何对矩阵中的数字进行各种操作，在运行完某个学习算法之后，通常一件最有用的事情是看看你的结果，或者说让你的结果可视化，在接下来的视频中，我会非常迅速地告诉你，如何很快地画图，如何只用一两行代码，你就可以快速地可视化你的数据，这样你就能更好地理解你使用的学习算法。

绘图数据

参考视频: 5 - 4 - Plotting Data (10 min).mkv

当开发学习算法时，往往几个简单的图，可以让你更好地理解算法的内容，并且可以完整地检查下算法是否正常运行，是否达到了算法的目的。

例如在之前的视频中，我谈到了绘制成本函数$J(\theta )$，可以帮助确认梯度下降算法是否收敛。通常情况下，绘制数据或学习算法所有输出，也会启发你如何改进你的学习算法。幸运的是，Octave有非常简单的工具用来生成大量不同的图。当我用学习算法时，我发现绘制数据、绘制学习算法等，往往是我获得想法来改进算法的重要部分。在这段视频中，我想告诉你一些Octave的工具来绘制和可视化你的数据。

我们先来快速生成一些数据用来绘图。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1SqzkPWs-1575445908572)(https://www.github.com/OneJane/blog/raw/master/小书匠/4514b422525aaac1e99add67e44882ee.png)]
如果我想绘制正弦函数，这是很容易的，我只需要输入plot(t,y1)，并回车，就出现了这个图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-18PmiP8H-1575445908572)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575433328341.png)]

横轴是$t$变量，纵轴是$y1$，也就是我们刚刚所输出的正弦函数。

让我们设置$y2$

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wCJ2CaHc-1575445908573)(https://www.github.com/OneJane/blog/raw/master/小书匠/2d32a23ab895a8e765caf90a7679817e.png)]
Octave将会消除之前的正弦图，并且用这个余弦图来代替它，这里纵轴$cos(x)$从1开始，

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VBltr09z-1575445908573)(https://www.github.com/OneJane/blog/raw/master/小书匠/38969cc85853190ff3eac4f06398bc1b.png)]
如果我要同时表示正弦和余弦曲线。

我要做的就是，输入：plot(t, y1)，得到正弦函数，我使用函数hold on，hold on函数的功能是将新的图像绘制在旧的之上。

我现在绘制$y2$，输入：plot(t, y2)。

我要以不同的颜色绘制余弦函数，所以我在这里输入带引号的r绘制余弦函数，$r$表示所使用的颜色：plot(t,y2,’r’)，再加上命令xlabel('time')，
来标记X轴即水平轴，输入ylabel('value')，来标记垂直轴的值。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7Cnc9qkb-1575445908574)(https://www.github.com/OneJane/blog/raw/master/小书匠/9eb4e496f34a801fd7ba5e85c4eec66b.png)]
同时我也可以来标记我的两条函数曲线，用这个命令 legend('sin','cos')将这个图例放在右上方，表示这两条曲线表示的内容。最后输入title('myplot')，在图像的顶部显示这幅图的标题。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-p2sxStaS-1575445908574)(https://www.github.com/OneJane/blog/raw/master/小书匠/23594175efe66d5b9b1e687375a2dbda.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GUFfsnSj-1575445908575)(https://www.github.com/OneJane/blog/raw/master/小书匠/c765aeee9c53e0e77d01d1e73cabd9b4.png)]
如果你想保存这幅图像，你输入print –dpng 'myplot.png'，png是一个图像文件格式，如果你这样做了，它可以让你保存为一个文件。

Octave也可以保存为很多其他的格式，你可以键入help plot。

最后如果你想，删掉这个图像，用命令close会让这个图像关掉。

Octave也可以让你为图像标号

你键入figure(1); plot(t, y1);将显示第一张图，绘制了变量$t$ $y1$。

键入figure(2); plot(t, y2); 将显示第一张图，绘制了变量$t$ $y2$。

subplot命令，我们要使用subplot(1,2,1)，它将图像分为一个1*2的格子，也就是前两个参数，然后它使用第一个格子，也就是最后一个参数1的意思。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AV2NmdHY-1575445908575)(https://www.github.com/OneJane/blog/raw/master/小书匠/a786b8ed82ddd182f4595de2173cc84b.png)]
我现在使用第一个格子，如果键入plot(t,y1)，现在这个图显示在第一个格子。如果我键入subplot(1,2,2)，那么我就要使用第二个格子，键入plot(t,y2)；现在y2显示在右边，也就是第二个格子。

最后一个命令，你可以改变轴的刻度，比如改成[0.5 1 -1 1]，输入命令：axis([0.5 1 -1 1])也就是设置了右边图的$x$轴和$y$轴的范围。具体而言，它将右图中的横轴的范围调整至0.5到1，竖轴的范围为-1到1。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Ym6R6S99-1575445908576)(https://www.github.com/OneJane/blog/raw/master/小书匠/f13993f4784d01e7da769b4ec2545cd7.png)]
你不需要记住所有这些命令，如果你需要改变坐标轴，或者需要知道axis命令，你可以用Octave中用help命令了解细节。

最后，还有几个命令。

Clf（清除一幅图像）。

让我们设置A等于一个5×5的magic方阵：

我有时用一个巧妙的方法来可视化矩阵，也就是imagesc(A)命令，它将会绘制一个5*5的矩阵，一个5*5的彩色格图，不同的颜色对应A矩阵中的不同值。

我还可以使用函数colorbar，让我用一个更复杂的命令 imagesc(A)，colorbar，colormap gray。这实际上是在同一时间运行三个命令：运行imagesc，然后运行，colorbar，然后运行colormap gray。

它生成了一个颜色图像，一个灰度分布图，并在右边也加入一个颜色条。所以这个颜色条显示不同深浅的颜色所对应的值。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dxhUWeRW-1575445908577)(https://www.github.com/OneJane/blog/raw/master/小书匠/881986ec5af9d86b6b14b260fb3b3618.png)]
你可以看到在不同的方格，它对应于一个不同的灰度。

输入imagesc(magic(15))，colorbar，colormap gray

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-REXsciNs-1575445908577)(https://www.github.com/OneJane/blog/raw/master/小书匠/22a9a9536d4db17b6d64603fb54dce9e.png)]
这将会是一幅15*15的magic方阵值的图。

最后，总结一下这段视频。你看到我所做的是使用逗号连接函数调用。如果我键入$a=1$,$b=2$,$c=3$然后按Enter键，其实这是将这三个命令同时执行，或者是将三个命令一个接一个执行，它将输出所有这三个结果。

这很像$a=1$; $b=2$;$c=3$;如果我用分号来代替逗号，则没有输出出任何东西。

这里我们称之为逗号连接的命令或函数调用。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lka49NAd-1575445908578)(https://www.github.com/OneJane/blog/raw/master/小书匠/c0e8b7a19ced9a1dd006ed87d6323c9b.png)]
用逗号连接是另一种Octave中更便捷的方式，将多条命令例如imagesc colorbar colormap，将这多条命令写在同一行中。

现在你知道如何绘制Octave中不同的图像，在下面的视频中，我将告诉你怎样在Octave中，写控制语句，比如if while for语句，并且定义和使用函数。

控制语句：for，while，if语句

参考视频: 5 - 5 - Control Statements_ for, while, if statements (13 min).mkv

在这段视频中，我想告诉你怎样为你的 Octave 程序写控制语句。诸如：“for” “while” “if” 这些语句，并且如何定义和使用方程。

我先告诉你如何使用 “for” 循环。

首先，我要将 $v$ 值设为一个10行1列的零向量。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZIIEO5rx-1575445908578)(https://www.github.com/OneJane/blog/raw/master/小书匠/26a912d550af9fd43a7ae62e3b610e97.png)]
接着我要写一个 “for" 循环，让 $i$ 等于 1 到 10，写出来就是 i = 1:10。我要设$ v(i)$的值等于 2 的 $i$ 次方，循环最后写上“end”。

向量$v$ 的值就是这样一个集合 2的一次方、2的二次方，依此类推。这就是我的 $i$ 等于 1 到 10的语句结构，让 $i$ 遍历 1 到 10的值。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TZB9wOD9-1575445908579)(https://www.github.com/OneJane/blog/raw/master/小书匠/890f6ea8f857f22002f98c20d52b3bb8.png)]
另外，你还可以通过设置你的 indices (索引) 等于 1一直到10，来做到这一点。这时indices 就是一个从1到10的序列。

你也可以写 i = indices，这实际上和我直接把 i 写到 1 到 10 是一样。你可以写 disp(i)，也能得到一样的结果。所以 这就是一个 “for” 循环。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-afx82mnC-1575445908579)(https://www.github.com/OneJane/blog/raw/master/小书匠/fc956ae1291dc7d3b819e471d1962398.png)]
如果你对 “break” 和 “continue” 语句比较熟悉，Octave里也有 “break” 和 “continue”语句，你也可以在 Octave环境里使用那些循环语句。

但是首先让我告诉你一个 while 循环是如何工作的：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-O8sK45qb-1575445908580)(https://www.github.com/OneJane/blog/raw/master/小书匠/1b37f81896a59145576ae996c9dd4d16.png)]
这是什么意思呢：我让 $i$ 取值从 1 开始，然后我要让 $v(i)$ 等于 100，再让 $i$ 递增 1，直到$i$ 大于 5停止。

现在来看一下结果，我现在已经取出了向量的前五个元素，把他们用100覆盖掉，这就是一个while循环的句法结构。

现在我们来分析另外一个例子：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0KpkEJFo-1575445908580)(https://www.github.com/OneJane/blog/raw/master/小书匠/279cfbda6b4d9a2ced1332f086db4d9e.png)]
这里我将向你展示如何使用break语句。比方说 v(i) = 999，然后让 i = i+1，当 $i$ 等于6的时候 break (停止循环)，结束 (end)。

当然这也是我们第一次使用一个 if 语句，所以我希望你们可以理解这个逻辑，让 $i$ 等于1 然后开始下面的增量循环，while语句重复设置 $v(i)$ 等于999，不断让$i$增加，然后当 $i$ 达到6，做一个中止循环的命令，尽管有while循环，语句也就此中止。所以最后的结果是取出向量 $v$ 的前5个元素，并且把它们设置为999。

所以，这就是if 语句和 while 语句的句法结构。并且要注意要有end，上面的例子里第一个 end 结束的是 if
语句，第二个 end 结束的是 while 语句。

现在让我告诉你使用 if-else 语句：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-aflKNoqx-1575445908581)(https://www.github.com/OneJane/blog/raw/master/小书匠/3fce4367c960bb6fbc492a3b8f9ddc5d.png)]
最后，提醒一件事：如果你需要退出 Octave，你可以键入exit命令然后回车就会退出 Octave，或者命令quit也可以。

最后，让我们来说说函数 (functions)，如何定义和调用函数。

我在桌面上存了一个预先定义的文件名为 “squarethisnumber.m”，这就是在 Octave 环境下定义的函数。

让我们打开这个文件。请注意，我使用的是微软的写字板程序来打开这个文件，我只是想建议你，如果你也使用微软的Windows系统，那么可以使用写字板程序，而不是记事本来打开这些文件。如果你有别的什么文本编辑器也可以，记事本有时会把代码的间距弄得很乱。如果你只有记事本程序，那也能用。我建议你用写字板或者其他可以编辑函数的文本编辑器。

现在我们来说如何在 Octave 里定义函数：

这个文件只有三行：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WIkwIVsR-1575445908581)(https://www.github.com/OneJane/blog/raw/master/小书匠/247f96f4e7ab7a259ac9ef1eebe0b503.png)]
第一行写着 function y = squareThisNumber(x)，这就告诉 Octave，我想返回一个 y值，我想返回一个值，并且返回的这个值将被存放于变量 $y$ 里。另外，它告诉了Octave这个函数有一个参数，就是参数 $x$，还有定义的函数体，也就是 $y$ 等于 $x$ 的平方。

还有一种更高级的功能，这只是对那些知道“search path (搜索路径)”这个术语的人使用的。所以如果你想要修改
Octave的搜索路径，你可以把下面这部分作为一个进阶知识，或者选学材料，仅适用于那些熟悉编程语言中搜索路径概念的同学。

你可以使用addpath 命令添加路径，添加路径“C:\Users\ang\desktop”将该目录添加到Octave的搜索路径，这样即使你跑到其他路径底下，Octave依然知道会在 Users\ang\desktop目录下寻找函数。这样，即使我现在在不同的目录下，它仍然知道在哪里可以找到“SquareThisNumber” 这个函数。

但是，如果你不熟悉搜索路径的概念，不用担心，只要确保在执行函数之前，先用 cd命令设置到你函数所在的目录下，实际上也是一样的效果。

Octave还有一个其他许多编程语言都没有的概念，那就是它可以允许你定义一个函数，使得返回值是多个值或多个参数。这里就是一个例子，定义一个函数叫：

“SquareAndCubeThisNumber(x)” ($x$的平方以及$x$的立方)

这说的就是函数返回值是两个： $y1$ 和 $y2$，接下来就是$y1$是被平方后的结果，$y2$是被立方后的结果，这就是说，函数会真的返回2个值。

有些同学可能会根据你使用的编程语言，比如你们可能熟悉的C或C++，通常情况下，认为作为函数返回值只能是一个值，但Octave 的语法结构就不一样，可以返回多个值。

如果我键入 [a,b] = SquareAndCubeThisNumber(5)，然后，$a$就等于25，$b$ 就等于5的立方125。

所以说如果你需要定义一个函数并且返回多个值，这一点常常会带来很多方便。

最后，我来给大家演示一下一个更复杂一点的函数的例子。

比方说，我有一个数据集，像这样，数据点为[1,1], [2,2],[3,3]，我想做的事是定义一个 Octave 函数来计算代价函数 $J(\theta )$，就是计算不同 $\theta$值所对应的代价函数值$J$。

首先让我们把数据放到 Octave 里，我把我的矩阵设置为X = [1 1; 1 2; 1 3];

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8wu3x1J7-1575445908582)(https://www.github.com/OneJane/blog/raw/master/小书匠/3c857152ef3f0d6b374e4863289d1c60.png)]
请仔细看一下这个函数的定义，确保你明白了定义中的每一步。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VtT0K32J-1575445908582)(https://www.github.com/OneJane/blog/raw/master/小书匠/e01d6da07890e32d46d0616741a3fe64.png)]
现在当我在 Octave 里运行时，我键入 J = costFunctionJ (X, y, theta)，它就计算出 $J$等于0，这是因为如果我的数据集$x$ 为 [1;2;3]， $y$ 也为 [1;2;3] 然后设置 ${\theta }_0$ 等于0，${\theta }_1$等于1，这给了我恰好45度的斜线，这条线是可以完美拟合我的数据集的。

而相反地，如果我设置$\theta$ 等于[0;0]，那么这个假设就是0是所有的预测值，和刚才一样，设置${\theta }_0$ = 0，${\theta }_1$也等于0，然后我计算的代价函数，结果是2.333。实际上，他就等于1的平方，也就是第一个样本的平方误差，加上2的平方，加上3的平方，然后除以$2m$，也就是训练样本数的两倍，这就是2.33。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8sxVm35Q-1575445908583)(https://www.github.com/OneJane/blog/raw/master/小书匠/885b5d19c33f545292ccc1b69976c789.png)]
因此这也反过来验证了我们这里的函数，计算出了正确的代价函数。这些就是我们用简单的训练样本尝试的几次试验，这也可以作为我们对定义的代价函数$J$进行了完整性检查。确实是可以计算出正确的代价函数的。至少基于这里的 $x$和 $y$是成立的。也就是我们这几个简单的训练集，至少是成立的。

现在你知道如何在 Octave 环境下写出正确的控制语句，比如 for 循环、while 循环和 if语句，以及如何定义和使用函数。

在接下来的Octave 教程视频里，我会讲解一下向量化，这是一种可以使你的 Octave程序运行非常快的思想。

向量化

参考视频: 5 - 6 - Vectorization (14 min).mkv

在这段视频中，我将介绍有关向量化的内容，无论你是用Octave，还是别的语言，比如MATLAB或者你正在用Python、NumPy 或 Java C C++，所有这些语言都具有各种线性代数库，这些库文件都是内置的，容易阅读和获取，他们通常写得很好，已经经过高度优化，通常是数值计算方面的博士或者专业人士开发的。

而当你实现机器学习算法时，如果你能好好利用这些线性代数库，或者数值线性代数库，并联合调用它们，而不是自己去做那些函数库可以做的事情。如果是这样的话，那么通常你会发现：首先，这样更有效，也就是说运行速度更快，并且更好地利用你的计算机里可能有的一些并行硬件系统等等；其次，这也意味着你可以用更少的代码来实现你需要的功能。因此，实现的方式更简单，代码出现问题的有可能性也就越小。

举个具体的例子：与其自己写代码做矩阵乘法。如果你只在Octave中输入$a$乘以$b$就是一个非常有效的两个矩阵相乘的程序。有很多例子可以说明，如果你用合适的向量化方法来实现，你就会有一个简单得多，也有效得多的代码。

让我们来看一些例子：这是一个常见的线性回归假设函数：$h_{\theta }(x)=\sum _{j=0}^n{\theta }_j{x}_j$

如果你想要计算$h_{\theta }(x)$ ，注意到右边是求和，那么你可以自己计算$j=0$ 到$ j = n$ 的和。但换另一种方式来想想，把 $h_{\theta }(x)$ 看作${\theta }^{T}x$，那么你就可以写成两个向量的内积，其中$\theta$就是${\theta }_0$、${\theta }_1$、${\theta }_2$，如果你有两个特征量，如果 $n=2$，并且如果你把 $x$ 看作$x_0$、$x_1$、$x_2$，这两种思考角度，会给你两种不同的实现方式。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qEEKN8Sg-1575445908583)(https://www.github.com/OneJane/blog/raw/master/小书匠/7fefb92d8680e4a15f947cd2ca24a9ac.png)]
比如说，这是未向量化的代码实现方式：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ULfZD5d0-1575445908584)(https://www.github.com/OneJane/blog/raw/master/小书匠/125c07019cb39675085fe3b80b85fca5.png)]
计算$h_{\theta }(x)$是未向量化的，我们可能首先要初始化变量 $prediction$ 的值为0.0，而这个变量$prediction$ 的最终结果就是$h_{\theta }(x)$，然后我要用一个 for 循环，$j$ 取值 0 到$n+1$，变量$prediction$ 每次就通过自身加上$ theta(j) $乘以 $x(j)$更新值，这个就是算法的代码实现。

顺便我要提醒一下，这里的向量我用的下标是0，所以我有${\theta }_0$、${\theta }_1$、${\theta }_2$，但因为MATLAB的下标从1开始，在 MATLAB 中${\theta }_0$，我们可能会用 $theta(1)$ 来表示，这第二个元素最后就会变成，$theta(2$) 而第三个元素，最终可能就用$theta(3)$表示，因为MATLAB中的下标从1开始，这就是为什么这里我的 for 循环，$j$取值从 1 直到$n+1$，而不是从 0 到 $n$。这是一个未向量化的代码实现方式，我们用一个 for 循环对 $n$ 个元素进行加和。

作为比较，接下来是向量化的代码实现：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gOZgZgSY-1575445908584)(https://www.github.com/OneJane/blog/raw/master/小书匠/829e153c119919f80c058d1bc703a08b.png)]
你把x和$\theta$看做向量，而你只需要令变量$prediction$等于$theta$转置乘以$x$，你就可以这样计算。与其写所有这些for循环的代码，你只需要一行代码，这行代码就是利用 Octave 的高度优化的数值，线性代数算法来计算两个向量$\theta$以及$x$的内积，这样向量化的实现更简单，它运行起来也将更加高效。这就是 Octave 所做的而向量化的方法，在其他编程语言中同样可以实现。

让我们来看一个C++ 的例子：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4meAOx6c-1575445908585)(https://www.github.com/OneJane/blog/raw/master/小书匠/987fc9372da3b167fd16d7a19722405b.png)]
与此相反，使用较好的C++ 数值线性代数库，你可以写出像右边这样的代码，因此取决于你的数值线性代数库的内容。你只需要在C++ 中将两个向量相乘，根据你所使用的数值和线性代数库的使用细节的不同，你最终使用的代码表达方式可能会有些许不同，但是通过一个库来做内积，你可以得到一段更简单、更有效的代码。

现在，让我们来看一个更为复杂的例子，这是线性回归算法梯度下降的更新规则：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ya744BqB-1575445908585)(https://www.github.com/OneJane/blog/raw/master/小书匠/6ad266a30f955db5b905905670aabfc5.png)]
我们用这条规则对$ j$ 等于 0、1、2等等的所有值，更新对象${\theta }_j$，我只是用${\theta }_0$、${\theta }_1$、${\theta }_2$来写方程，假设我们有两个特征量，所以$n$等于2，这些都是我们需要对${\theta }_0$、${\theta }_1$、${\theta }_2$进行更新，这些都应该是同步更新，我们用一个向量化的代码实现，这里是和之前相同的三个方程，只不过写得小一点而已。

你可以想象实现这三个方程的方式之一，就是用一个 for 循环，就是让 $j$等于0、等于1、等于2，来更新${\theta }_j$。但让我们用向量化的方式来实现，看看我们是否能够有一个更简单的方法。基本上用三行代码或者一个for 循环，一次实现这三个方程。让我们来看看怎样能用这三步，并将它们压缩成一行向量化的代码来实现。做法如下：

我打算把$\theta$看做一个向量，然后我用$\theta$-$\alpha$ 乘以某个别的向量$\delta$ 来更新$\theta$。

这里的 $\delta$ 等于

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JeKiV2pZ-1575445908586)(https://www.github.com/OneJane/blog/raw/master/小书匠/fa662ec6d5703d85c314f5e4792a7468.png)]
让我解释一下是怎么回事：我要把$\theta$看作一个向量，有一个 $n+1$ 维向量，$\alpha$ 是一个实数，$\delta$在这里是一个向量。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cS5sZDyg-1575445908587)(https://www.github.com/OneJane/blog/raw/master/小书匠/20bc912bae44e66125f8bfcec6e720c7.png)]
所以这个减法运算是一个向量减法，因为 $\alpha$ 乘以 δ是一个向量，所以$\theta$就是$\theta$ - $\alpha \delta$得到的向量。

那么什么是向量 $\delta$ 呢 ?

$X^{(i)}$是一个向量

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-y1Uhigc6-1575445908587)(https://www.github.com/OneJane/blog/raw/master/小书匠/0a03d239f2f1d1af057d492bcce276f4.png)]
你就会得到这些不同的式子，然后作加和。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ipioHsbd-1575445908588)(https://www.github.com/OneJane/blog/raw/master/小书匠/8d10103bf172a889090690a00037ffa1.png)]
实际上，在以前的一个小测验，如果你要解这个方程，我们说过为了向量化这段代码，我们会令u = 2v +5w因此，我们说向量$u$等于2乘以向量$v$加上5乘以向量$w$。用这个例子说明，如何对不同的向量进行相加，这里的求和是同样的道理。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-H4ko0ZJN-1575445908589)(https://www.github.com/OneJane/blog/raw/master/小书匠/c84012101afc6836a3396893695d9669.png)]
这就是为什么我们能够向量化地实现线性回归。

所以，我希望步骤是有逻辑的。请务必看视频，并且保证你确实能理解它。如果你实在不能理解它们数学上等价的原因，你就直接实现这个算法，也是能得到正确答案的。所以即使你没有完全理解为何是等价的，如果只是实现这种算法，你仍然能实现线性回归算法。如果你能弄清楚为什么这两个步骤是等价的，那我希望你可以对向量化有一个更好的理解，如果你在实现线性回归的时候，使用一个或两个以上的特征量。

有时我们使用几十或几百个特征量来计算线性归回，当你使用向量化地实现线性回归，通常运行速度就会比你以前用你的for循环快的多，也就是自己写代码更新${\theta }_0$、${\theta }_1$、${\theta }_2$。

因此使用向量化实现方式，你应该是能够得到一个高效得多的线性回归算法。而当你向量化我们将在之后的课程里面学到的算法，这会是一个很好的技巧，无论是对于Octave 或者一些其他的语言 如C++、Java 来让你的代码运行得更高效。

逻辑回归(Logistic Regression)

分类问题

参考文档: 6 - 1 - Classification (8 min).mkv

在这个以及接下来的几个视频中，开始介绍分类问题。

在分类问题中，你要预测的变量 $y$ 是离散的值，我们将学习一种叫做逻辑回归 (Logistic Regression) 的算法，这是目前最流行使用最广泛的一种学习算法。

在分类问题中，我们尝试预测的是结果是否属于某一个类（例如正确或错误）。分类问题的例子有：判断一封电子邮件是否是垃圾邮件；判断一次金融交易是否是欺诈；之前我们也谈到了肿瘤分类问题的例子，区别一个肿瘤是恶性的还是良性的。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ae96aZzD-1575445908589)(https://www.github.com/OneJane/blog/raw/master/小书匠/a77886a6eff0f20f9d909975bb69a7ab.png)]
我们从二元的分类问题开始讨论。

我们将因变量(dependent variable)可能属于的两个类分别称为负向类（negative class）和正向类（positive class），则因变量$y\in 0,1$ ，其中 0 表示负向类，1 表示正向类。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-l4knw1tI-1575445908589)(https://www.github.com/OneJane/blog/raw/master/小书匠/1575441014185.png)]

如果我们要用线性回归算法来解决一个分类问题，对于分类， $y$ 取值为 0 或者1，但如果你使用的是线性回归，那么假设函数的输出值可能远大于 1，或者远小于0，即使所有训练样本的标签 $y$ 都等于 0 或 1。尽管我们知道标签应该取值0 或者1，但是如果算法得到的值远大于1或者远小于0的话，就会感觉很奇怪。所以我们在接下来的要研究的算法就叫做逻辑回归算法，这个算法的性质是：它的输出值永远在0到 1 之间。

顺便说一下，逻辑回归算法是分类算法，我们将它作为分类算法使用。有时候可能因为这个算法的名字中出现了“回归”使你感到困惑，但逻辑回归算法实际上是一种分类算法，它适用于标签 $y$ 取值离散的情况，如：1 0 0 1。

在接下来的视频中，我们将开始学习逻辑回归算法的细节。

假说表示

参考视频: 6 - 2 - Hypothesis Representation (7 min).mkv

在这段视频中，我要给你展示假设函数的表达式，也就是说，在分类问题中，要用什么样的函数来表示我们的假设。此前我们说过，希望我们的分类器的输出值在0和1之间，因此，我们希望想出一个满足某个性质的假设函数，这个性质是它的预测值要在0和1之间。

回顾在一开始提到的乳腺癌分类问题，我们可以用线性回归的方法求出适合数据的一条直线：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MDtLI4am-1575445908590)(https://www.github.com/OneJane/blog/raw/master/小书匠/29c12ee079c079c6408ee032870b2683.jpg)]
根据线性回归模型我们只能预测连续的值，然而对于分类问题，我们需要输出0或1，我们可以预测：

当$h_{\theta }\left(x\right)>=0.5$时，预测 $y=1$。

当$h_{\theta }\left(x\right)<0.5$时，预测 $y=0$ 。

对于上图所示的数据，这样的一个线性模型似乎能很好地完成分类任务。假使我们又观测到一个非常大尺寸的恶性肿瘤，将其作为实例加入到我们的训练集中来，这将使得我们获得一条新的直线。

这时，再使用0.5作为阀值来预测肿瘤是良性还是恶性便不合适了。可以看出，线性回归模型，因为其预测的值可以超越[0,1]的范围，并不适合解决这样的问题。

我们引入一个新的模型，逻辑回归，该模型的输出变量范围始终在0和1之间。
逻辑回归模型的假设是： $h_{\theta }\left(x\right)=g\left({\theta }^{T}X\right)$
其中：
$X$ 代表特征向量
$g$ 代表逻辑函数（logistic function)是一个常用的逻辑函数为S形函数（Sigmoid function），公式为： $g\left(z\right)=\frac{1}{1+e^{-z}}$。

python代码实现：

import numpy as np
    
def sigmoid(z):
    
   return 1 / (1 + np.exp(-z))

该函数的图像为：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LXMMGqXF-1575445908591)(https://www.github.com/OneJane/blog/raw/master/小书匠/1073efb17b0d053b4f9218d4393246cc.jpg)]
合起来，我们得到逻辑回归模型的假设：

对模型的理解： $g\left(z\right)=\frac{1}{1+e^{-z}}$。

$h_{\theta }\left(x\right)$的作用是，对于给定的输入变量，根据选择的参数计算输出变量=1的可能性（estimated probablity）即$h_{\theta }\left(x\right)=P\left(y=1|x;\theta \right)$
例如，如果对于给定的$x$，通过已经确定的参数计算得出$h_{\theta }\left(x\right)=0.7$，则表示有70%的几率$y$为正向类，相应地$y$为负向类的几率为1-0.7=0.3。

判定边界

参考视频: 6 - 3 - Decision Boundary (15 min).mkv

现在讲下决策边界(decision boundary)的概念。这个概念能更好地帮助我们理解逻辑回归的假设函数在计算什么。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cKTlxI7n-1575445908591)(https://www.github.com/OneJane/blog/raw/master/小书匠/6590923ac94130a979a8ca1d911b68a3.png)]
在逻辑回归中，我们预测：

当$h_{\theta }\left(x\right)>=0.5$时，预测 $y=1$。

当$h_{\theta }\left(x\right)<0.5$时，预测 $y=0$ 。

根据上面绘制出的 S 形函数图像，我们知道当

$z=0$ 时 $g(z)=0.5$

$z>0$ 时 $g(z)>0.5$

$z<0$ 时 $g(z)<0.5$

又 $z={\theta }^{T}x$ ，即：
${\theta }^{T}x>=0$ 时，预测 $y=1$
${\theta }^{T}x<0$ 时，预测 $y=0$

现在假设我们有一个模型：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-p20RzRU2-1575445908592)(https://www.github.com/OneJane/blog/raw/master/小书匠/58d098bbb415f2c3797a63bd870c3b8f.png)]
并且参数$\theta$ 是向量[-3 1 1]。 则当$-3+x_1+x_2\ge 0$，即$x_1+x_2\ge 3$时，模型将预测 $y=1$。
我们可以绘制直线$x_1+x_2=3$，这条线便是我们模型的分界线，将预测为1的区域和预测为 0的区域分隔开。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oZecN4k7-1575445908592)(https://www.github.com/OneJane/blog/raw/master/小书匠/f71fb6102e1ceb616314499a027336dc.jpg)]
假使我们的数据呈现这样的分布情况，怎样的模型才能适合呢？

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XsiU1I9Q-1575445908593)(https://www.github.com/OneJane/blog/raw/master/小书匠/197d605aa74bee1556720ea248bab182.jpg)]
因为需要用曲线才能分隔 $y=0$ 的区域和 $y=1$ 的区域，我们需要二次方特征：$h_{\theta }\left(x\right)=g\left({\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_1^2+{\theta }_4{x}_2^2\right)$是[-1 0 0 1 1]，则我们得到的判定边界恰好是圆点在原点且半径为1的圆形。

我们可以用非常复杂的模型来适应非常复杂形状的判定边界。

代价函数

参考视频: 6 - 4 - Cost Function (11 min).mkv

在这段视频中，我们要介绍如何拟合逻辑回归模型的参数$\theta$。具体来说，我要定义用来拟合参数的优化目标或者叫代价函数，这便是监督学习问题中的逻辑回归模型的拟合问题。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2LLeV2Lj-1575445908593)(https://www.github.com/OneJane/blog/raw/master/小书匠/f23eebddd70122ef05baa682f4d6bd0f.png)]
对于线性回归模型，我们定义的代价函数是所有模型误差的平方和。理论上来说，我们也可以对逻辑回归模型沿用这个定义，但是问题在于，当我们将$h_{\theta }\left(x\right)=\frac{1}{1+e^{-{\theta }^{T}x}}$带入到这样定义了的代价函数中时，我们得到的代价函数将是一个非凸函数（non-convexfunction）。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-66EYs3PR-1575445908593)(https://www.github.com/OneJane/blog/raw/master/小书匠/8b94e47b7630ac2b0bcb10d204513810.jpg)]
这意味着我们的代价函数有许多局部最小值，这将影响梯度下降算法寻找全局最小值。

线性回归的代价函数为：$J\left(\theta \right)=\frac{1}{m}\sum _{i=1}^m\frac{1}{2}{\left(h_{\theta }\left(x^{\left(i\right)}\right)-y^{\left(i\right)}\right)}^2$ 。
我们重新定义逻辑回归的代价函数为：$J\left(\theta \right)=\frac{1}{m}\sum _{i=1}^{m}Cost\left(h_{\theta }\left(x^{\left(i\right)}\right),y^{\left(i\right)}\right)$，其中

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-awSigNgk-1575445908594)(https://www.github.com/OneJane/blog/raw/master/小书匠/54249cb51f0086fa6a805291bf2639f1.png)]
$h_{\theta }\left(x\right)$与 $Cost\left(h_{\theta }\left(x\right),y\right)$之间的关系如下图所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-arcU9KlH-1575445908594)(https://www.github.com/OneJane/blog/raw/master/小书匠/ffa56adcc217800d71afdc3e0df88378.jpg)]
这样构建的$Cost\left(h_{\theta }\left(x\right),y\right)$函数的特点是：当实际的 $y=1$ 且$h_{\theta }\left(x\right)$也为 1 时误差为 0，当 $y=1$ 但$h_{\theta }\left(x\right)$不为1时误差随着$h_{\theta }\left(x\right)$变小而变大；当实际的 $y=0$ 且$h_{\theta }\left(x\right)$也为 0 时代价为 0，当$y=0$ 但$h_{\theta }\left(x\right)$不为 0时误差随着 $h_{\theta }\left(x\right)$的变大而变大。
将构建的 $Cost\left(h_{\theta }\left(x\right),y\right)$简化如下：
$Cost\left(h_{\theta }\left(x\right),y\right)=-y\times log\left(h_{\theta }\left(x\right)\right)-(1-y)\times log\left(1-h_{\theta }\left(x\right)\right)$
带入代价函数得到：
$J\left(\theta \right)=\frac{1}{m}\sum _{i=1}^m[-y^{(i)}\log \left(h_{\theta }\left(x^{(i)}\right)\right)-\left(1-y^{(i)}\right)\log \left(1-h_{\theta }\left(x^{(i)}\right)\right)]$
即：$J\left(\theta \right)=-\frac{1}{m}\sum _{i=1}^m[y^{(i)}\log \left(h_{\theta }\left(x^{(i)}\right)\right)+\left(1-y^{(i)}\right)\log \left(1-h_{\theta }\left(x^{(i)}\right)\right)]$

Python代码实现：

import numpy as np
    
def cost(theta, X, y):
    
  theta = np.matrix(theta)
  X = np.matrix(X)
  y = np.matrix(y)
  first = np.multiply(-y, np.log(sigmoid(X* theta.T)))
  second = np.multiply((1 - y), np.log(1 - sigmoid(X* theta.T)))
  return np.sum(first - second) / (len(X))

在得到这样一个代价函数以后，我们便可以用梯度下降算法来求得能使代价函数最小的参数了。算法为：

Repeat {
${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J(\theta )$
(simultaneously update all )
}

求导后得到：

Repeat {
${\theta }_j:={\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^m\left(h_{\theta }\left(x^{\left(i\right)}\right)-y^{\left(i\right)}\right)x_j^{(i)}$
(simultaneously update all )
}

在这个视频中，我们定义了单训练样本的代价函数，凸性分析的内容是超出这门课的范围的，但是可以证明我们所选的代价值函数会给我们一个凸优化问题。代价函数$J(\theta )$会是一个凸函数，并且没有局部最优值。

推导过程：

$J\left(\theta \right)=-\frac{1}{m}\sum _{i=1}^m[y^{(i)}\log \left(h_{\theta }\left(x^{(i)}\right)\right)+\left(1-y^{(i)}\right)\log \left(1-h_{\theta }\left(x^{(i)}\right)\right)]$
考虑：
$h_{\theta }\left(x^{(i)}\right)=\frac{1}{1+e^{-{\theta }^T{x}^{(i)}}}$
则：
$y^{(i)}\log \left(h_{\theta }\left(x^{(i)}\right)\right)+(1-$