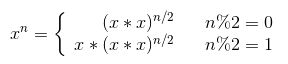- 11. 旋转数组的最小数字
- 12. 矩阵中的路径
- 13. 机器人的运动范围
- 14. 剪绳子
- 15. 二进制中 1 的个数
- 16. 数值的整数次方
- 17. 打印从 1 到最大的 n 位数
- 18.1 在 O(1) 时间内删除链表节点
- 18.2 删除链表中重复的结点
- 19. 正则表达式匹配
- 20. 表示数值的字符串
阅前需知
1.本文部分内容参考剑指 offer 题解,如有侵权,请告知。其他内容均属原创,转载请告知。
2.本文示例代码中给一些类增加了一些类扩展,因篇幅原因,未在文中写出,详情见项目源码,地址文末有提供。
3.阅读本文之前需要先了解节点,链表,栈,二叉树的实现。详情见如下文章连接。
4.因为 OC 中没有栈,链表节点,链表的概念,所以本项目自定义了栈,链表节点,链表类。
5.因技术水平有限,如有错误,欢迎指正。
- iOS - 节点,链表的实现
- iOS - 栈的实现
- iOS - 二叉树,哈希表的实现
以下是通过 OC 语法实现
11.旋转数组的最小数字
题目描述
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。
例如数组 {3, 4, 5, 1, 2} 为 {1, 2, 3, 4, 5} 的一个旋转,该数组的最小值为 1。
解题思路
在一个有序数组中查找一个元素可以用二分查找,二分查找也称为折半查找,每次都能将查找区间减半,这种折半特性的算法时间复杂度都为 O(logN)。
本题可以修改二分查找算法进行求解:
- 当 nums[m] <= nums[h] 的情况下,说明解在 [l, m] 之间,此时令 h = m;
- 否则解在 [m + 1, h] 之间,令 l = m + 1。
详细代码如下
/** 折半查找最小值 */
+ (int)minNumberInRotateArray:(NSArray *)nums {
if (nums.count == 0) {
return 0;
}
int l = 0, h = (int)nums.count - 1;
while (l < h) {
int m = l + (h - l) / 2; // 中间值
if ([nums[m] intValue] <= [nums[h] intValue]) {
h = m;
} else {
l = m + 1;
}
}
return [nums[l] intValue];
}
测试案例代码
// 11.1 折半查询
- (void)minNumberInRotateArray {
int number = [MinNumberInRotateArray minNumberInRotateArray:@[@1,@4,@8,@11,@20]];
NSLog(@"number = %d",number);
}
运行结果
11.2 重复数字
如果数组元素允许重复的话,那么就会出现一个特殊的情况:nums[l] == nums[m] == nums[h],那么此时无法确定解在哪个区间,需要切换到顺序查找。例如对于数组 {1,1,1,0,1},l、m 和 h 指向的数都为 1,此时无法知道最小数字 0 在哪个区间。
详细代码如下
+ (int)minNumberInRotateArray2:(NSArray *)nums {
if (nums.count == 0) {
return 0;
}
int l = 0, h = (int)nums.count - 1;
while (l < h) {
int m = l + (h - l) / 2; // 中间值
if (nums[l] == nums[m] && nums[m] == nums[h]) { // 三者相等
return [self minNumber:nums l:l h:h];
} else if ([nums[m] intValue] <= [nums[h] intValue]) {
h = m;
} else {
l = m + 1;
}
}
return [nums[l] intValue];
}
+ (int)minNumber:(NSArray *)nums l:(int)l h:(int)h {
for (int i = l; i < h; i++) {
if ([nums[i] intValue] > [nums[i + 1] intValue]) {
return [nums[i + 1] intValue];
}
}
return [nums[l] intValue];
}
测试案例代码
// 11.2 折半查询
- (void)minNumberInRotateArray2 {
int number = [MinNumberInRotateArray minNumberInRotateArray2:@[@3,@4,@2,@1,@3]];
NSLog(@"number = %d",number);
}
运行结果
12.矩阵中的路径
题目描述
请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向左,向右,向上,向下移动一个格子。如果一条路径经过了矩阵中的某一个格子,则该路径不能再进入该格子。
例如下面的矩阵包含了一条 bfce 路径。
详细代码如下
- MatrixHasPath.h
/**
矩阵中的路径
*/
@interface MatrixHasPath : NSObject
- (BOOL)hasPath:(NSString *)oriStr rows:(int)rows cols:(int)cols str:(NSString *)str;
@end
- MatrixHasPath.m
@implementation MatrixHasPath {
NSArray *_next;
int _rows;
int _cols;
}
- (instancetype)init {
self = [super init];
if (self) {
// 上 下 左 右 四个方向
_next = @[@[@0,@(-1)],@[@0,@1],@[@(-1),@0],@[@1,@0]];
}
return self;
}
- (BOOL)hasPath:(NSString *)oriStr rows:(int)rows cols:(int)cols str:(NSString *)str {
if (rows == 0 || cols == 0) {
return NO;
}
_rows = rows;
_cols = cols;
// 1.先构造一个二维数组,数值都填充为0,表示没有遍历过
NSMutableArray *marked = [NSMutableArray array];
for (int i = 0; i < _rows; i++) {
NSMutableArray *firstArrM = [NSMutableArray array];
for (int j = 0; j < _cols; j++) {
[firstArrM addObject:@0];
}
[marked addObject:firstArrM];
}
// 2.构造一个矩阵 array-完整路径的数组,即a,b,t,g,c...h,并且是一个 rows * cols 的矩阵
NSMutableArray *oriStrs = [NSMutableArray array];
for (int i = 0; i < oriStr.length; i++) {
[oriStrs addObject:[oriStr substringWithRange:NSMakeRange(i, 1)]];
}
NSMutableArray *matrix = [self buildMatrix:oriStrs.copy];
// 一条完整路径的数组
NSMutableArray *strs = [NSMutableArray array];
for (int i = 0; i < str.length; i++) {
[strs addObject:[str substringWithRange:NSMakeRange(i, 1)]];
}
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
if ([self backetracking:matrix strs:strs marked:marked pathLen:0 r:i c:j]) {
return YES;
}
}
}
return NO;
}
- (bool)backetracking:(NSArray *)matrix strs:(NSArray *)strs marked:(NSArray *)marked pathLen:(int)pathLen r:(int)r c:(int)c {
// 0.即路径长度和字符串长度相等
if (pathLen == strs.count) {
NSLog(@"marked = %@",marked);
return YES;
}
// r < 0 || r >= _rows || c < 0 || c >= _cols || ![oriPathStr isEqualToString:tarPathStr] || marked[r][c]
if (r < 0 || r >= _rows || c < 0 || c >= _cols || matrix[r][c] != strs[pathLen] || [marked[r][c] intValue]) {
// 原路径
return NO;
}
marked[r][c] = @1;
for (NSArray *next in _next) {
int next0 = [(NSNumber *)(next[0]) intValue];
int next1 = [(NSNumber *)(next[1]) intValue];
if ([self backetracking:matrix strs:strs marked:marked pathLen:pathLen + 1 r:(r + next0) c:(c + next1)]) {
return YES;
}
}
marked[r][c] = @0;
return NO;
}
/**
构造一个矩阵 array-完整路径的数组,即a,b,t,g,c...h,并且是一个 rows * cols 的矩阵
a b t g
c f c s
j d e h
*/
- (NSMutableArray *)buildMatrix:(NSArray *)array {
// 0.判断是否有值
if (_rows == 0 || _cols == 0) {
return nil;
}
if (array.count < _rows * _cols) {
return nil;
}
// 1.先构造一个二维数组
NSMutableArray *secondArrM = [NSMutableArray array];
for (int i = 0; i < _rows; i++) {
NSMutableArray *firstArrM = [NSMutableArray array];
for (int j = 0; j < _cols; j++) {
[firstArrM addObject:@""];
}
[secondArrM addObject:firstArrM];
}
// 2.依次将值填充进数组中
int idx = 0;
for (int i = 0; i < _rows; i++) {
for (int j = 0; j < _cols; j++) {
secondArrM[i][j] = array[idx++];
}
}
return secondArrM;
}
@end
测试案例代码
// 12.矩阵中的路径
- (void)matrixHasPath {
MatrixHasPath *hasPath = [[MatrixHasPath alloc] init];
NSString *pathStr = @"abtgcfcsjdeh";
NSMutableArray *tagPaths = [NSMutableArray array];
[tagPaths addObject:@"bfce"];
[tagPaths addObject:@"bfceh"];
[tagPaths addObject:@"acfde"];
[tagPaths addObject:@"bcjd"];
[tagPaths addObject:@"abfceh"];
[tagPaths addObject:@"abtch"];
[tagPaths addObject:@"abtsh"];
for (int i = 0; i < tagPaths.count; i++) {
NSString *tagPath = [tagPaths objectAtIndex:i];
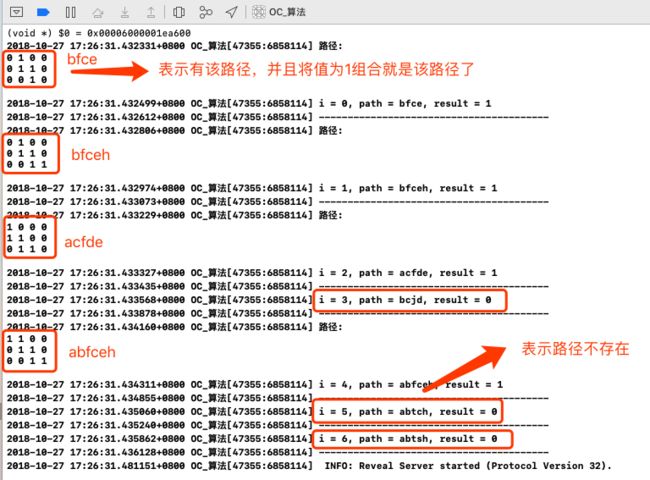
bool result = [hasPath hasPath:pathStr rows:3 cols:4 str:tagPath];
NSLog(@"i = %d, path = %@, result = %d",i,tagPath, result);
NSLog(@"----------------------------------------");
}
}
运行结果
13.机器人的运动范围
题目描述
地上有一个 m 行和 n 列的方格。一个机器人从坐标 (0, 0) 的格子开始移动,每一次只能向左右上下四个方向移动一格,但是不能进入行坐标和列坐标的数位之和大于 k 的格子。
例如,当 k 为 18 时,机器人能够进入方格 (35,37),因为 3+5+3+7=18。但是,它不能进入方格 (35,37),因为 3+5+3+8=19。请问该机器人能够达到多少个格子?
解题思路
参考12题解思路
详细代码如下
- MovingCount_13.h
@interface MovingCount_13 : NSObject
- (int)movintCount:(int)threshold rows:(int)rows cols:(int)cols;
@end
- MovingCount_13.m
@implementation MovingCount_13 {
NSArray *_next;
int _count;
int _rows;
int _cols;
int _threshold; // 行坐标和列坐标的数位之和小于等于于_threshold
NSMutableArray *_digitSum;
}
- (instancetype)init {
self = [super init];
if (self) {
_next = @[@[@0,@(-1)],@[@0,@1],@[@(-1),@0],@[@1,@0]];
}
return self;
}
- (int)movintCount:(int)threshold rows:(int)rows cols:(int)cols {
_rows = rows;
_cols = cols;
_threshold = threshold;
[self initDigitSum];
NSMutableArray *marked = [NSMutableArray array];
for (int i = 0; i < _rows; i++) {
NSMutableArray *firstArrM = [NSMutableArray array];
for (int j = 0; j < _cols; j++) {
[firstArrM addObject:@0];
}
[marked addObject:firstArrM];
}
[self dfs:marked r:0 c:0];
return _count;
}
- (void)dfs:(NSMutableArray *)marked r:(int)r c:(int)c {
if (r < 0 || r >= _rows || c < 0 || c >= _cols || [marked[r][c] intValue]) {
return;
}
marked[r][c] = @1;
if ([_digitSum[r][c] intValue] > _threshold) {
return;
}
_count++;
for (NSArray *next in _next) {
int next0 = [(NSNumber *)(next[0]) intValue];
int next1 = [(NSNumber *)(next[1]) intValue];
[self dfs:marked r:r + next0 c:c + next1];
}
}
- (void)initDigitSum {
int maxNumber = MAX(_rows, _cols);
NSMutableArray *numbers = [NSMutableArray array];
for (int i = 0; i < maxNumber; i++) {
[numbers addObject:@0];
}
for (int i = 0; i < numbers.count; i++) {
int n = i;
while (n > 0) {
numbers[i] = @([numbers[i] intValue] + n % 10);
n /= 10;
}
}
// 初始化原始数组
if (_digitSum == nil) {
_digitSum = [NSMutableArray array];
for (int i = 0; i < _rows; i++) {
NSMutableArray *firstArrM = [NSMutableArray array];
for (int j = 0; j < _cols; j++) {
[firstArrM addObject:@0];
}
[_digitSum addObject:firstArrM];
}
}
// 赋值
for (int i = 0; i < _rows; i++) {
for (int j = 0; j < _cols; j++) {
_digitSum[i][j] = @([numbers[i] intValue] + [numbers[j] intValue]);
}
}
}
@end
测试案例代码
// 13.机器人的运动范围
- (void)movingCount {
MovingCount_13 *movingCount = [[MovingCount_13 alloc] init];
int count = [movingCount movintCount:18 rows:10 cols:10];
NSLog(@"count = %d",count);
}
运行结果
15.二进制中 1 的个数
题目描述
输入一个整数,输出该数二进制表示中 1 的个数。
解题思路
n&(n-1)
该位运算去除 n 的位级表示中最低的那一位。
n : 10110100
n-1 : 10110011
n&(n-1) : 10110000
详细代码如下
/** 输入一个整数,输出该数二进制表示中 1 的个数。*/
+ (int)numberOfOne:(int)number {
int cnt = 0;
while (number != 0) {
cnt++;
number &= (number - 1);
}
return cnt;
}
测试案例代码
// 15.二进制中 1 的个数
- (void)numberOfOne {
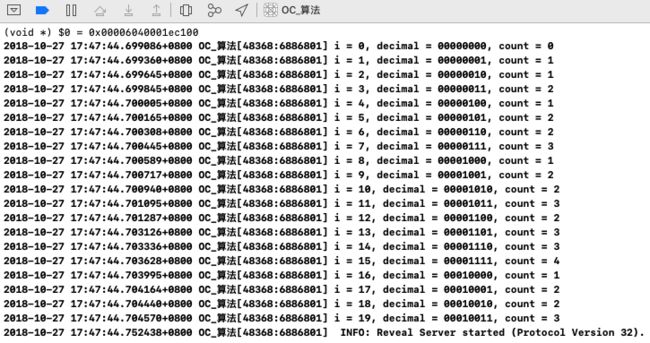
for (int i = 0; i < 20; i++) {
NSLog(@"i = %d, decimal = %@, count = %d",i,[[NSString stringWithFormat:@"%d",i] convertBinarySystemFromDecimalSystem],[NumberOfOne_15 numberOfOne:i]);
}
}
- 十进制数转二进制数 (将其写到NSString 的分类中)
/** 十进制数转二进制数 */
- (NSString *)convertBinarySystemFromDecimalSystem {
NSInteger num = [self intValue];
NSInteger remainder = 0; //余数
NSInteger divisor = 0; //除数
NSString * prepare = @"";
while (true){
remainder = num % 2;
divisor = num / 2;
num = divisor;
prepare = [prepare stringByAppendingFormat:@"%ld",remainder];
if (divisor == 0){
break;
}
}
NSString * result = @"";
for (NSInteger i = prepare.length - 1; i >= 0; i --){
result = [result stringByAppendingFormat:@"%@",[prepare substringWithRange:NSMakeRange(i , 1)]];
}
// 补齐8位显示
while (result.length < 8) {
result = [NSString stringWithFormat:@"0%@",result];
}
return result;
}
运行结果
16.数值的整数次方
题目描述
给定一个 double 类型的浮点数 base 和 int 类型的整数 exponent,求 base 的 exponent 次方。
解题思路
下面的讨论中 x 代表 base,n 代表 exponent。
因为 (x*x)n/2 可以通过递归求解,并且每次递归 n 都减小一半,因此整个算法的时间复杂度为 O(logN)。
详细代码如下
/** 数值的整数次方 */
+ (double)power:(double)base exponent:(int)exponent {
if (exponent == 0) {
return 1;
}
if (exponent == 1) {
return base;
}
bool isNegative = NO;
if (exponent < 0) {
exponent -= exponent;
isNegative = YES;
}
double pow = [self power:base * base exponent:exponent / 2];
if (exponent % 2 != 0) {
pow = pow * base;
}
return isNegative ? 1 / pow : pow;
}
测试案例代码
// 16.数值的整数次方
- (void)power {
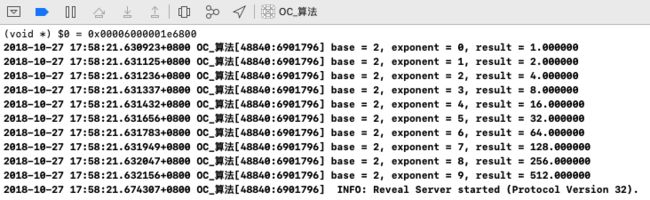
for (int i = 0; i < 10; i++) {
NSLog(@"base = 2, exponent = %d, result = %f",i,[power_16 power:2 exponent:i]);
}
}
运行结果
18.在 O(1) 时间内删除链表节点
- iOS - 节点,链表的实现 - 本题用到该数据类型
题目描述
删除链表节点
解题思路
1.如果该节点不是尾节点,那么可以直接将下一个节点的值赋给该节点,然后令该节点指向下下个节点,再删除下一个节点,时间复杂度为 O(1)。
2.否则,就需要先遍历链表,找到节点的前一个节点,然后让前一个节点指向 null,时间复杂度为 O(N)。
综上,如果进行 N 次操作,那么大约需要操作节点的次数为 N-1+N=2N-1,其中 N-1 表示 N-1 个不是尾节点的每个节点以 O(1) 的时间复杂度操作节点的总次数,N 表示 1 个尾节点以 O(N) 的时间复杂度操作节点的总次数。(2N-1)/N ~ 2,因此该算法的平均时间复杂度为 O(1)。
详细代码如下
/** 删除节点 */
- (void)deleteNode {
NSMutableArray *numbers = [NSMutableArray array];
for (int i = 0; i < 10; i++) {
[numbers addObject:@(i)];
}
LinkedArray *linkArray = [[LinkedArray alloc] initLiknedArrayWithNunbers:numbers];
ListNode *headNode = [linkArray getFirstListNode];
ListNode *lastDelNode = [linkArray getLastListNode];
NSLog(@"---------------原始链表数据---------------");
[headNode printAllListNode];
ListNode *newHeadNode = [self deleteNode:headNode tagDelNode:lastDelNode];
NSLog(@"---------------删除后链表数据---------------");
[newHeadNode printAllListNode];
}
- (ListNode *)deleteNode:(ListNode *)headNode tagDelNode:(ListNode *)tagDelNode {
// 头节点和要删除的节点为空
if (headNode == nil || tagDelNode == nil) {
return nil;
}
if (tagDelNode.next != nil) { // 要删除的节点不是尾节点
ListNode *next = tagDelNode.next;
tagDelNode.content = next.content;
tagDelNode.next = next.next;
} else {
ListNode *cur = headNode;
while (cur.next != tagDelNode) {
cur = cur.next;
}
cur.next = nil;
}
return headNode;
}
测试案例代码
// 18.在 O(1) 时间内删除链表节点
- (void)deleteNode {
DeleteNode_18 *deleteNode = [[DeleteNode_18 alloc] init];
[deleteNode deleteNode];
}
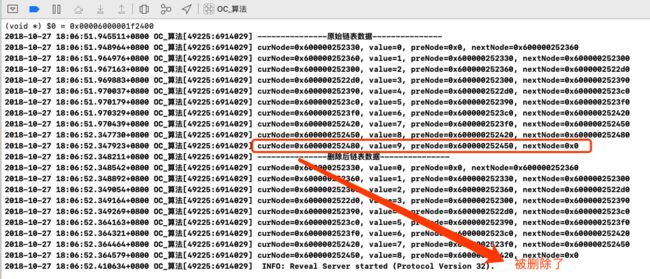
运行结果
18.2 删除链表中重复的结点
题目描述
解题思路
参考18.1的解题思路
详细代码如下
/** 删除 重复节点 */
- (void)deleteDuplicationNode {
NSMutableArray *numbers = [NSMutableArray array];
for (int i = 0; i < 10; i++) {
if (i / 2 == 1) {
[numbers addObject:@(2)];
} else if (i / 3 == 1) {
[numbers addObject:@(3)];
} else {
[numbers addObject:@(i)];
}
}
LinkedArray *linkArray = [[LinkedArray alloc] initLiknedArrayWithNunbers:numbers];
NSLog(@"----------------原始链表数据----------------");
[linkArray printAllListNode];
ListNode *firstNode = [linkArray getFirstListNode];
ListNode *headNode = [self deleteDuplicationListNode:firstNode];
NSLog(@"----------------删除重复节点后的链表数据----------------");
[headNode printAllListNode];
}
// 删除重复节点
- (ListNode *)deleteDuplicationListNode:(ListNode *)pHeadNode {
if (pHeadNode == nil || pHeadNode.next == nil) {
return pHeadNode;
}
ListNode *next = pHeadNode.next;
if (pHeadNode.value == next.value) {
while (next != nil && pHeadNode.value == next.value) {
next = next.next;
}
return [self deleteDuplicationListNode:next];
} else {
pHeadNode.next = [self deleteDuplicationListNode:pHeadNode.next];
return pHeadNode;
}
}
测试案例代码
// 18.2 删除链表中重复的结点
- (void)deleteDuplication {
DeleteNode_18 *deleteNode = [[DeleteNode_18 alloc] init];
[deleteNode deleteDuplicationNode];
}
运行结果
本文参考CS_Nodes 剑指 offer 题解.md 非常感谢该作者
相关知识点文章参考链接地址
- iOS - 节点,链表的实现
- iOS - 栈的实现
- iOS - 二叉树,哈希表的实现
- iOS-算法集锦-剑指offer-百题详解之一
- 更多OC算法详解文章请持续关注作者,本人会在接下来的时间陆续整理。
如有错误,欢迎指正,多多点赞,打赏更佳,您的支持是我写作的动力。
项目连接地址 - ArithmeticDemo