DL知识拾贝（Pytorch）(二)：DL元素之一：激活函数

       我们知道，神经网络实际上就是用于实现复杂的函数，而非线性激活函数能够使神经网络逼近任意复杂的函数。如果没有激活函数引入的非线性，无论神经网络有多少层，输出都是输入的线性组合，与没有隐藏层效果相当，多层神经网络就相当于单层的神经网络，从而对数据只是做仿射变换，⽽多个仿射变换的叠加仍然是⼀个仿射变换，网络的逼近能力就相当有限，这样是不能学习到复杂关系的。
       从定义来讲，只要连续可导的函数都可以作为激活函数，但目前常见的多是分段线性和具有指数形状的非线性函数。下面列出经典的三大激活函数以及一些新的激活函数。

1. 典型激活函数及进阶

1.1 Sigmoid

       sigmoid函数可以将元素的值变换到0和1之间:

       sigmod函数较为符合人的主观认知，将激活的程度控制在不激活（0）到完全激活（1）之间。但确存在几点问题：
       1.从图像可以看到当x趋近于正无穷和负无穷的时候，它的导数都接近0。而BP（后面会讲到的反向传播）是根据梯度来进行的，所以在输出值较大较小时，网络很难更新，即会导致所谓的梯度消失问题。
       2.输出不是以0为中心，而是0.5，所以sigmod函数的输出值恒大于0，这会导致模型训练的收敛速度变慢。
       Pytorch实例：

import torch
import torch.nn.functional as F
from torch.autograd import Variable

import matplotlib.pyplot as plt

x = torch.linspace(-5, 5, 200)   # 构造一段连续的数据
x = Variable(x)      # 转换成张量
x_np = x.data.numpy()    #plt中形式需要numpy形式，tensor形式会报错

y_sigmoid = F.sigmoid(x).data.numpy()    #torch.nn.functional中调用sigmoid函数
plt.plot(x_np, y_sigmoid, c='red', label='sigmoid')
plt.ylim((-0.2, 1.2))
plt.legend(loc='best')  
plt.show()    

1.2 Tanh

       Tanh函数可以将元素的值变换到-1和1之间：

       Tanh函数 的输出均值比 sigmoid 更接近 0，SGD会更接近natural gradient（一种二次优化技术），从而降低所需的迭代次数，主要解决了上面说到的sigmod函数的第二个不足。
       当$x$为非常大或者非常小的时候，由导数推断公式可知，此时导数接近与0，会导致梯度很小，权重更新非常缓慢，从而导致所谓的梯度消失的问题。
       在Pytorch中同样可以直接调用Tanh激活函数，只需要将上面sigmoid示例的函数调用改成Tanh即可：

import torch
import torch.nn.functional as F
from torch.autograd import Variable

import matplotlib.pyplot as plt

x = torch.linspace(-5, 5, 200)   # 构造一段连续的数据
x = Variable(x)      # 转换成张量
x_np = x.data.numpy()    #plt中形式需要numpy形式，tensor形式会报错

y_tanh= F.tanh(x).data.numpy()    #torch.nn.functional中调用tanh函数
plt.plot(x_np, y_tanh, c='red', label='tanh')
plt.grid()
plt.legend(loc='best')  
plt.show()    

1.3 ReLU及其变种

1.3.1 ReLU

       ReLU函数是AlexNet提出的激活函数，很长一段时间是设计CNN网络的默认激活函数。ReLU函数当输入为正数时，输出导数恒为1，缓解了梯度消失的问题。为网络带来稀疏性，当输入值小于0，就会被稀疏掉。

       由于ReLU函数只有线性关系，所以不管是前向传播还是反向传播，都比sigmod和tanh要快很多。
       从图像可以看出，ReLU函数将小于0的全部过滤掉了，虽然它在正区间缓解了梯度消失问题，但却会造成负区间的大量神经元死亡的问题，因为当输入小于零时，导数恒为0，会使很多神经元无法得到更新，也就是负区间的梯度会消失。
       在Pytorch中同样可以直接调用ReLU激活函数，只需要将上面sigmoid示例的函数调用改成ReLU即可：

import torch
import torch.nn.functional as F
from torch.autograd import Variable

import matplotlib.pyplot as plt

x = torch.linspace(-5, 5, 200)   # 构造一段连续的数据
x = Variable(x)      # 转换成张量
x_np = x.data.numpy()    #plt中形式需要numpy形式，tensor形式会报错

y_relu= F.relu(x).data.numpy()    #torch.nn.functional中调用relu函数
plt.plot(x_np, y_relu, c='red', label='ReLU')
plt.grid()
plt.legend(loc='best')  
plt.show() 

1.3.2 Leaky ReLU

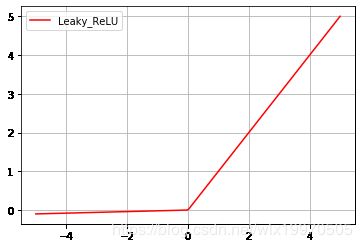
       由于Relu在负区间的神经元死亡问题，于是有了一个变种Leaky Relu，Leaky ReLU给所有负值赋予一个非零斜率，也就是该函数输出对负值输入有很小的坡度。由于导数总是不为零，这能减少静默神经元的出现，允许基于梯度的学习（尽管会很慢）：

       其中$a_i$是（1，+∞）区间内的固定参数。虽然在一定程度上，Leaky ReLU解决了ReLU部分神经元死亡的问题，但在实际使用效果时，实验证明，与ReLU相比，Leaky ReLU对最终的结果几乎没什么影响。
       在Pytorch中同样可以直接调用Leaky ReLU激活函数，只需要将上面sigmoid示例的函数调用改成Leaky ReLU即可,其中，参数negative_slope为负区间斜率值：

import torch
import torch.nn.functional as F
from torch.autograd import Variable

import matplotlib.pyplot as plt

x = torch.linspace(-5, 5, 200)   # 构造一段连续的数据
x = Variable(x)      # 转换成张量
x_np = x.data.numpy()    #plt中形式需要numpy形式，tensor形式会报错

y_LReLU= F.leaky_relu(x,negative_slope=0.02).data.numpy()    #torch.nn.functional中调用leaky_relu函数
plt.plot(x_np, y_LReLU, c='red', label='Leaky_ReLU')
plt.grid()
plt.legend(loc='best')  
plt.show() 

1.3.3 PReLU

       PReLU（Parametric Rectified Linear Unit）来自于何凯明于ICCV2015的paper：论文地址。

       如果$a_i$=0，那么PReLU退化为ReLU；如果$a_i$是一个很小的固定值(如$a_i$=0.01)，则PReLU退化为Leaky ReLU。
       PReLU和 RReLU 以及 Leaky ReLU 有一些共同点，即为负值输入添加了一个线性项。而且这个线性项的斜率$a_i$实际上是在模型训练中学习到的。
       在Pytorch中同样可以直接调用PReLU激活函数，只需要将上面sigmoid示例的函数调用改成PReLU即可，这里的参数weight为训练时得到的参数，这里为了画图方便指定为一个固定的tensor值：

import torch
import torch.nn.functional as F
from torch.autograd import Variable

import matplotlib.pyplot as plt

x = torch.linspace(-5, 5, 200)   # 构造一段连续的数据
x = Variable(x)      # 转换成张量
x_np = x.data.numpy()    #plt中形式需要numpy形式，tensor形式会报错

weight = torch.tensor([0.05])
y_PReLU= F.prelu(x,weight).data.numpy()    #torch.nn.functional中调用PReLU函数
plt.plot(x_np, y_PReLU, c='red', label='PReLU')
plt.grid()
plt.legend(loc='best')  
plt.show() 

1.3.4 RReLU

       RReLU同样属于 Leaky ReLU的变体之一，在RReLU中，负区间的斜率在训练中是随机的，在之后的测试中就变成了固定的了。RReLU在训练环节中，$a_{ji}$ 是从一个均匀的分布$U(I,u)$中随机抽取的数值：

       在Pytorch中同样可以直接调用RReLU激活函数，只需要将上面sigmoid示例的函数调用改成RReLU即可，参数lower和upper为随机分布的下界和上界：

import torch
import torch.nn.functional as F
from torch.autograd import Variable

import matplotlib.pyplot as plt

x = torch.linspace(-5, 5, 200)   # 构造一段连续的数据
x = Variable(x)      # 转换成张量
x_np = x.data.numpy()    #plt中形式需要numpy形式，tensor形式会报错

y_RReLU= F.rrelu(x,lower=1./8, upper=1./3).data.numpy()    #torch.nn.functional中调用RReLU函数
plt.plot(x_np, y_RReLU, c='red', label='RReLU')
plt.grid()
plt.legend(loc='best')  
plt.show() 

       下图为几个ReLU变种的对比：

1.4. ELU及其变种

1.4.1 ELU

       ELU函数是针对ReLU函数的一个改进型。ELU在正区间内的导数处处为1，缓解了梯度消失问题。ELU的输出均值是接近于零的，如果均值非0，就会对下一层造成一个bias，这时候如果激活函数的输出值之间不能相互抵消（即均值非0），就会导致下一层的激活单元有bias shift。当单元很多的时候，bias shift会一直累加，越来越大。相比ReLU，ELU可以取到负值，这让单元激活输出的均值可以更接近0。这比较类似于Batch Normalization的效果但是只需要更低的计算复杂度。虽然LReLU和PReLU都也有负值，但是它们不保证在不激活状态下（就是在输入为负的状态下）对噪声鲁棒。反观ELU在输入取较小值时具有软饱和的特性，提升了对噪声的鲁棒性。

import torch
import torch.nn.functional as F
from torch.autograd import Variable

import matplotlib.pyplot as plt

x = torch.linspace(-5, 5, 200)   # 构造一段连续的数据
x = Variable(x)      # 转换成张量
x_np = x.data.numpy()    #plt中形式需要numpy形式，tensor形式会报错

y_elu= F.elu(x,alpha=1.1).data.numpy()    #torch.nn.functional中调用ELU函数, 需要指定参数alpha
plt.plot(x_np, y_elu, c='red', label='ELU')
plt.grid()
plt.legend(loc='best')  
plt.show()  

1.4.2 SELU

       SELU是NIPS 2017上一篇论文提出来的：论文地址。
       在ELU中，参数alpha是超参数需要提前指定的，而不是根据网络学习而来，这样增加了模型效果对超参调节的依赖，而在SELU中，参数是固定好了的。

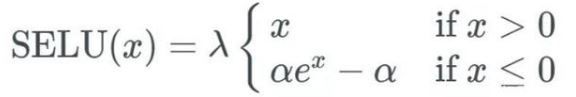
       这篇 NIPS 投稿论文虽然只有 9 页正文，却有着 93 页证明附录，来证明（非训练网络学习到）参数的值为：

       详细推导见论文或者Github。
       那么这样的一个激活函数有什么好处呢？从原论文可以看出，SELU可以实现自归一化。
       先对于BN等外部归一化方式，SELU对神经元激励进行自动地shift 和 rescale，在没有明确的归一化的情况下去实现零均值和单位方差（也就是使得输出数据服从高斯分布）。数据的高斯分布可以使在各层之间传播的张量收敛。这样一来就避免了梯度突然消失或爆炸性增长的问题，从而使学习过程更加稳定。

import torch
import torch.nn.functional as F
from torch.autograd import Variable

import matplotlib.pyplot as plt

x = torch.linspace(-5, 5, 200)   # 构造一段连续的数据
x = Variable(x)      # 转换成张量
x_np = x.data.numpy()    #plt中形式需要numpy形式，tensor形式会报错

y_selu= F.selu(x).data.numpy()    #torch.nn.functional中调用SELU函数
plt.plot(x_np, y_selu, c='red', label='SELU')
plt.grid()
plt.legend(loc='best')  
plt.show()   

1.4.3 GELU

       GELU的论文来自于2016年：论文地址。但直到现在才被关注，在NLP领域的一些Transformer 模型（Google 的 BERT 和 OpenAI 的 GPT-2）中得到了应用。
       先来看一下GELU长什么样？

import torch
import torch.nn.functional as F
from torch.autograd import Variable

import matplotlib.pyplot as plt

x = torch.linspace(-5, 5, 200)   # 构造一段连续的数据
x = Variable(x)      # 转换成张量
x_np = x.data.numpy()    #plt中形式需要numpy形式，tensor形式会报错

y_gelu= F.gelu(x).data.numpy()    #torch.nn.functional中调用GELU函数
plt.plot(x_np, y_gelu, c='red', label='GELU')
plt.grid()
plt.legend(loc='best')  
plt.show()   

       可以看出，当 $x$大于 0 时，输出为 $x$；但 $x$=0 到 $x$=1 的区间除外，这时曲线更偏向于 $y$轴。
       在神经网络的建模过程中，模型很重要的性质就是非线性，同时为了模型泛化能力，需要加入随机正则，例如dropout(随机置一些输出为0,其实也是一种变相的随机非线性激活)， 而随机正则与非线性激活是分开的两个事情， 而其实模型的输入是由非线性激活与随机正则两者共同决定的。
       GELU正是在激活中引入了随机正则的思想，是一种对神经元输入的概率描述，直观上更符合自然的认识，同时实验效果要比ReLU与ELU都要好。
       GELU其实是 dropout、zoneout、Relus的综合，GELUs对于输入乘以一个0,1组成的mask，而该mask的生成则是依概率随机的依赖于输入。假设输入为X, mask为m，则m服从一个伯努利分布( Φ(x), Φ(x)=$P$($X$<=$x$),X服从标准正太分布），这么选择是因为神经元的输入趋向于正太分布，这么设定使得当输入x减小的时候，输入会有一个更高的概率被dropout掉，这样的激活变换就会随机依赖于输入了。
       这里Φ(x) 是正太分布的概率函数，可以简单采用正太分布N(0,1) , 要是觉得不刺激当然可以使用参数化的正太分布N(μ,σ) , 然后通过训练得到μ,σ。论文中提供了近似计算的数学公式，如下：

       论文中也做了不少实验来证明GELU相对于其他激活函数更快更好：

1.5 Swish

       来自于谷歌大脑的paper：Searching for Activation Functions。

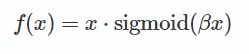
       在代码中的定义也很简单：

def Swish(x ,beta):
    return x * torch.sigmoid(beta * x)

       β是个常数或可训练的参数.Swish 具备无上界有下界、平滑、非单调的特性。

       Swish与ReLU一样有下界而无上界,但是其非单调性确与其他常见的激活函数不同,同时也拥有平滑和一阶导数,二阶导数平滑的特性。
       谷歌的实验证明了Swish在不同的数据集上的表现都要优于很多其他的激活函数，,Swish适应于局部响应归一化,并且在40以上全连接层的效果要远优于其他激活函数,而在40全连接层之内则性能差距不明显。但是根据在mnist数据上AleNet的测试效果却证明，Swish在低全连接层上与Relu的性能差距依旧有较大的优势。
       下图是Google在ImageNet数据集上，不同模型采用激活函数的Acc对比：

1.6 轻量化: ReLU6、h-sigmoid、h-Swish

       ReLU 函数的正区间不施加任何非线性约束，因此当输入很大时会造成梯度爆炸，在部署移动端网络时候是个悲剧，因此，在Mobile V1的时候使用了ReLU6函数。
       ReLU6函数很简单，相当于在ReLU函数的基础上，在正区间6的位置将梯度限制为0，如下：

import torch
import torch.nn.functional as F
from torch.autograd import Variable

import matplotlib.pyplot as plt

x = torch.linspace(-5, 10, 200)   # 构造一段连续的数据
x = Variable(x)      # 转换成张量
x_np = x.data.numpy()    #plt中形式需要numpy形式，tensor形式会报错

y_relu6= F.relu6(x).data.numpy()    #torch.nn.functional中调用RELU6函数
plt.plot(x_np, y_relu6, c='red', label='RELU6')
plt.grid()
plt.legend(loc='best')  
plt.show()   

       h-Swish作为用于轻量化网络的激活函数，出现于谷歌发表的ICCV 2019的MobileNet V3中：论文地址。
       在Swish函数中，由于sigmoid函数的指数计算，特别耗时，不适用于部署在移动端的网络。这里，作者使用ReLU6(x+3)/6来近似替代sigmoid，并命名为h-sigmoid。所以，h-swish定义如下：


       从图像上看，h-swish相当于把Swish硬直化了。下面给出Pytorch实现h-swish的代码：

import torch
import torch.nn as nn
import torch.nn.functional as F


class h_sigmoid(nn.Module):
    def __init__(self, inplace=True):
        super(h_sigmoid, self).__init__()
        self.inplace = inplace

    def forward(self, x):
        return F.relu6(x + 3., inplace=self.inplace) / 6.


class h_swish(nn.Module):
    def __init__(self, inplace=True):
        super(h_swish, self).__init__()
        self.inplace = inplace

    def forward(self, x):
        out = F.relu6(x + 3., self.inplace) / 6.
        return out * x

2. 如何选择激活函数

       关于众多激活函数的选择，还是要看具体的模型和数据以及计算任务来决定，一般而言，首先应该尝试的就是ReLU，事实上，就算是其他激活函数的模型，例如MobileNet V3，在网络中间层依然用的是ReLU函数，只是在末尾或者开头使用h-swish。但由于梯度消失问题，有时要避免使用sigmoid和tanh函数。如果网络学习效果不佳，可能由神经元死亡导致的梯度消失，那么可以尝试ReLU的一些变种激活函数（事实上，ELU及其变种也属于ReLU的变种）。

参考：
[1]. https://www.cnblogs.com/wlzy/p/9688199.html
[2]. https://blog.csdn.net/heifan2014/article/details/79237479
[3]. https://blog.csdn.net/liruihongbob/article/details/86510622
[4]. https://blog.csdn.net/FontThrone/article/details/78636353