算法Java实现 --- 三种静态查找方法
查找的性能分析:
对于查找算法而言,常用“其关键字和给定值进行过比较的记录个数的平均值”作为衡量查找算法的依据。
定义:为了确定记录在查找表中的位置,需要和给定的值进行比较的关键字个数的期望值称为查找算法在查找成功时的平均查找长度。
对于含有n个记录的表。查找成功时的平均查找长度为
ASL=∑i=1nPiCi
其中
Pi
为查找表中第
i
个记录的概率,且
∑i=1nPi=1
Ci
为找到表中关键字与给定值相等的第i个记录时,和给定值已经进行过比较的关键字个数。
静态查找 包括 二分查找、顺序查找、分块查找。
一、二分查找
1、算法思想:又叫折半查找,要求待查找的序列有序。
每次取中间位置的值与待查关键字比较,如果中间位置的值比待查关键字大,则在前半部分循环这个查找的过程,如果中间位置的值比待查关键字小,则在后半部分循环这个查找的过程。直到查找到了为止,否则序列中没有待查的关键字。
【二分查找要求】:1.必须采用顺序存储结构 -- 一般 基于数组
2.必须按关键字大小有序排列。
2、Java实现 ---时间复杂度为 O(logN)
1、非递归实现
public static int biSearch(int []array,int a){
int lo=0;
int hi=array.length-1;
int mid;
while(lo<=hi){
mid=(lo+hi)/2;
if(array[mid]==a){
return mid+1;
}else if(array[mid]2、递归实现
public static int sort(int []array,int a,int lo,int hi){
if(lo<=hi){
int mid=(lo+hi)/2;
if(a==array[mid]){
return mid+1;
}
else if(a>array[mid]){ // 小于中值时在中值前面找
return sort(array,a,mid+1,hi);
}else{ // 大于中值在中值后面找
return sort(array,a,lo,mid-1);
}
}
return -1;
}二、顺序查找法
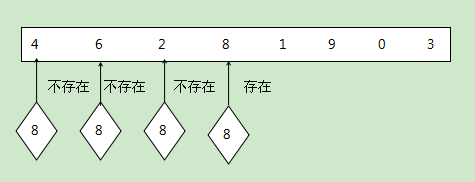
a) 原理:顺序查找就是按顺序从头到尾依次往下查找,找到数据,则提前结束查找,找不到便一直查找下去,直到数据最后一位。
b) 图例说明: 原始数据:int[] a={4,6,2,8,1,9,0,3}; 要查找数字:8
c) Java实现/**顺序查找平均时间复杂度 O(n)
* @param searchKey 要查找的值
* @param array 数组(从这个数组中查找)
* @return 查找结果(数组的下标位置)
*/
public static int orderSearch(int searchKey,int[] array){
if(array==null||array.length<1)
return -1;
for(int i=0;i三、分块查找
分块查找】
分块查找,也称索引顺序查找,是一种折半查找和顺序查找的改进方法。
【思想】
①
把线性表分成若干块,每块包含若干个元素
②块内无序,块间有序。
③
建立一个索引表,把每块中的最大关键字值和每块的第一个元素在表中的位置和最后一个元素在表中的位置存放在索引项中。
④
先确定待查数据元素所在的块,然后再块内顺序查找
如图:
【ASL】
ASLbs=(n/s+s)/2 +1,(其中s是每块的元素个数,n为表长)
【时间复杂度】
时间复杂度为O(n
)~O(log
2
n)
【优缺点】
(1)优点:适用范围大,顺序存储和连式存储都适用;查找效率高
(2)缺点:需要将待查表分块排序,并且要增加一个存储空间用来存储索引表
三大静态查找: 静态查找之顺序查找
静态查找之二分查找
【小结】
Java实现:
/**
* 分块查找
*
* @param index
* 索引表,其中放的是各块的最大值
* @param st
* 顺序表,
* @param key
* 要查找的值
* @param m
* 顺序表中各块的长度相等,为m
* @return
*/
public static int blockSearch(int[] index, int[] st, int key, int m) {
// 在序列st数组中,用分块查找方法查找关键字为key的记录
// 1.在index[ ] 中折半查找,确定要查找的key属于哪个块中
int i = binarySearch(index, key);
if (i >= 0) {
int j = i > 0 ? i * m : i;
int len = (i + 1) * m;
// 在确定的块中用顺序查找方法查找key
for (int k = j; k < len; k++) {
if (key == st[k]) {
System.out.println("查询成功");
return k;
}
}
}
System.out.println("查找失败");
return -1;
} b. 建立一个索引表,把每块中最大的关键字值按块的顺序存放在一个辅助数组中,这个索引表也按升序排列;
c. 查找时先用给定的关键字值在索引表中查找,确定满足条件的数据元素存放在哪个块中,查找方法既可以是折半方法,也可以是顺序查找。
d. 再到相应的块中顺序查找,便可以得到查找的结果。
四、动态查找方法
动态表查找
二叉排序树(二叉查找树):
定义:二叉排序树或者是空树,或者是具有下列性质的一颗树:
-
若他的左子树不为空,则左子树上所有结点的值均小于其根节点的值
-
若他的右子树不为空,则右子树上所有结点的值均大于其根节点的值
-
他的左右子树也均是二叉排序树
关于二叉排序树的Java实现,这篇博文有详细的介绍,可以参考一下
http://blog.csdn.net/evankaka/article/details/48088241
由于二叉排序树的特性,使得我们对其进行中序遍历时就很容易得到一个非递减的有序序列,因此二叉排序树也经常用于排序操作。