AQI(空气质量指数)分析与预测（二）
AQI(空气质量指数)分析与预测（一）
数据分析
哪些城市的空气质量较好/较差
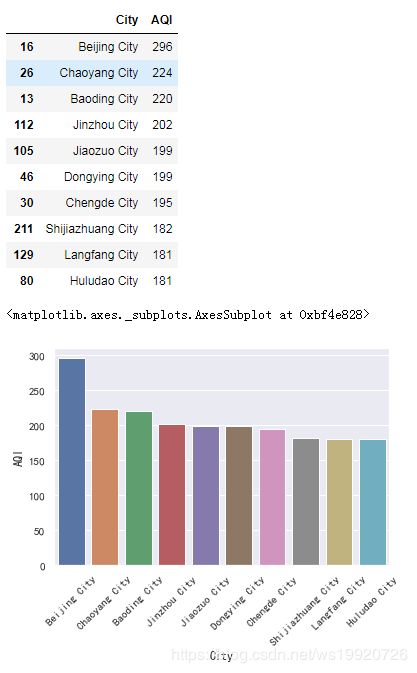
#空气质量最好的几个城市
t = data['Ciyt','AQI'].sort_values('AQI') #根据AQI升序排列
diaplay(t.iloc[:10]) #空气质量最好的十个城市
plt.xticks(rotation=45) #X轴坐标名称倾斜45度
sns.barplot(x='City', y='AQI', data=t.iloc[:10])
#空气质量最差的十个城市
s = data['Ciyt','AQI'].sort_values('AQI',ascending=False) #降序排列
display(s.iloc[:10])
plt.xticks(rotation=45)
sns.barplot(x='City', y='AQI', data=s.iloc[:10])
全国城市的空气质量
城市空气质量等级统计
对于AQI，可以对空气质量进行等级划分，划分标准如下表所示：
| AQI指数 | 等级 | 描述 |
|---|---|---|
| 0-50 | 一级 | 优 |
| 51-100 | 二级 | 良 |
| 101-150 | 三级 | 轻度污染 |
| 151-200 | 四级 | 中度污染 |
| 201-300 | 五级 | 重度污染 |
| >300 | 六级 | 严重污染 |
根据该标准，我们来统计全国空气质量每个等级的数量
#编写函数，将AQI转换为对应的等级
def value_to_level(AQI):
if AQI >= 0 and AQI <= 50:
return '一级'
if AQI >= 51 and AQI <= 100:
return '二级'
if AQI >= 101 and AQI <= 150:
return '三级'
if AQI >= 151 and AQI <= 200:
return '四级'
if AQI >= 201 and AQI <= 300:
return '五级'
else:
return '六级'
level = data['AQI'].apply(value_to_level)
display(level.value_counts())
sns.countplot(x=level, order=['一级','二级','三级','四级','五级','六级'])
可见，我们城市的空气质量主要以一级（优）与二级（良）为主，三级（轻度污染）占一部分，更高污染的城市占少数。
空气质量指数分布
sns.scatterplot(x='Longitude', y='Latitude', hue='AQI', palette=plt.cm.RdYlGn_r, data=data)
从结果我们可以发现，从大致的地理位置上看，西部城市好于东部城市，南部城市好于北部城市。
临海城市是否空气质量优于内陆城市
数量统计
#统计临海城市与内陆城市的数量
display(data['Coastal'].value_counts())
sns.countplot(x='Coastal', data=data)
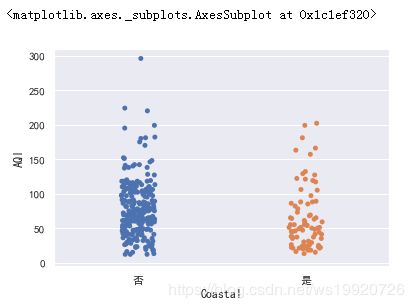
#散点分布
sns.stripplot(x='Coastal', y='AQI', data=data)
sns.swarmplot(x='Coastal', y='AQI', data=data)
#分组计算的空气质量的均值
display(data.groupby('Coastal')['AQI'].mean())
sns.barplot(x='Coastal', y='AQI', data=data)
在柱形图中，仅显示了内陆城市与临海城市空气质量指数（AQI）的均值对比，我们可以使用箱线图来显示更多信息。
sns.boxplot(x='Coastal', y='AQI', data=data)
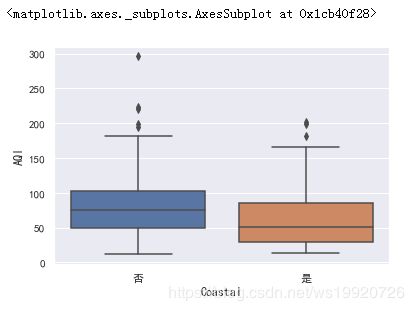
也可以绘制小提琴图，除了能够展示箱线图的信息外，还能呈现出分布的密度。
sns.violinplot(x='Coastal', y='AQI', data=data)
差异检验
我们可以进行两样本t检验，来查看临海城市与内陆城市的均值差异是否显著。
from scipy import stats
coastal = data[data['Coastal']=='是']['AQI']
inland = data[data['Coastal']=='否']['AQI']
#进行方差齐性检验
stats.levene(coastal, inland)
当不确定两总体方差是否相等时，应先利用levene检验，检验两总体是否具有方差齐性。
p值远大于0.05，认为两总体具有方差齐性。
如果两总体不具有方差齐性，需要将equal_val参数设定为“False”。
需注意的情况：
如果两总体具有方差齐性，错将equal_var设为False，p值变大。
两总体方差不等时，若没有将equal_var参数设定为False，则函数会默认equal_var为True，这样会低估p值。
#进行两样本t检验
r = stats.ttest_ind(coastal, inland, equal_var=True) #因为p值远大于0.05，故equal_var设定为‘True’
print(r)
#原假设：沿海城市AQI<=内陆城市AQI
#备择假设：沿海城市AQI>内陆城市AQI
#使用右侧单边检验
p = stats.t.sf(r.statistic, df=len(coastal)+len(inland)-2)
print(p)
通过两样本t检验可知，有超过99%的几率可以认为，沿海城市的空气质量好于内陆城市。