Brian2学习笔记一 Introduction to Brian part1:Neurons
Brian2学习笔记一 Introduction to Brian part 1 :Neurons
- 1. 前言
- 2. 正文
- 2.1 单位系统(Units system)
- 2.2 一个简单的模型(A simple model)
- 2.3 添加脉冲(Adding spikes)
- 2.4 不应期(Refractoriness)
- 2.5 多个神经元(Multiple neurons)
- 2.6 参数系统(Parameters)
- 2.7 随机神经元(Stochastic neurons)
- 2.8 结束教程(End of tutorial)
- 3、学习总结
1. 前言
本文根据Brian2 官方英文教程进行整理总结
Brian2的官方安装教程链接:
链接: https://brian2.readthedocs.io/en/stable/introduction/install.html.
官方文档链接及Jupyter notebook学习资料:
链接: https://brian2.readthedocs.io/en/stable/resources/tutorials/1-intro-to-brian-neurons.html.
推荐几个CSDN上不错的类似教程:
1、链接: https://blog.csdn.net/u013751642/article/details/80918311.
2、链接: https://blog.csdn.net/lemonade_117/article/details/81105303.
3、链接: https://blog.csdn.net/xiaoqu001/article/details/80422546#_Tutorial_84.
最近在学习脉冲神经网络SNN (Spiking Neural Network),Python 的包Brian2 是一个非常实用有效的工具,由于网上资料比较少,并且官方文档为英文原版,所以就对官方的文档进行了一定的翻译和整理,并加入了自己的一些心得,同时附上网上的一些学习资料,非常感谢作者的分享,给我的学习带来了很大的帮助,并且效率也提高了很多。为了自己加深理解,写下这篇博客,鉴于水平有限,所以本文中也许会有一些错误,希望大家能够批评指正。
(本文所有代码运行环境为Anaconda 的 Spyder(python 3.6), 注意运行代码首先要通过如下代码来导入 Brian2的包)
from brian2 import*
2. 正文
2.1 单位系统(Units system)
Brian中有一个使用物理单位的系统。
例如: 20.0 V 20.0 V 20.0V
所有的基本的国际单位制( A , K , s , m , k g , c d , m o l A,K,s,m,kg,cd,mol A,K,s,m,kg,cd,mol)都可以在Brian2中表示,以及这些单位的导出量、标准的单位前缀( m = m i l l i , p = p i c o m=milli, p=pico m=milli,p=pico 等)和一些特殊的缩写( m V ( 毫 伏 ) , p F ( 微 法 ) mV(毫伏),pF(微法) mV(毫伏),pF(微法) 等)也可以在Brian2中表示。
下面列出几个例子:
>>>20*volt
20.0V
>>>1000*amp
1.0kA
>>>1e6*volt
1.0MV
同时还有一些组合单位:
>>>10*nA*5*Mohm
50.0mV
表1 Brian单位系统常用实例
| 单位 | 符号 |
|---|---|
| 伏 | v o l t volt volt |
| 安培 | a m p amp amp |
| 欧姆 | o h m ohm ohm |
| 千克 | k i l o g r a m kilogram kilogram |
| 焦耳 | j o u l e joule joule |
| 秒 | s e c o n d second second |
| 米 | m e t e r meter meter |
| 赫兹 | h e r t z hertz hertz |
| 库伦 | c o u l o m b coulomb coulomb |
| 克 | g r a m gram gram |
| 法拉 | f a r a d farad farad |
数量级还可以用前缀标明 p , n , u , m , k , M , G , T p, n, u, m, k, M, G, T p,n,u,m,k,M,G,T,例如毫伏 m V mV mV 、纳安 n a m p namp namp 、兆欧 M o h m Mohm Mohm ;还其他便利的缩写: c m ( c m e t r e / c m e t e r ) , n S ( n s i e m e n s ) , m s ( m s e c o n d ) , H z ( h e r t z ) , m M ( m m o l a r ) , p F ( p i c o f a r a d ) cm ( cmetre/cmeter), nS (nsiemens), ms (msecond), Hz (hertz), mM (mmolar),pF(picofarad) cm(cmetre/cmeter),nS(nsiemens),ms(msecond),Hz(hertz),mM(mmolar),pF(picofarad) 等等。
通常,在用Brian2 编程的过程中,加上一个物理单位的方法就是用 ∗ * ∗ (乘号)来表示;去除单位的方法就是用 / / / (除号)来表示,是不是很简单呢,接下来附上一段代码:
from brian2 import *
tau = 20*ms
print(tau)
20. ms //输出结果
from brian2 import *
rates = [10, 20, 30]*Hz
print(rates)
[ 10. 20. 30.] Hz //输出结果
from brian2 import *
rates = [10, 20, 30]*Hz
print(rates/Hz)
[ 10. 20. 30.] //输出结果
2.2 一个简单的模型(A simple model)
接下来我们定义一个简单的模型,在Brian2中,所有的神经元模型都是通过微分方程系统来定义的,接下来用一个简单的例子来解释:
from brian2 import *
tau = 10*ms
eqs = '''
dv/dt = (1-v)/tau : 1
'''
在Python中, ′ ′ ′ ''' ′′′ 符号用来开始和结束多行字符。所以上面这个例子中eqs其实只有一行等式 d v / d t = ( 1 − v ) / t a u : 1 dv/dt = (1-v)/tau : 1 dv/dt=(1−v)/tau:1,它是用标准的数学符号来表示的。在等式的最后我们可以看到 : 1 : 1 :1,它表示前面方程式最终运算出来的单位,注意:在Brian中,必须保证方程两边的单位保持一致。
现在让我们使用前面定义的微分方程创建一个神经元:
G=NeuronGroup(1,eqs)
在Brian中,你只能用类 NeuronGroup创建一组神经元。这里面有两个参数,其中第一个参数 1 1 1代表了这组神经元中包含的神经元的个数(在本例中,神经元的个数为 1 1 1),第二个参数 e q s eqs eqs则代表了我们前面定义的微分方程。
接下来我们来观察,如果去掉等式中的变量 t a u tau tau会发生什么。执行如下代码:
from brian2 import *
eqs = '''
dv/dt = 1-v : 1
'''
G = NeuronGroup(1, eqs)
run(100*ms)
输出结果出现如下的错误提示:
原因是:微分方程左右两边单位不一致。左边 d v / d t dv/dt dv/dt 的单位是 1 / s e c o n d 1/second 1/second , 而方程的右边 1 − v 1-v 1−v 是无量纲的。在Brian2中的这种行为非常令人困惑,因为这种方程在数学中很常见。但是,对于带物理维度的变量来说这就是错误的,因为它改变了衡量的单位。如果你用时间单位“秒” 来衡量,同样的方程的表现也会与以毫秒为时间单位来测量的不同。所以在Brian2中,为了避免这种错误的发生,必须保证等式两边单位的一致性。
接下来,我们回到正确的等式来进行计算
start_scope()
tau = 10*ms
eqs = '''
dv/dt = (1-v)/tau : 1
'''
G = NeuronGroup(1, eqs)
run(100*ms)
运行结果如图所示,有一个"INFO"提示信息:没有指定的数值分析方法。这对程序的执行没有什么影响,仅仅是提醒我们选择了哪种数值积分方法,我们可以通过显示指定的方法来避免出现这样一个“INFO”信息。(另外,代码中第一行 start scope()可以忽略,用于清空之前的变量)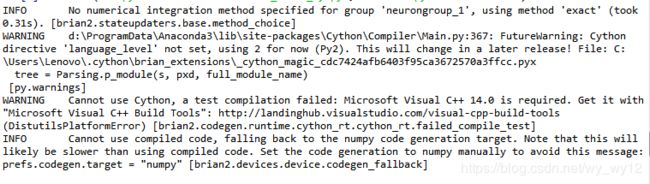
仅仅通过上面这段程序我们没法直观地看出程序执行完后发生了什么了?接下来我们将变量值v在仿真前后的结果打印出来。运行 100 m s 100ms 100ms执行如下代码:
from brian2 import *
start_scope()
tau = 10*ms
eqs = '''
dv/dt = (1-v)/tau : 1
'''
G = NeuronGroup(1, eqs, method='exact')
print('Before v = %s' % G.v[0])
run(100*ms)
print('After v = %s' % G.v[0])
运行结果如下图所示:
![]()
默认情况下,所有的变量初值都为 0 0 0 。但由于等式 d v / d t = ( 1 − v ) / t a u dv/dt=(1-v)/tau dv/dt=(1−v)/tau 的作用,仿真执行一段时间后(本例中为 100 m s 100ms 100ms ),变量 v v v 会趋近于 1 1 1 。程序运行结与我们的预期一致。
现在我们绘制一个图来直观地看变量v是如何随着时间变化的。执行如下代码:
from brian2 import *
start_scope()
tau = 10*ms
eqs = '''
dv/dt = (1-v)/tau : 1
'''
G = NeuronGroup(1, eqs, method='exact')
M = StateMonitor(G, 'v', record=True)
run(30*ms)
plot(M.t/ms, M.v[0])
xlabel('Time (ms)')
ylabel('v')
程序运行结果如下,

这次我们程序只运行了 30 30 30 毫秒,这样我们可以更好地看到v的变化。看起来它的行为和预期的一样,接下来让我们通过在画出预期行为与程序结果的对比图来分析一下。
from brian2 import *
start_scope()
tau = 10*ms
eqs = '''
dv/dt = (1-v)/tau : 1
'''
G = NeuronGroup(1, eqs, method='exact')
M = StateMonitor(G, 'v', record=0)
run(30*ms)
plot(M.t/ms, M.v[0], 'C0', label='Brian')
plot(M.t/ms, 1-exp(-M.t/tau), 'C1--',label='Analytic')
xlabel('Time (ms)')
ylabel('v')
legend()

通过上图,我们发现,预期值(橙色)与仿真值(蓝色)重合。
在这个例子中,使用了StateMonitor对象,它是用来记录仿真运行时神经元变量的值。StateMonitor(G,‘v’,record=True)中有三个参数,第一个参数G表示记录哪一组神经元,第二个参数 v v v 表示想要记录哪个变量,第三个参数指定了记录方式。我们也可以指定 r e c o r d = 0 record=0 record=0,这意味着我们将记录神经元 0 0 0 的所有值。一般情况下,我们必须指定我们想要记录哪一个神经元,因为在大规模仿真中存在很多神经元,如果记录所有神经元的变量值将会消耗大量的RAM。
接下来我们修改一下等式及一些参数看会发生什么变化。执行如下代码:
from brian2 import *
start_scope()
tau = 10*ms
eqs = '''
dv/dt = (sin(2*pi*100*Hz*t)-v)/tau : 1
'''
# Change to Euler method because exact integrator doesn't work here
G = NeuronGroup(1, eqs, method='euler')
M = StateMonitor(G, 'v', record=0)
G.v = 5 # initial value
run(60*ms)
plot(M.t/ms, M.v[0])
xlabel('Time (ms)')
ylabel('v')
2.3 添加脉冲(Adding spikes)
到目前为止,我们仅仅使用微分方程定义了一些简单的神经元模型,接下来让它们可以发放脉冲。执行如下代码:
from brian2 import *
start_scope()
tau = 10*ms
eqs = '''
dv/dt = (1-v)/tau : 1
'''
G = NeuronGroup(1, eqs, threshold='v>0.8', reset='v = 0', method='exact')
M = StateMonitor(G, 'v', record=0)
run(50*ms)
plot(M.t/ms, M.v[0])
xlabel('Time (ms)')
ylabel('v')
程序运行结果如下图。在这个例子中我们为NeuronGroup添加了两个新的关键词: t h r e s h o l d = ′ v > 0. 8 ′ threshold='v>0.8' threshold=′v>0.8′和 r e s e t = ′ v = 0 ′ reset='v = 0' reset=′v=0′,这意味着当 v > 0.8 v>0.8 v>0.8 时将会生成一个脉冲,脉冲过后 v v v 立即复位到 0 0 0 。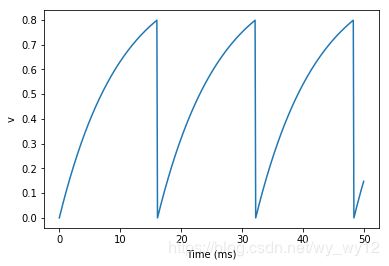
在上图中,v的变化开始时与之前的一样,一直到 t h r e s h o l d v > 0.8 threshold v>0.8 thresholdv>0.8, v v v 迅速回位到 0 0 0,虽然不能直接看到脉冲的生成,但是在Brian2内部已经以脉冲的形式记住了这样一个事件。
接下来我们将在图中直观地将这些脉冲展示出来。执行如下代码:
from brian2 import *
start_scope()
tau = 10*ms
eqs = '''
dv/dt = (1-v)/tau : 1
'''
G = NeuronGroup(1, eqs, threshold='v>0.8', reset='v = 0', method='exact')
statemon = StateMonitor(G, 'v', record=0)
spikemon = SpikeMonitor(G)
run(50*ms)
plot(statemon.t/ms, statemon.v[0])
for t in spikemon.t:
axvline(t/ms, ls='--', c='C1', lw=3)
xlabel('Time (ms)')
ylabel('v')
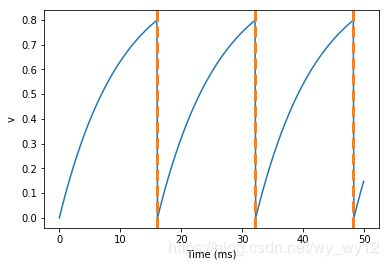
SpikeMonitor对象将你想要记录的脉冲的那组神经元作为它的参数并将脉冲发放时间存储在变量t中。
2.4 不应期(Refractoriness)
神经元模型是的一个最常见的特征就是不应期。也就是神经元在发放一个脉冲之后,它会在一段时间内保持不应期,在这段时间结束之前它都不能再发放另外一个脉冲。接下来我们将展示一下在Brian2中如何实现它,执行如下代码。
from brian2 import *
start_scope()
tau = 10*ms
eqs = '''
dv/dt = (1-v)/tau : 1 (unless refractory)
'''
G = NeuronGroup(1, eqs, threshold='v>0.8', reset='v = 0', refractory=5*ms, method='exact')
statemon = StateMonitor(G, 'v', record=0)
spikemon = SpikeMonitor(G)
run(50*ms)
plot(statemon.t/ms, statemon.v[0])
for t in spikemon.t:
axvline(t/ms, ls='--', c='C1', lw=3)
xlabel('Time (ms)')
ylabel('v')
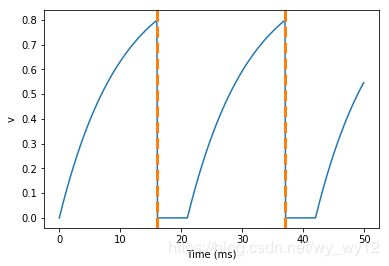
从上面结果图中可以看出,在第一个脉冲之后, v v v 在恢复到正常行为之前持续 5 m s 5ms 5ms 保持为 0 0 0 。为此,我们在代码中需要执行两个操作,首先,在NeuronGroup中添加关键字refractory=5*ms。这样仅仅意味着神经元在这段时间内不能放电,但它不会改变v的行为。为了使 v v v 在不应期内保持常量,在微分方程中v定义的末位添加了(unless refractory)。这意味着微分方程将决定 v v v 的行为除非在不应期这种作用将会失效。
接下来,我们将看一下如果方程中没有添加(unless refractory)将会发生什么?需要注意的是,为了使展示的结果更清楚,我们减小了 t a u tau tau 的值,同时增加了不应期的长度。执行如下代码。
from brian2 import *
start_scope()
tau = 5*ms
eqs = '''
dv/dt = (1-v)/tau : 1
'''
G = NeuronGroup(1, eqs, threshold='v>0.8', reset='v = 0', refractory=15*ms, method='exact')
statemon = StateMonitor(G, 'v', record=0)
spikemon = SpikeMonitor(G)
run(50*ms)
plot(statemon.t/ms, statemon.v[0])
for t in spikemon.t:
axvline(t/ms, ls='--', c='C1', lw=3)
axhline(0.8, ls=':', c='C2', lw=3)
xlabel('Time (ms)')
ylabel('v')
print("Spike times: %s" % spikemon.t[:])
从结果图中可以看出,第一个脉冲的行为和之前是一样的: v v v 在第 8 m s 8ms 8ms 上升到 0.8 0.8 0.8 然后立即复位到 0 0 0 之前发放一个脉冲。由于现在的不应期是 15 m s 15ms 15ms,这意味着神经元将在第 8 + 15 = 23 m s 8+15=23ms 8+15=23ms 的时刻才会继续放电。在第一次放电之后,因为我们这次没有在 d v / d t dv/dt dv/dt 的定义中指定(unless refractory),所以v的值马上就会开始上升。然而,一旦它的值在大约持续8ms之后达到 0.8 0.8 0.8(绿色虚线)甚至超过阈值 v > 0.8 v>0.8 v>0.8,它都不会发放一个脉冲。这是因为在 23 m s 23ms 23ms 时刻之前,神经元一直处在不应期。
2.5 多个神经元(Multiple neurons)
到目前为止,我们只研究了一个神经元,接下为了使用多个神经元做一些有趣的事情,执行如下代码:
from brian2 import *
start_scope()
N = 100
tau = 10*ms
eqs = '''
dv/dt = (2-v)/tau : 1
'''
G = NeuronGroup(N, eqs, threshold='v>1', reset='v=0', method='exact')
G.v = 'rand()'
spikemon = SpikeMonitor(G)
run(50*ms)
plot(spikemon.t/ms, spikemon.i, '.k')
xlabel('Time (ms)')
ylabel('Neuron index')
运行结果: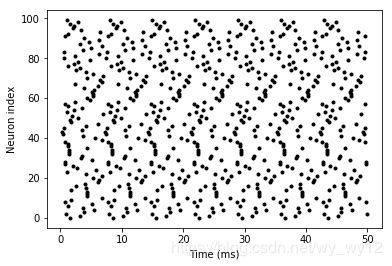
在上述代码中,相较之前有几个变化。首先,我们使用N类代表神经元的个数。其次,用G.v=’rand()’将每个神经元的v指初始化为 0 0 0 到 1 1 1 之间均匀分布的随机值,这样是为了让每一个神经元有一定的差异。当然,最大的差异还是我们的数据展现形式。用变量spikemon.t 代表了对应神经元 i i i 的每个脉冲的发放时间, spikemon.i 代表对应的第 i i i个神经元。在图中用黑点表示,其中x轴表示时间,y轴表示神经元索引。这是神经科学领域中经常使用的标准的“raster plot”。
2.6 参数系统(Parameters)
神经元还能做一些更有趣的事情吗?这部分我们为每个神经元引入一些与微分方程无关的参数,执行如下代码:
from brian2 import *
start_scope()
N = 100
tau = 10*ms
v0_max = 3.
duration = 1000*ms
eqs = '''
dv/dt = (v0-v)/tau : 1 (unless refractory)
v0 : 1
'''
G = NeuronGroup(N, eqs, threshold='v>1', reset='v=0', refractory=5*ms, method='exact')
M = SpikeMonitor(G)
G.v0 = 'i*v0_max/(N-1)'
run(duration)
figure(figsize=(12,4))
subplot(121)
plot(M.t/ms, M.i, '.k')
xlabel('Time (ms)')
ylabel('Neuron index')
subplot(122)
plot(G.v0, M.count/duration)
xlabel('v0')
ylabel('Firing rate (sp/s)')
运行结果:
代码行: v0: 1 为每个神经元声明了一个新的单位为 1 1 1 的神经元参数 v 0 v0 v0 (即无量纲的)。
代码行: G.v0 = ‘i*v0_max/(N-1)’ 为每个神经元初始化了一个从 0 0 0 增加到v0_max(本代码中为3)的v0,其中 i i i代表了每个神经元的索引,也就是第 i i i 个神经元。
所以,在这个例子中,我们以指数方式来驱动神经元的电压值 v 0 v0 v0,但是当 v v v的值逐渐超过 1 1 1时(即 v > 1 v> 1 v>1),它就会触发神经元的放电并重置到回到 0 0 0。其效果就是,它触发峰值的速度将与v0的值相关。对于 v 0 < 1 v0<1 v0<1的神经元,永远无法发放脉冲,但随着 v 0 v0 v0的逐渐增加,它将以一个更高的比率发放脉冲。右图向我们直观的展示了发放率(firing rate)作为 v 0 v0 v0的函数的结果,这是该神经元模型的 I − f I-f I−f曲线。
同时,在这个例子中,大家注意到我们用M.count 来记录变量 SpikeMoniter,它代表一组神经元中每个神经元所发射的脉冲数的数组。用这个除以运行的持续时间(duration)就得到了发放率(firing rate)。
2.7 随机神经元(Stochastic neurons)
通常在神经元模型中会包含一个随机参数来模拟各种形式的神经元噪声。在Brian2中,我们可以在微分方程中引入符号 x i xi xi来做这件事情。严格地说,这个符号是一个“随机微分”但是你可以把它当作是一个均值为 0 0 0,标准差为 1 1 1 的高斯随机变量。我们还应该考虑到单位一致性的问题,所有我们在下面的代码中引入了一个 t a u ∗ ∗ − 0.5 tau**-0.5 tau∗∗−0.5。还有一点需要注意,我们这次使用欧拉法(‘euler’)来改变method的关键字参数;而在前面使用的’exact’方法是不能适用于随机微分方程的。
执行如下代码:
from brian2 import *
start_scope()
N = 100
tau = 10*ms
v0_max = 3.
duration = 1000*ms
sigma = 0.2
eqs = '''
dv/dt = (v0-v)/tau+sigma*xi*tau**-0.5 : 1 (unless refractory)
v0 : 1
'''
G = NeuronGroup(N, eqs, threshold='v>1', reset='v=0', refractory=5*ms, method='euler')
M = SpikeMonitor(G)
G.v0 = 'i*v0_max/(N-1)'
run(duration)
figure(figsize=(12,4))
subplot(121)
plot(M.t/ms, M.i, '.k')
xlabel('Time (ms)')
ylabel('Neuron index')
subplot(122)
plot(G.v0, M.count/duration)
xlabel('v0')
ylabel('Firing rate (sp/s)')
运行结果 这次的运行结果和上一节的结果类似,但是我们加入了噪声。请注意这个曲线的形状是如何改变的:右侧的 I − f I-f I−f 曲线的 firing rate 不再是从 0 0 0 一下子跳跃成一个正值,而是以类似S形的趋势逐渐增加。这是由于无论多么小的驱动力,随机性都可能会导致神经元发放脉冲spike。
这次的运行结果和上一节的结果类似,但是我们加入了噪声。请注意这个曲线的形状是如何改变的:右侧的 I − f I-f I−f 曲线的 firing rate 不再是从 0 0 0 一下子跳跃成一个正值,而是以类似S形的趋势逐渐增加。这是由于无论多么小的驱动力,随机性都可能会导致神经元发放脉冲spike。
2.8 结束教程(End of tutorial)
最后,到了这部分的结束,我们给出最后一个例子,看你是否能明白它是在做什么和为什么。尝试添加一个 StateMonitor 记录其中一个神经元的变量值来帮助你理解这个例子。你也可以在这个例子中尝试一下在本教程中学到的其他内容。一旦你完成了,你就可以进入下一个关于突触的教程了。执行如下代码。
from brian2 import *
start_scope()
N = 1000
tau = 10*ms
vr = -70*mV
vt0 = -50*mV
delta_vt0 = 5*mV
tau_t = 100*ms
sigma = 0.5*(vt0-vr)
v_drive = 2*(vt0-vr)
duration = 100*ms
eqs = '''
dv/dt = (v_drive+vr-v)/tau + sigma*xi*tau**-0.5 : volt
dvt/dt = (vt0-vt)/tau_t : volt
'''
reset = '''
v = vr
vt += delta_vt0
'''
G = NeuronGroup(N, eqs, threshold='v>vt', reset=reset, refractory=5*ms, method='euler')
spikemon = SpikeMonitor(G)
G.v = 'rand()*(vt0-vr)+vr'
G.vt = vt0
run(duration)
_ = hist(spikemon.t/ms, 100, histtype='stepfilled', facecolor='k', weights=ones(len(spikemon))/(N*defaultclock.dt))
xlabel('Time (ms)')
ylabel('Instantaneous firing rate (sp/s)')
3、学习总结
通过这次课程的学习,对Brian2有了一个初步的了解,学习了如何创建神经元的模型,添加脉冲和噪声,同时也对不应期有了初步的认识,本篇文章有参考其他作者的翻译,在文章开头标注了原文的链接,所有的代码程序均在Anaconda 的Spyder (python3.6)中运行成功。如有错误或者问题,欢迎留言指正! 另外,纪念一下,我的第一篇博客!


