《Python机器学习及实践：从零开始通往Kaggle竞赛之路》第2章 基础篇 学习笔记（八）2.1.2.2支持向量机（回归）总结

目录

2.1.2.2支持向量机（回归）

1、模型介绍

2、数据描述

（1）美国波士顿地区房价数据描述

（2）美国波士顿地区房价数据分割

（3）美国波士顿地区房价数据标准化处理

3、编程实践

4、性能测评

5、特点分析

---

2.1.2.2支持向量机（回归）

1、模型介绍

支持向量机（回归）是从训练数据中选取一部分更加有效的支持向量，只是这少部分的训练样本所提供的并不是类别目标，而是具体的预测数值。

2、数据描述

（1）美国波士顿地区房价数据描述

# 代码34：美国波士顿地区房价数据描述
# 从sklearn.datasets导入波士顿房价数据读取器。
from sklearn.datasets import load_boston

# 从读取房价数据存储在变量boston中。
boston = load_boston()
# 输出数据描述。
print(boston.DESCR)

本地输出：

.. _boston_dataset:

Boston house prices dataset
---------------------------

**Data Set Characteristics:**  

    :Number of Instances: 506 

    :Number of Attributes: 13 numeric/categorical predictive. Median Value (attribute 14) is usually the target.

    :Attribute Information (in order):
        - CRIM     per capita crime rate by town
        - ZN       proportion of residential land zoned for lots over 25,000 sq.ft.
        - INDUS    proportion of non-retail business acres per town
        - CHAS     Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
        - NOX      nitric oxides concentration (parts per 10 million)
        - RM       average number of rooms per dwelling
        - AGE      proportion of owner-occupied units built prior to 1940
        - DIS      weighted distances to five Boston employment centres
        - RAD      index of accessibility to radial highways
        - TAX      full-value property-tax rate per $10,000
        - PTRATIO  pupil-teacher ratio by town
        - B        1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
        - LSTAT    % lower status of the population
        - MEDV     Median value of owner-occupied homes in $1000's

    :Missing Attribute Values: None

    :Creator: Harrison, D. and Rubinfeld, D.L.

This is a copy of UCI ML housing dataset.
https://archive.ics.uci.edu/ml/machine-learning-databases/housing/


This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.

The Boston house-price data of Harrison, D. and Rubinfeld, D.L. 'Hedonic
prices and the demand for clean air', J. Environ. Economics & Management,
vol.5, 81-102, 1978.   Used in Belsley, Kuh & Welsch, 'Regression diagnostics
...', Wiley, 1980.   N.B. Various transformations are used in the table on
pages 244-261 of the latter.

The Boston house-price data has been used in many machine learning papers that address regression
problems.   
     
.. topic:: References

   - Belsley, Kuh & Welsch, 'Regression diagnostics: Identifying Influential Data and Sources of Collinearity', Wiley, 1980. 244-261.
   - Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.

结论：总体而言，该数据共有506条美国波士顿地区房价的数据，每条数据包括对指定房屋的13项数值型特征描述和目标房价。另外，数据中没有缺失的属性/特征值，更加方便了后续的分析。

（2）美国波士顿地区房价数据分割

# 代码35：美国波士顿地区房价数据分割
# 从sklearn.model_selection导入数据分割器。
from sklearn.model_selection import train_test_split
# 导入numpy并重命名为np。
import numpy as np

X = boston.data
y = boston.target

# 随机采样25%的数据构建测试样本，其余作为训练样本。
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=33, test_size=0.25)

# 分析回归目标值的差异。
print("The max target value is", np.max(boston.target))
print("The min target value is", np.min(boston.target))
print("The average target value is", np.mean(boston.target))

备注：原来的导入模型from sklearn.cross_validation import train_test_split的时候，提示错误：

from sklearn.cross_validation import train_test_split
ModuleNotFoundError: No module named 'sklearn.cross_validation'

需要替换cross_validation：

from sklearn.model_selection import train_test_split

本地输出：

The max target value is 50.0
The min target value is 5.0
The average target value is 22.532806324110677

结论：预测目标房价之间的差异较大，因此需要对特征以及目标值进行标准化处理。

备注：读者无需质疑将真实房价做标准化处理的做法。事实上，尽管在标准化之后，数据有了很大的变化。但是依然可以使用标准化器中的inverse_transform函数还原真实的结果；并且，对于预测的回归值也可以采用相同的做法进行还原。

（3）美国波士顿地区房价数据标准化处理

# 代码36：训练与测试数据标准化处理
# 从sklearn.preprocessing导入数据标准化模块。
from sklearn.preprocessing import StandardScaler

# 分别初始化对特征和目标值的标准化器。
ss_X = StandardScaler()
ss_y = StandardScaler()

# 分别对训练和测试数据的特征以及目标值进行标准化处理。
X_train = ss_X.fit_transform(X_train)
X_test = ss_X.transform(X_test)
y_train = ss_y.fit_transform(y_train.reshape(-1, 1))
y_test = ss_y.transform(y_test.reshape(-1, 1))

备注：原来的会报错，是因为工具包版本更新造成的；故采用以下方法。

根据错误的提示相应的找出原来出错的两行代码：

y_train = ss_y.fit_transform(y_train)
y_test = ss_y.transform(y_test)

问题出现在上面的两行代码中，例如数据格式为[1, 2, 3, 4]就会出错，如果把这行数据转换成[[1], [2], [3], [4]]就不会出错了。所以要对上面导致出错的两行代码做出修改：

y_train = ss_y.fit_transform(y_train.reshape(-1, 1))
y_test = ss_y.transform(y_test.reshape(-1,1))

3、编程实践

使用分割处理好的训练和测试数据；同时第一次修改模型初始化的默认配置，以展现不同配置下模型性能的差异，也为后面要介绍的内容做个铺垫。

# 代码39：使用三种不同核函数配置的支持向量机回归模型进行训练，并且分别对测试数据做出预测
# 从sklearn.svm中导入支持向量机（回归）模型。
from sklearn.svm import SVR

# 使用线性核函数配置的支持向量机进行回归训练，并且对测试样本进行预测。
linear_svr = SVR(kernel='linear')
linear_svr.fit(X_train, y_train)
linear_svr_y_predict = linear_svr.predict(X_test)

# 使用多项式核函数配置的支持向量机进行回归训练，并且对测试样本进行预测。
poly_svr = SVR(kernel='poly')
poly_svr.fit(X_train, y_train)
poly_svr_y_predict = poly_svr.predict(X_test)

# 使用径向基核函数配置的支持向量机进行回归训练，并且对测试样本进行预测。
rbf_svr = SVR(kernel='rbf')
rbf_svr.fit(X_train, y_train)
rbf_svr_y_predict = rbf_svr.predict(X_test)

4、性能测评

接下来，就不同核函数配置下的支持向量机回归模型在测试集上的回归性能做出评估。

# 代码40：对三种核函数配置下的支持向量机回归模型在相同测试集上进行性能评估
# 使用R-squared、MSE和MAE指标对三种配置的支持向量机（回归）模型在相同测试集上进行性能评估。
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error

print('R-squared value of linear SVR is', linear_svr.score(X_test, y_test))
print('The mean squared error of linear SVR is', mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(linear_svr_y_predict)))
print('The mean absolute error of linear SVR is', mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(linear_svr_y_predict)))

print('R-squared value of Poly SVR is', poly_svr.score(X_test, y_test))
print('The mean squared error of Poly SVR is', mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(poly_svr_y_predict)))
print('The mean absolute error of Poly SVR is', mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(poly_svr_y_predict)))

print('R-squared value of RBF SVR is', rbf_svr.score(X_test, y_test))
print('The mean squared error of RBF SVR is', mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(rbf_svr_y_predict)))
print('The mean absolute error of RBF SVR is', mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(rbf_svr_y_predict)))

本地输出：

R-squared value of linear SVR is 0.650659546421538
The mean squared error of linear SVR is 27.088311013556027
The mean absolute error of linear SVR is 3.4328013877599624
R-squared value of Poly SVR is 0.40365065102550846
The mean squared error of Poly SVR is 46.24170053103929
The mean absolute error of Poly SVR is 3.73840737104651
R-squared value of RBF SVR is 0.7559887416340944
The mean squared error of RBF SVR is 18.92094886153873
The mean absolute error of RBF SVR is 2.6067819999501114

结论：不同配置下的模型在相同测试集上，存在着非常大的性能差异。并且在使用了径向基（Radial basis function）核函数对特征进行非线性映射之后，支持向量机展现了最佳的回归性能。 

5、特点分析

首次展示了不同配置模型在相同数据上所表现的性能差异。特别是该系列模型还可以通过配置不同的核函数来改变模型性能。因此，建议读者在使用时多尝试几种配置，进而获得更好的预测性能。

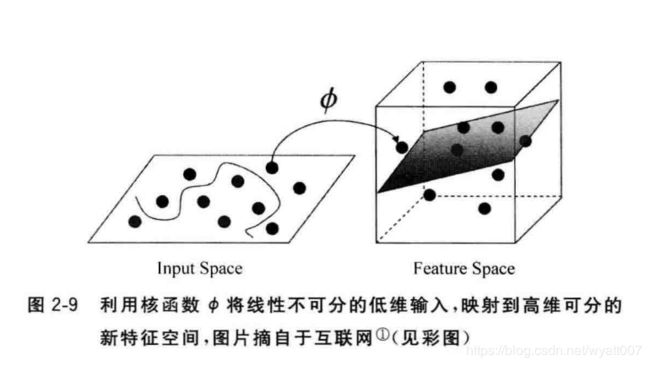
备注：核函数是一项非常有用的特征映射技巧，同时在数学描述上也略为复杂。简单一些理解，便是通过某种函数计算，将原有的特征映射到更高维度的空间，从而尽可能达到新的高维度特征线性可分的程度，如图2-9所示。结合支持向量机的特点，这种高维度线性可分的数据特征恰好可以发挥其模型优势。