斯坦福大学机器学习笔记——多变量的线性回归以及梯度下降法注意事项（内有代码）

在前面博客中介绍了单变量线性回归的实现过程，本文将介绍多变量线性回归算法。
两者的对比如下：
1.数据方面的差异：
单变量线性回归数据：

多变量线性回归数据：

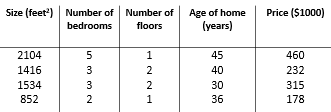
对于单变量线性回归来说，只有一个特征（房子的大小），而对于多变量线性特征回归特征的数量为多个（房子的大小、卧室的数量等）
2.模型构成上的差异：
单变量模型：

多变量模型：

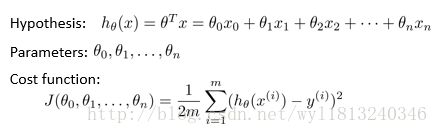
首先介绍多维特征用矩阵形式的表示：
对于上述多变量的数据来说，我们一般使用：
n代表特征的数量；m代表样本的数量；
x(i) 代表第i个训练实例，是特征矩阵中的第i行，是一个向量，例如：
x2=[1416 3 2 40 ]
x(i)j 代表特征矩阵中的第i行第j列，也就是第i个实例中的第j个特征，例如: x(3)4=30
多变量的假设h可以表示为： hθ(x)=θ0+θ1x1+...+θnxn
为了使上面的式子更加简化一些，可以引入 x0=1 ，于是上述公式可以转化为：
hθ(x)=θTx
其中： θ=[θ0;θ1;...;θn] 的列向量， x=[x0;x1;...;xn] 的列向量。
多变量的梯度下降：


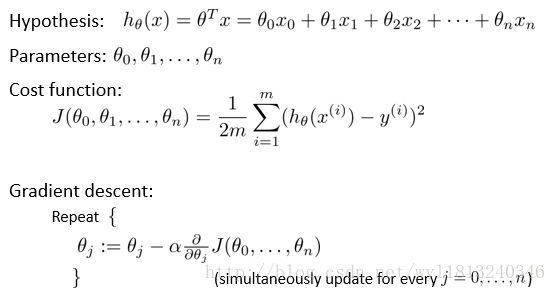
以上就是多变量的梯度下降算法，相对于原来的单变量的线性回归，多变量的线性回归只是参数的数量以及特征的数量增加，其他地方原理基本相同。
多变量梯度下降法的注意事项：

1. 特征缩放
当处理多维特征问题的时候，要保证这些特征具有相近的尺度，这样可以使得梯度下降法收敛的更快。当尺度相差比较大时，如一个特征为身高，单位是米，这该特征的尺度一般为0-2，若另一个特征为体重，单位是斤，则该特征的尺度一般为0-300，所以对于这两个尺度存在较大的差别，在梯度下降算法收敛时会出现下面图形的问题：

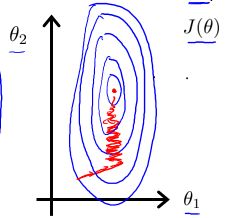
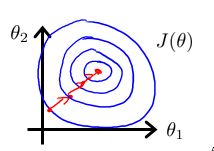
我们知道，梯度下降法是沿着损失函数最大的方向移动步长，所以对于上述图形来说，下降的方向始终沿着垂直的方向移动，会出现图中画出的来回折返最终趋于中心最小值的方向移动。所以迭代次数要求非常多，收敛速度很慢。
如果我们对上述特征的尺度进行归一化，形成的损失的函数等高图如上图中的右图图所示，当沿着损失函数下降最大的方向移动时，即沿着等高线垂直的方向移动，使得收敛的速度很快。
要想完成特征尺度相差不大的要求，要对特征进行缩放，特征缩放的方法有以下几种：
a.对于每个特征求出最大值，然后将每个样本中的该特征除以该特征的最大值。使用公式可以表示为：
xi=ximax(xi)
对于上面的例子来说，若对于一个数据集，身高这个特征的最大值为1.98，体重的这个特征的最大值为256，这对于该数据集中的所有样本的身高特征都除以1.98，对于体重这个特征都除以256，则就完成了特征的缩放。
b.另外一种特征缩放的方式为，对于每一个特征，求出该特征的平均值，然后用该特征的取值减去均值（去均值化），最后用去均值化的结果除以该特征的最大值，使用公式可以表示为：
xi=xi−μimax(xi)
其中， μi 为该特征的均值。
c.实现特征缩放最简单的方法为：
xi=xi−μisn
其中， μi 为该特征的均值， sn 为标准差。
对尺度缩放之后的特征取值范围最大为-3~3，最小为-1/3~1/3，这是两个范围的临界值。
2. 学习率的设置
梯度下降法收敛需要的迭代次数根据模型的不同而不同，我们可以根据绘制损失函数曲线可以得到大致的收敛迭代次数。也可以使用一些自动的测试方法判断是否达到收敛，比如将代价函数与某个阈值进行比较，当代价函数小于该阈值时，则判断为收敛，但是该方法的难点在于选择一个合适的阈值是相当困难的。所以通常使用损失函数曲线，因为它不仅可以判断收敛的迭代次数，同时能够判断梯度下降算法是否正常工作（见下方）。
梯度下降算法的迭代次数同时受到学习率的影响，当学习率设置过小时，迭代的次数会增加；当学习率设置过大时，梯度下降法可能不会收敛，具体的分析可以看http://blog.csdn.net/wyl1813240346/article/details/78366390，下面根据损失函数曲线看学习率的影响：

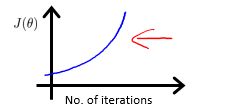
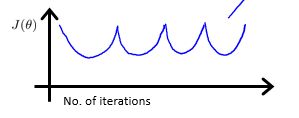
出现上述样式的损失函数的曲线都是由于学习率设置过大引起的，应该使用较小的学习率的值。
在设置学习率时，可以尝试以下学习率：0.01，0.03，0.1，0.3，1，3，10以此方式递增。

多变量线性回归的代码如下：

clear;
close all;

%% 数据处理和初始化

data = load('ex1data2.txt'); % ex1data.txt中第一列是特征，第二列是标签
feature = data(:,1:end-1);    % 取出特征数据

max_feature = max(feature); % 每个特征的最大值
mean_feature = mean(feature);   % 每个特征的均值
std_feature = std(feature); % 每个特征的标准差

% 实现特征归一化
feature = feature_normalized(feature, max_feature, mean_feature, std_feature);

result = data(:,end);  % 出标签数据

% 绘制数据分布，以确定使用哪种假设
% figure;
% plot3(feature(:,1),feature(:,2),result,'bo','MarkerSize', 3);   

[num_sample, num_feature] = size(feature);
feature = [ones(num_sample,1) feature];  % 将特征进行扩展，在原来的基础上增加一列全为1的矩阵

% 初始化
theta = zeros(num_feature+1,1); % 对theta进行初始化
iteration = 8000;  % 设置迭代次数
alpha = 0.01;    % 学习率

%% 训练模型和测试数据

% 训练模型，得到最优的theta值
[theta, all_theta, cost] = gradient_descent(theta, feature, result, iteration, alpha);

% 绘制随着迭代次数增加，损失函数的变化过程
x = 1:iteration;
y = cost;
figure;
plot(x',y);

% 测试数据
test_data = [1520 4;5551 3];   %测试数据
test_data = feature_normalized(test_data, max_feature, mean_feature, std_feature);
[num_test_sample, num_test_feature] = size(test_data);  %测试数据的个数  
test_data = [ones(num_test_sample,1) test_data];  %测试数据的扩充
test_result = test_data * theta;    %测试数据的预测结果

上述代码用到三个函数，分别为：
1.进行特征放缩：

function [normalized_feature, max_feature, mean_feature, std_feature] = feature_normalized(original_feature, max_feature, mean_feature, std_feature)

[num_sample,num_feature] = size(original_feature);
normalized_feature = zeros(num_sample, num_feature);

for i=1:num_feature
%     % 方式1
%     normalized_feature(:,i) = original_feature(:,i)/max_feature(i);
%     % 方式2
%     normalized_feature(:,i) = (original_feature(:,i)-mean_feature(i))/max_feature(i);
    % 方式3
    normalized_feature(:,i) = (original_feature(:,i)-mean_feature(i))/std_feature(i);
end

2.计算损失函数：

function cost = compute_cost(feature, result, theta)

m = length(result); %样本的个数
cost = sum((feature*theta - result).^2)/(2*m);  %计算当前theta下的损失

end

3.实现梯度下降算法：

function [theta, all_theta, cost] = gradient_descent(theta,feature,result,iteration,alpha)

[m,n] = size(feature);  % m代表样本的个数，m代表所需要参数的个数
cost = zeros(iteration,1); % 存储每次迭代的损失函数的值
all_theta = zeros(n, iteration);    % 存储所有theta值

for i=1:iteration

    cost(i) = compute_cost(feature, result, theta); % 计算损失函数
%     cost(i) = sum((feature*theta - result).^2)/(2*m);

    for j=1:n
        theta(j) = theta(j) - alpha * sum((feature * theta - result) .*feature(:,j)) / m;
    end
%     theta(1) = theta(1) - alpha * sum((feature * theta - result) .*feature(:,1)) / m;   % 更新theta1
%     theta(2) = theta(2) - alpha * sum((feature * theta - result) .* feature(:,2)) / m;  % 更新theta2
%     theta(3) = theta(3) - alpha * sum((feature * theta - result) .* feature(:,3)) / m;  % 更新hteta3
    all_theta(:,i) = theta; % 将theta存储起来

end

可以对照http://blog.csdn.net/wyl1813240346/article/details/78366390中的内容，进行单变量和多变量的对比。

本人菜鸟一枚，有什么不对的地方欢迎指正。