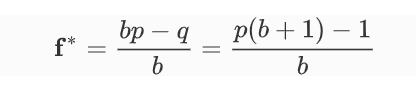凯利公式助你获得更多收益

前不久，在张丹老师博客看到了一篇凯利公式的文章，感觉很有意思，但一些核心代码，博客上（http://blog.fens.me/finance-kelly/）并没有提供，仔细学习后，用Python实现了那些核心代码，如果需要的话可以在文末点击阅读原文在我的GitHub上进行查看。

凯里公式是这样的：假设有一个游戏赌局，你赢的概率是80%，输的概率是20%，赢时的净收益率是100%，输时的亏损率也是100%。如果赢，你每赌1元，那么赢得1元；如果输，则每赌1元，就会输掉1元。赌局可以进行无限次，每次下的赌注可由你自己任意定。如果你的初始资金是100元，那么怎么样下注，即你每次赌多钱，多少仓位，才能使得长期收益最大？

对于胜率80%，从感觉上应该是很有把握的事情了。那么我们先主观判断一次，用90%的仓位去赌一下，看看结果怎么呢？如果下注10次，按80%胜率，8次胜，2次负。我们来模拟10次，计算一下最后的结果，最终可以获利69.84.

数据表格

    win      dat
0   1  190.000000
1   0   19.000000
2   1   36.100000
3   1   68.590000
4   1  130.321000
5   1  247.609900
6   1  470.458810
7   0   47.045881
8   1   89.387174
9   1  169.835630

资金曲线

 

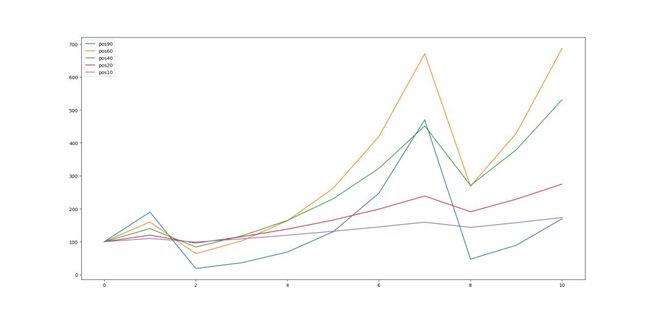
如果我们对仓位进行调整，分别每次下注资金：60%，40%，20%，10%，假设胜率还是80%，模拟10次，我们再看一下结果，10次之后，获利依次是：69.84、587.20、431.28、175.9、73.63。最终获益最高的是最低的8倍多。

-----------------90% 60% 40% 20% 10% 仓位--------------------
        pos90       pos60       pos40       pos20       pos10
0  190.000000  160.000000  140.000000  120.000000  110.000000
1   19.000000   64.000000   84.000000   96.000000   99.000000
2   36.100000  102.400000  117.600000  115.200000  108.900000
3   68.590000  163.840000  164.640000  138.240000  119.790000
4  130.321000  262.144000  230.496000  165.888000  131.769000
5  247.609900  419.430400  322.694400  199.065600  144.945900
6  470.458810  671.088640  451.772160  238.878720  159.440490
7   47.045881  268.435456  271.063296  191.102976  143.496441
8   89.387174  429.496730  379.488614  229.323571  157.846085
9  169.835630  687.194767  531.284060  275.188285  173.630694

资金曲线

可以看出，每次下注60%可以获取收益最大，但波动最大，如果是10%，收益较小，但收益很稳定。

那么问题来了，每次究竟该用多少的仓位去赌博，才能获取最大收益？这就是凯里公式需要解决的问题，具体公式如下：

其中

• f* 投注的比例

• b 赔率，盈亏比，即平均一次盈利与一次亏损两者的比例

• p 胜率

• q 败率，即 1 – p

如果我们把前面的参数代入公式，计算可得f=[0.8*(1+1)-1]/1=0.6

通过凯利公式，我们可以根据胜率，赔率来计算仓位的高低，也可以计算出损失率，从而给出投资者一些指导建议。

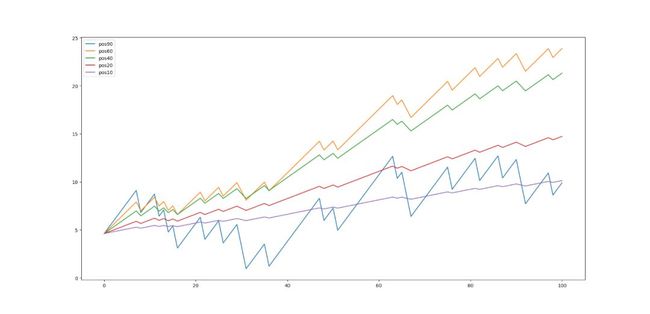
前面的数据只是模拟进行了10次，如果模拟进行100次，那结果则会相差十万八千里。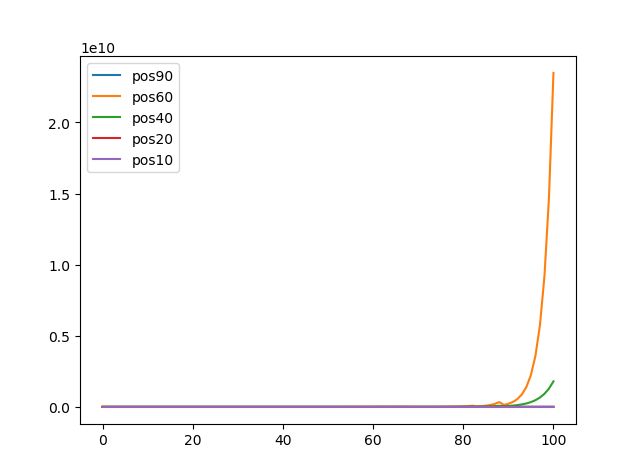

可见，经过100次模拟，他们的收益已经不在同一个数量级。其中仓位60%的收益已经远远超过其他几个，接下来是仓位为40%，其余的仓位收益几乎一样。由于目前数据已经不在一个数量级，我们需要对数据进行对数化处理，来更加直观的展示每一个仓位和收益的变化关系。

对数化处理之后，我们发现仓位为60%时，收益率最高，接下来是40%，仓位10%的最为稳定，仓位20%和10%相对，稳定性较差，但收益稍高。仓位90%的稳定性最差，风险也是最大的。在投资时，如果是保守型怕风险的，则可以选择10%仓位，如果追求高收益，愿意承受更大风险的，则可以选择60%的仓位。

所有源码已上传至GitHub，点击阅读原文即可查看，有什么问题，欢迎留言。

作者：王亨
公众号：数据志
原文链接：http://blog.csdn.net/wzgl__wh/

GitHub：https://github.com/hellowangheng/datazhi/tree/master/kelly