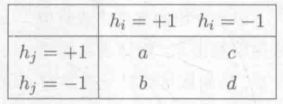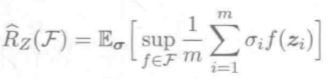机器学习（西瓜书）
一、绪论
1. 假设空间
①假设空间：学习过程可看作一个在所有假设组成的空间中进行搜索的过程，搜索目标是找到能从训练集判断正确的假设
②版本空间：可能存在多个假设（可能互相冲突）与训练集一致，这一假设空间成为版本空间
2. 归纳偏好
任一有效的机器学习算法必有其归纳偏好，偏向选择版本空间中某种假设作为最终模型
没有免费午餐定理NFL：所有问题出现的机会相同或所有问题同等重要时，任何学习算法的期望性能相同
二、模型评估与选择
1. 模型评估方法
以测试集的测试误差作为泛化误差的近似
①留出法：将数据集划分为训练集和测试集（划分时尽量符合随机抽样，一般60%至80%用于训练）
②交叉验证法：将数据集划分为k个相似子集，其中一个作测试集，其余作训练集，最终返回k折平均结果（留一法最准确但计算量大）
③自助法：有放回地自助采样（bootstrap sampling）产生数据集，每个样本在m个样本的m次采样中不被采到的概率趋近于0.368，可未抽中部分作为测试集，抽样结果作为训练集（数据集较小或难以划分训练集时可用，但可能改变原数据分布造成偏差）
2. 性能度量
①均方误差
②错误率/精度
m个样本a个分类错误时，错误率E=a/m，精度accuracy=1-a/m
③查准率/查准率/F1
查准率P=TP/(TP+FP) 查全率R=TP/(TP+FN) BEP（PR曲线平衡点位置）
F1=2×P×R/(P+R)（调和平均）
若多次训练则可计算平均值宏查准率、宏查全率等
④ROC/AUC
真正例率TPR＝TP/(TP+FN)，假正例率FPR=FP/(TN+FP)，调整判断正例的分类阈值，可绘制ROC曲线，ROC曲线下面积为AUC（用于描述预测的排序质量，损失函数相当于描述正例预测值小于或等于反例的情况）
⑤代价敏感错误率/代价曲线
不同类型错误可能造成不同后果，此时计算错误率等指标应用代价而非错误数
错误率E=FN×cost01+FP×cost10
假反例率FNR=1-TPR 代价曲线围成的总面积即为期望总体代价
3. 比较检验
①假设检验
检验单个模型的泛化能力，例如计算出错误率后，再以模型对一个数据集预测时可推算错误率分布，与实际验证的错误率比较，检验置信度。
②交叉验证t检验
比较两个模型的泛化能力。模型A、B经过k折交叉验证得到k个错误率值，可两两配对，进行t检验，原假设为两个模型错误率没有差别
③McNemar检验
比较两个模型，如果两学习器性能相同，则e01=e10，| e01-e10|正态分布，连续性校正后，可构造服从自由度为1的卡方分布的统计量，进行假设检验
④Friedman检验/Nemenyi后续检验
一组数据集多个算法的比较。Friedman检验使用算法比较序值表进行卡方检验，原假设“所有算法性能一样”。拒绝后使用Nemenyi后续检验，若两个算法的平均序值之差超出了临界值域CD，拒绝原假设“两个算法性能相同”。
4. 偏差与方差
偏差-方差分解试图对算法的期望泛化错误率进行拆解，泛化误差可分解为偏差、方差与噪声之和。下式中yD为数据集上标记，y为真实标记，f(x; D)为算法在数据集D上的输出
分别为方差，偏差，噪声
三、线性模型
1. 对数几率回归
对数几率函数 y=11+e-(wTx+b)
，则lny1-y=wTx+b
为几率，反映了x作为正例的相对可能性，函数可用最大似然求参
2. 线性判别分析LDA
给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离。在对新样本进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定新样本的类别
令Xi，μi，Σi分别表示第i类示例的集合、均值向量、协方差矩阵。若将数据投影到直线 ω上，则两类样本的中心在直线上的投影分别为ωTµ0和 ωTμ1 若将所有样本点都投影到直线上，则两类样本的协方差分别为ωTΣ0ω和ωTΣ1ω。
需要让组内方差小，而组间方差大。定义广义瑞利商Sb/Sω，即为最大化目标，其中Sb=(µ0-µ1)(µ0-µ1) T，Sω=Σ0 +Σ1，J=ωTSbωωTSωω
3. 多分类学习器
基本思想是拆分为二分类任务，但有一对一（OvO），一对多（OvR），多对多等形式
多对多—纠错输出码ECOC：a中5个算法分别给4中类别不同的编码并训练，最后测试样本计算之后再与各类别编码计算距离，选距离最小的类作为最终结果
4. 类别不平衡问题
类别不平衡指分类任务中不同类别的训练、样例数目差别很大的情况
欠采样：去除一些反例使得正、反例数目接近，然后再进行学习
过采样：增加一些正例使得正、反例数目接近，然后再进行学习
再缩放（阈值移动）：使用训练集正反样本数对分类器阈值进行调整，以线性分类器为例，原先y/(1-y)>1时预测为正例，再缩放调整为y/(1-y)>m+/m-预测为正例（m+为训练集正例数量）
四、决策树
五、神经网络
1. 神经元模型
2. 感知机与多层网络
感知机由两层神经元组成，可实现与、或、非等线性可分问题，非线性可分问题需要多层功能神经元
3. 反向传播算法BP
算法：
对于输出层单元k，计算误差项：
对于隐含层单元h，计算误差项：
更新每个权值：
其中:
推导：
定义训练样本d的误差Ed：
对每一个样本j，更新一次权重，反复迭代
①单元j是输出层时
②单元j是隐含层时
其中k是输出单元，j为k的上一层
交叉熵损失函数
4. 局部最小问题处理
①多组参数初始化训练后，取损失函数最小的解作为最终参数
②模拟退火以一定概率接受次优解
③随机梯度下降，即计算梯度时加入随机因素
④遗传算法
5. 过拟合问题解决
①损失函数增加正则项
②舍弃机制：每次训练中随机舍弃部分隐层单元
③使用验证集
6. 其他常见神经网络
①RBF径向基函数网络
使用径向基函数作激活函数，输出层为隐层线性组合。有足够多神经元的RBF网络能以任意精度逼近任意函数。常用的高斯径向基函数形如：
②ART竞争型神经网络
无监督，同时具有可塑性（学习新知识的能力）和稳定性（对旧知识的记忆），适于增量学习或在线学习。
由比较层、识别层、识别阔值和重置模块构成。其中，比较层负责接收输入样本，并将其传递给识别层。神经元识别层每个神经元对应一个模式类，神经元数目可在训练过程中动态增长以增加新的模式类。在接收到比较层的输入信号后，识别层神经元之间相互竞争以产生获胜神经元。竞争的最简单方式是，计算输入向量与每个识别层神经元所对应的模式类的代表向量之间的距离，距离最小者胜。获胜神经元将向其他识别层神经元发送信号，抑制其激活。若输入向量与获胜神经元所对应的代表向量之间的相似度大于识别阈值，则当前输入样本将被归为该代表向量所属类别，同时，网络连接权将会更新，使得以后在接收到相似输入样本时该模式类会计算出更大的相似度。否则，重置模块将在识别层增设一个新的神经元，其代表向量就设置为当前输入向量。
③SOM自组织映射网络
一种竞争学习型的无监督神经网络，它能将高维输入数据映射到低维空间，同时保持输入数据在高维空间的拓扑结构，即将高维空间中相似的样本点映射到网络输出层中的邻近神经元。网络在接收输入向量后，将会确定输出层获胜神经元，它决定了该输入向量在低维空间中的位置。SOM的训练目标就是为每个输出层神经元找到合适的权向量，以达到保持拓扑结构的目的。
在接收到一个训练样本后，每个输出层神经元会计算该样本与自身携带的权向量之间的距离，距离最近的神经元成为竞争获胜者、称为最佳匹配单元。然后，最佳匹配单元及其邻近神经元的权向量将被调整，以使得这些极向量与当前输入样本的距离缩小．这个过程不断地代，直至收敛。
④级联相关网络
将网络结构也当作学习目标之一，并希望找到最符合数据特点的网络结构。级联是指建立层次连接的层级结构。在开始训练时，网络只有输入层和输出层，处于最小拓扑结构；随着训练的进行，新的隐层神经元逐渐加入，从而创建起层级结构。当新的隐层神经元加入时，其输入端连接权值是固定的。相关是指通过最大化新神经元的输出与网络误差之间的相关性来训练相关的参数。
⑤Elman网络
一种常见的递归神经网络：允许网络中出现环形结构，让一些神经元的输出反馈回来作为输入信号，即网络在t时刻的输出状态与t-1时刻的网络状态有关，从而能处理与时间有关的动态变化。
⑥Boltzmann机
将每个训练样本视为一个状态向量，使其出现的概率尽可能大。使用CD对比散度算法进行训练
7. 深度学习
典型的深度学习模型就是很深层的神经网络。但多隐层神经网络难以直接用经典算法进行训练，因为误差在多隐层内逆传播时，往往会“发散”而不能收敛到稳定状态。
可用预训练（使用以往类似任务的参数，对本次参数初始化）+微调，或权值共享（如CNN）
六、支持向量机
七、贝叶斯分类器
八、集成学习
1. 集成学习
由一组个体学习器组成，若由同质学习器组成（如全是决策树），则其中的个体称“基学习器”；异质时个体称“组件学习器”。
学习器结合的好处：扩大假设空间（可能有的假设在单学习器不能考虑到），解决多假设达到同等性能的选择，减小陷入局部最优风险
2. Boosting
主要关注降低偏差。先从初始训练集训练出一个基学习器，再对先前基学习器做错的训练样本在后续给予更多关注，训练下一个基学习器，如此重复进行，直至基学习器数目达到事先指定的值T，最终将这T个基学习器进行加权结合。
Adaboost使用各基学习器结果的线性组合作为示性函数，每个分类器权重在迭代中计算
3. Bagging与随机森林
①Bagging(Bootstrap Aggregating)
主要关注降低方差。对m个样本的数据集自助抽样，得到T个有m样本的数据集，各自训练模型后投票或取平均输出结果。每个数据集自己训练时，包外样本（未抽到样本）可做验证集。
②随机森林
随机森林以随机树为基学习器，每个决策树随机从d的属性中选取k个进行训练，一般k=log2d 。随机森林起始性能较差，但最终泛化性能较好。
4. 结合策略
①平均法
简单平均，加权平均（权重可从数据学习而得）
②投票法
绝对多数投票（过半时标记），相对多数投票（得票最多标记），加权投票
③学习法
通过另一个学习器来进行结合。个体学习器称为初级学习器，用于结合的学习器称为次级学习器或元学习器。
Stacking算法使用初级学习器的输出被当作样例输入特征，而初始样本的标记仍被当作样例标记（一般用初级训练器未使用的包外数据训练次级学习器）。
其他算法还有MLR多响应线性回归、BMA贝叶斯模型平均
5. 多样性
①多样性度量
分类器hi，hj的预测结果列联表如下
不合度量：disij=(b+c)/m
相关系数：ρij=ad-bc(a+b)(a+c)(c+d)(b+d)
Q统计量：Qij=ad-bcad+bc
K统计量：K=p1-p21-p2，一致概率p1=a+dm，偶然一致概率p2=a+ba+c+(c+d)(b+d)m2
K误差图：图中每一点是一对分类器，点云位置越高则个体学习器准确性越低，位置越靠右则个体学习器多样性越小
②多样性增强
数据样本扰动：采样法从初始数据集抽样产生样本扰动，对不稳定基学习器有效，如决策树、神经网络等
输入属性扰动：随机子空间算法每次抽取部分属性训练个体学习器，适用于荣誉属性较多情况
输出表示扰动：“翻转法”随机修改一些训练样本标记，“输出调制法”将分类转为回归输出等
算法参数扰动：随机设置不同参数，如神经网络隐层神经元数、初始权值等
九、聚类
1. 性能衡量
①外部指标（将聚类结果与某个参考模型比较）
JC系数 JC=a/(a+b+c)
FM指数 FMI=aa+b·aa+c
Rand指数 RI=2(a+d)m(m-1)
②内部指标
DB指数 DBI=1/ki=1kmaxj≠iavgCi+avgCjdcenμi,μj
Dunn指数 DI=min1≤i≤k{minj≠i(dmin(Ci,Cj)max1≤l≤kdiam(Cl))}
2. 距离计算
dist(·,·)需满足条件：①非负性 ②同一性（i,j相等时dist才能为0） ③对称性 ④直递性（三角不等式，dist(xi
, xj
)≤dist(xi
, xk
)+dist(xk
, xj
)）
※不满足直递性时为非度量距离
有序属性度量距离可用闵可夫斯基距离distmkxi,xj=(u=1n|xiu-xju|p)1/p
无序属性度量距离可用VDM距离VDMpa,b=i=1k|mu,a,imu,a-mu,b,imu,b|p
，mu,a,i 为第i个类在属性u上取值a的个数
3. 原型聚类（假设聚类结构可用原型刻画）
①K-Means 样本集中随机抽取k个样本作为初始均值，每个样本纳入距离最近的均值所属的类，再计算新均值向量，如此循环直至均值不变。
②学习向量量化LVQ 假设样本已有标签，初始化一组原型向量
，一个或多个原型向量代表一个类，对所有样本依次计算最近的原型向量，以学习率η进行学习。若样本与最近向量标签相同，则p’=pi＋η(xj-pi)
，否则p’=pi-η(xj-pi)
，循环至满足停止条件。
③高斯混合聚类 记多元高斯分布概率密度函数为p(x|μ,Σ)
，定义高斯混合分布px=i=1kαipxμi,Σi，i=1kαi=1
，可用EM算法求解。首先初始化高斯混合模型参数，计算各xi
由各个高斯混合成分生成的后验概率作为权重，再更新均值向量、协方差矩阵、混合系数，循环直至满足停止条件，之后对xi
标注类标签。
4. 密度聚类（假设聚类结构可由样本分布的紧密程度确定）
DBSCAN算法基于邻域标准ε（距离小于ε即属于邻域），定义某样本xi
邻域内样本数大
于阈值时为核心对象。核心对象xi
邻域内的样本均由xi
密度直达，存在样本序列xi, xk,…,xj
且依次密度直达（如xk
可由xi 密度直达）时称xj
由xi
密度可达，若存在xk
密度可达xi 与xj
，则xi
与xj
密度相连。由样本导出的最大密度相连样本集为类。
算法先找出所有核心对象，对所有核心对象进行遍历地找寻密度可达样本，形成类。
5. 层次聚类（在不同层次对数据划分，形成树形结构）
AGNES算法每次找出两个最近的类进行合并，直至达到预设的类个数。
十、降维与度量学习
1. k近邻学习KNN
给定测试样本后，找出距离最近的k个样本，使用投票法/平均法计算预测结果
2. 低维嵌入
多维缩放MDS要求原始空间中样本间距离在低维空间能够保持，即距离矩阵大致相同。令原始d维空间内m个样本距离矩阵D∈Rm×m，令降维后内积矩阵B=ZTZ，Z∈Rd’×m，d’≤d。以distij表示D中样本i，j的距离，有
，可计算矩阵B，得到Z=WTX，Z为m个样本在新空间的坐标表达。
3. 主成分分析PCA
样本集D，首先进行中心化，再计算协方差矩阵XXT，对其特征值分解，取最大的d’个特征值所对应的特征向量构成投影矩阵
4. 核化线性降维
非线性降维时，可引入核函数K，将样本经过核矩阵映射到高维空间，再进行线性降维
5. 流形学习（借鉴拓扑流形概念降维）
①等度量映射Isomap（重在保住近邻样本间距离）
高维空间中可能直线距离不可达（如需要沿曲面运动等），认为流形在局部上与欧式空间相似，故可对每个点基于欧式距离找近邻点，建立近邻连接图。任意两点间的距离即为近邻连接图上两点之间路径最短问题。进一步使用Dijkstra或Floyd算法得到任意两点间距离后，可再用MDS获得样本在低维空间的坐标。
②局部线性嵌入LLE（重在保住邻域样本间线性关系）
样本点xi
可由k近邻样本表示，如xi=ωijxj+ωikxk+ωilxl
，从样本可以计算出系数矩阵W，(W)ij=ωij，
，M特征值分解后取最小d’个特征值对应的特征向量得到Z，即为样本在低维空间投影。
6. 度量学习
对于两个d维样本，其距离和加权距离可表示如下：
W为对角矩阵，但考虑维度间有相关，可替换成度量矩阵M，度量学习的目标是学习合适的M，具体的学习与场景有关，如分类问题中需要让同类样本距离尽可能小。
十一、特征选择与稀疏学习
1. 特征选择
原因：解决维数灾难问题，且去除不相关特征可降低学习难度（但不能丢失重要特征，对于冗余特征，若正好为中间概念（如目标为体积，冗余特征为底面积）可以保留）
方法：子集搜索+子集评价
2. 过滤式选择
先对数据集进行特征选择，再训练学习器，特征的选择与后续过程无关。
Relief方法使用相关性度量筛选特征。对样本Xi，定义同类样本的最近邻为Xi,nh，异类样本中最近邻为Xi,nm，对属性j，相关统计量为δj=i(diffxij,xi,nmj2-diffxij,xi,nhj2)
（多分类时可对每个异类找最近邻，在第一项使用样本数进行加权平均），相关统计量超过阈值τ时则保留
3. 包裹式选择
将最终学习器性能作为特征子集的评价标准，为给定学习器选择最有利于性能的特征子集。
LVW算法每次随机产生一个特征子集，通过交叉验证估计学习器的误差，在随机试验次数达到停止条件时确定最终特征子集
4. 嵌入式选择
将特征选择和学习器训练过程融为一体，两者在同一个优化中进行。
如岭回归向回归的损失函数中加入正则项，minωi=1m(yi-ωTxi)2+λ|ω|2
，在训练过程中同时筛选特征
5. 稀疏表示与字典学习
样本具有稀疏表达形式时，筛选特征后学习任务可以简化、模型复杂度降低、可解释性更强等好处，类似文本词向量，若有一个字典则可以将稠密数据进行稀疏表示。对数据集{x1,x2,…,xm}，字典学习minB,αii=1m||xi-Bαi||22+λi=1m|α|1
，其中B为字典，αi∈Rk
为xi
的稀疏表示，可以通过调整k来控制稀疏程度。
十二、计算学习理论
1. 基础知识
计算学习理论分析学习任务的困难本质，为算法提供理论保证
2. PAC概率近似正确学习
对任意x，有c(x)=y正确，则称c为目标概念（本质是X到Y映射），目标概念集合为概念类C，即学习的目标。学习算法L有假设空间H，若c∈H则算法L可分（能将所有示例完全正确地区分）。算法的目标是使输出映射h尽可能接近c，以较大概率学得误差满足预设上限的模型。
PAC辨识：算法L以较大概率（1-δ）学得c的近似（误差不超过ε）
PAC可学习：若从分布D独立同分布抽取m个样本，若存在算法L与多项式函数poly()使得对任意m≥poly(1/ε,1/δ,size(x),size(c))，L能从假设空间H中PAC辨识C，则C对H是PAC可学习的。
PAC学习算法：若算法L使C为PAC可学习的，且L运行时间为多项式，则L为C的PAC学习算法。
样本复杂度：满足PAC学习算法所需的最小m为样本复杂度。
3. 有限假设空间（|H|有限）
①可分情形c∈H：则H都是PAC可学习的，需要样例数m≥1/ε(ln|H|+ln1/δ)，h的泛化误差可随样例数目增加以O(1/m)收敛到0
②不可分情形c∉H：以H中泛化误差最小的假设为目标进行学习，类似于PAC可学习，将误差限制改为与最小泛化误差的差值不超过ε，可定义不可知PAC学习。
4. VC维（|H|无限）
增长函数H(m)
：假设空间H对m个示例所能赋予标记的最大可能结果数（如二分类问题两个示例表示可能为4种）
H中的假设对D中示例赋予标记的每种可能结果称为对D的一种“对分”，H能实现D上所有对分，即H(m)=2m 时，称D可被H“打散”
VC维：能被H打散的最大示例集的大小，可表示模型复杂程度
对于VC维为d的假设空间H，其泛化误差上界ε=8dln2emd+8ln4δm
，只与数据量和模型复杂程度有关。任何VC维有限的假设空间H都是不可知PAC可学习的。
5. Rademacher复杂度
VC维算出的泛化误差上界经过了多次放大，Rademacher复杂度在考虑数据分布的情况下计算。
泛化误差上界ε=2dlnemdm+ln1δ2m
6. 稳定性
表示算法在输入变化时输出是否会发生较大的变化
算法β-均匀稳定性：
其中D\i 表示将第i个样例移除后，l表示损失函数（描述标签预测与真实情况差别）
十三、半监督学习
1. 主动学习与半监督学习
①主动学习：在有标签样本基础上，每次选取对模型改良最大的样本询问专家（如SVM找出距离超平面最近的样本）进行标记，从而在少量标记样本的基础上训练出较强的模型
②纯半监督学习：假定未标记样本并非待测数据
③直推学习：假定为标记样本即为待测数据（泛化目标仅在未标记样本中）
2. 生成式方法
假设所有数据都由同一个潜在模型生成（如高斯混合），使用样本训练模型获得未知参数 （需要领域知识，才能预先假设模型）
3. 半监督SVM（S3VM）
S3VM试图找到能分隔有标记样本，并且穿过数据低密度区的划分超平面，TSVM为其中一种
TSVM：先用有标记样本学得SVM，用其对未标记样本打伪标签，求解新的超平面和松弛向量（未标记样本的权重低于有标记）。之后选出两个标签不同且很可能出错的样本交换标签，重新求超平面和松弛向量，再找出两个样本以此迭代同时逐渐增加未标记样本的权重直到与有标记样本相同
4. 图半监督学习
将数据集映射到图，图的结点为样本，边为结点间相似度（可用x计算二范式等）。有标记与无标记的样本共同组成亲和矩阵W，Wij表示第i样本与第j样本的相似度。
迭代式标签传播算法针对多分类问题，使预测结果在有标记样本上尽可能相同，且相似样本有相似标记：
5. 基于分歧的方法
协同训练针对多视图数据，使用多学习器进行训练。假设不同视图具有相容性（关于输出的y 的信息是一致的）、充分（包含可产生最优学习器的信息）、条件独立（给定类别标记条件下独立），则可以对每个视图分别训练分类器，然后将每个分类器的“伪标签”供给其他训练器作为新增有标记样本训练更新，迭代至各学习器不再变化或达到预设轮数
※不只是多视图数据，只要各学习器间差异较大，都能通过协同训练提高泛化性能
6. 半监督聚类
聚类中监督信息包括必连（两个样本必属同一类）与勿连（两个样本必不属同一类），或部分直接有标记的样本
约束K均值算法利用必连与勿连信息，在K均值算法的基础上保证必连和勿连关系。
约束种子K均值利用少量有标记样本，直接作为种子初始化聚类中心，并保证在迭代中不改变有标记样本的类别。
十四、概率图模型
1. 概述
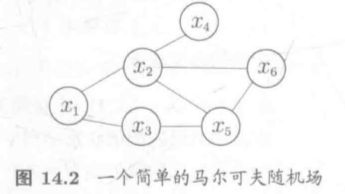
概率图模型使用图表示变量相关关系，结点表示变量，边表示变量间相关关系。根据边不同可分为两种：有向无环图表达变量间依赖关系，称贝叶斯网；无向图表示相关关系，称马尔可夫网。
概率图模型演进：
https://www.zhihu.com/question/53458773/answer/554436625
2. 隐马尔可夫模型HMM（属贝叶斯网生成式模型）
马尔可夫链：yi为有N种取值的状态变量（隐变量），xi为有M种取值的观测变量，i为时刻。在任意时间，观测变量只依赖于状态变量（yt决定xt），yt取决于yt-1（满足条件独立性）。
马尔可夫链的确定需要三组参数λ=[A,B,π]：
①状态转移概率A=[aij]N×N
，aij=P(yt+1=sj|yt=si)
②输出观测概率B=[bij]N×M
，bij=P(xt=oj|yt=si)
③初始状态概率π=(π1,π2,…,πN) ，πi=P(y1=si)
3. 马尔可夫随机场MRF（属马尔可夫网生成式模型）
对于无向图的任一子集，若其中任两结点间都有边连接，则称为团，不被其他团包含的称为极大团。对于n个变量x={x1,x2,…,xn}
，所有团构成集合C，与团Q对应的变量集为XQ，定义联合概率分布Px=1/ZQ∈CφQ(xQ)
，规范化因子Z=xQ∈CφQ(xQ)
，φQ
为势函数，当变量很多时，可以使用极大团C*
替代C，Z一般不需要精确计算只用于保证总概率为1。势函数是定义于XQ的非负实函数，可用于在构造概率分布时调节对不同变量的偏好。
定义若结点集A中的点要到B，都需要经过结点集C，则称A与B被C分离，C称为分离集，在给定C的条件下A与B独立（全局马尔可夫性）。给定某变量的邻接变量时该变量与其他变量独立（局部马尔可夫性），给定其他所有变量时两个非邻接变量独立（成对马尔可夫性）
4. 条件随机场CRF（属马尔可夫网判别式模型）
x={x1,x2,…,xn}
为观测序列，y={y1,y2,…,yn}
为对应标记序列，CRF目标是构建条件概率模型P(y|x)，并假设各变量yv都满足马尔可夫性，即Pyvx,yV{v}=P(yv|x,yn(v))
，其中n(v)为点v的邻域，则（y,x）构成条件随机场。
条件随机场同样使用势函数和团定义P(y|x)，tj(yi+1,yi,x,i)
是转移特征函数，刻画相邻标记变量间相关关系及观测序列对它们的影响；sk(yi,x,i)
为状态特征函数，刻画观测序列x对y的影响；λ与μ为参数。
5. 精确推断方法
①变量消去：利用条件独立性削减目标概率计算量，例如要计算P(x5)时（无向图同样适用）：
或若为无向图时：
②信念传播：将变量消去过程中的求和操作看作一次消息传递，下式看作xi向xj传递了一个消息mij(xj)
信念传播算法先指定一个根节点，所有叶节点向根节点传递消息，知道根节点收到所有邻接节点的消息，再从根节点向叶节点传递消息，直到所有叶节点收到消息。相对于变量消去能够减少冗余计算。
6. 近似推断方法
①MCMC马尔科夫链蒙特卡洛采样
绕过概率分布的推断，直接逼近分布的期望。通过构造马尔可夫链的平稳分布得到后验分布，并从马尔科夫链产生符合后验分布的样本，并基于样本估计。
②变分推断
使用已知的简单分布推断复杂分布，产生一个近似分布
7. 话题模型（属贝叶斯网生成式模型，主要处理离散型数据如文本）
词袋：词是数据基本单元，文档是无顺序地包含一组词的数据对象，话题则表示一个概念（一系列相关的词及其在概念下出现概率）
假定数据集中有K个话题T篇文档，所有词来自于N个词的词典，则以T个N维向量W={ω1，ω2，…，ωT}表示数据集，以K个N维向量βk（k=1,2，…，K）表示话题。ωt,n表示文档t中词n的词频，βk中第n分量表示话题k中词n的词频。
隐狄利克雷分配模型LDA认为每篇文档包含多个话题，用θt∈RK表示文档t中每个话题的比例，分别使用参数为α和η的狄利克雷分布作为主题和词的先验分布。模型中待定参数α、η可使用极大似然进行估计。
十五、规则学习
1. 基本概念
“规则学习”是从训练数据中学习出一组能用于对未见示例进行判别的规则
为规则头（规则结果），箭头右边为规则体（逻辑语言的合取式）
从数据中可以学习出多个规则，每条规则根据一种变量取值判断结果，这些规则可能在某些样本相互冲突，也可以有一些样本未覆盖（可以通过默认规则解决）
命题规则由原子命题和蕴含组成，如“好瓜←(色泽＝青绿)”，一阶规则由原子公式组成，如“：好瓜(X)←根蒂(X，蜷缩)∧脐部(X，凹陷)”（且两个命题长度分别为1和2）
2. 序贯覆盖
即逐条归纳，如Apriori算法，可以自顶向下生成（生成测试法）也可以自下向上生成（数据驱动法）。
3. 剪枝优化
为缓解过拟合需要进行适当剪枝。CN2算法假设规则集结果显著优于样本集后验分布判断结果。REP减错剪枝使用训练集和验证集剪枝至验证集表现最好（通过穷举所有剪枝可能进行后剪枝）。IREP对训练集中产生的每个单条规则分别剪枝（预剪枝）。
4. 一阶规则学习
命题逻辑对事物间关系表达有限，一阶规则容易引入领域知识，且能简洁表达递归关系。一阶规则如：更好(X,Y)←根蒂更蜷(X,Y)∧脐部更凹(X,Y)
FOIL算法采用自顶向下归纳，对于空规则“更好(X,Y)←”先考虑候选文字：
使用FOIL增益选择候选文字，其中m+
为增加候选文字后新规则覆盖正例数，m+
为原规则覆盖正例数，FOIL只考虑正例的信息量（对正例给予更多关注）。在生成一条规则后可以继续增加规则体长度最终生成合适的单条规则加入规则集，生成完成后再对规则集后剪枝。
5. ILP归纳逻辑程序设计
采用自下向上规则生成策略，从一个或多个正例出发逐渐泛化，可通过LGG最小一般泛化结合归结与逆归结来实现。
十六、强化学习
1. 任务与奖赏
MDP马尔可夫决策过程：机器处于环境E中，状态空间X，动作空间A，动作a作用于状态x的转移函数为P，状态转移结果可以对应奖赏函数R。强化学习任务可由四元组E=
2. K-摇臂赌博机
赌博机有K个摇臂，每个摇臂每次以一定概率吐出硬币，赌徒需要一个策略最大化收益
①探索与利用：仅探索方法平均地尝试各个摇臂，将各自吐币概率作为期望的近似估计；仅利用方法每次按下当前最优的摇臂。仅探索法估计较好但失去很多选择最优摇臂的机会，仅利用法没有很好估计期望。
②ε-贪心：以概率ε进行探索，1-ε进行利用。具体ε可以根据分布而定，概率分布较宽时需要更多探索，较集中时则需要更多利用。
③Softmax：基于当前已知的摇臂平均奖赏综合探索和利用，使用Boltzmann分布，下式中τ>0称为温度，Q(i)记录当前摇臂平均奖赏，τ越小则越倾向于利用。
3. 有模型学习
假设E=
4. 免模型学习
环境中转移概率、奖赏函数、状态等难以得知的时候
①蒙特卡罗强化学习
每个策略相当于赌博机中的一个摇臂，使用ε-贪心算法探索最优策略（同策略方法）；或者对一个确定性策略使用ε-贪心算法进行策略评估，从而策略迭代（异策略方法，类似于对抗搜索所用的）
②TD时序差分学习
蒙特卡罗强化学习批处理式地在完成一个采样轨迹（走多步到最后）后对状态-动作对进行奖赏更新，TD则进行增量更新
5. 值函数近似
之前的假设都是有限状态空间，面对无限状态空间时，可以对连续状态空间的值函数进行学习，使用线性函数Vθ(x)＝θTX进行近似，引入核函数可以实现非线性近似。
6. 模仿学习
对人类专家的“状态-动作对”进行模仿
①直接模仿学习
对于人类专家决策轨迹{τ1,τ2,…,τm}，其中τi=
②逆强化学习
从人类范例中反推奖赏函数，假设奖赏函数R(x)=ωTx
