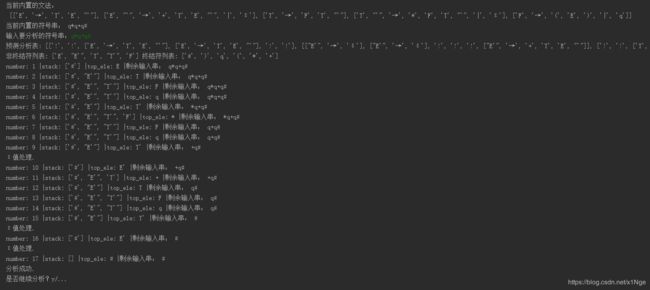
语法分析:自上而下分析(递归下降分析法+预测分析法)
语法分析:自上而下分析
目录
- 语法分析:自上而下分析
- 知识背景
- 递归下降分析法
- 内容一:根据文法生成子程序
- 内容二:调用文法开始符号所对应的子程序
- 预测分析法
- 内容一:构造预测分析表
- 内容二:预测分析法主程序
- 总结
知识背景
百度百科: “语法分析是编译过程的一个逻辑阶段。语法分析的任务是在词法分析的基础上将单词序列组合成各类语法短语,如“程序”,“语句”,“表达式”等等.语法分析程序判断源程序在结构上是否正确.源程序的结构由上下文无关文法描述.语法分析程序可以用YACC等工具自动生成。”
语法分析再编译中也是一个比较很重要的环节,通常情况下语法分析可以分为自上而下分析和自下而上分析。
本文主要介绍自上而下分析(从文法的开始符号出发)的大致框架和细节,并且附上我写的一些代码供大家讨论。首先我看了挺多的关于自上而下的分析,感觉这里一个老师的解释比较清晰,供大家参考 链接。接下来的内容,根据这里老师讲的一个大概框架,写一些我自己的理解,然后分析一下我的代码。
要想进行自上而下分析,我们可以用LL(1)分析法来分析,而这个分析法主要有两种具体实现:递归分析法和预测分析法,有可能其他地方不是这么叫的,但是分析的方法大同小异。
在讨论两种方法前,首先要讨论一下一些预备知识:
Q1:什么是自上而下分析法?自上而下分析的前提是什么?
百度百科: “自上而下分析法是从文法开始符号开始,不断进行推导,直到推导所得的符号串与输入串相同为止。”
简单来解释这句话:
我们有一个既定的文法,和一个需要分析的符号串。接下来我们从文法的开始符号出发,反复地使用文法规定的一些产生式匹配符号串的每一个符号,直到所得的符号串和待分析的符号串相同,则为分析成功,反之匹配不成功。举个例子说明:
G(E):
E→aF
F→b|c
待分析的输入串:ab
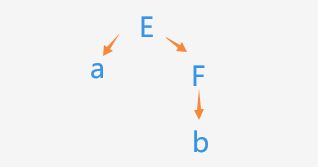
从文法开始符号E出发,E→aF,a匹配成功后,指针指向F,于是找非终结符F的产生式合适的候选式 b匹配,于是匹配成功。
想要对一个文法进行自上而下的分析,要消除文法的二义性,消除左递归,提取左公共因子,计算FIRST集合和FOLLOW集合,判断文法是否为LL(1)型文法,一个文法经过这些步骤,并且是LL(1)文法,则可以用LL(1)分析法的两个具体实现去分析。
Q2:什么是分析过程中的回溯问题?
从上面的例子我们可以看出,在我们碰到非终结符的时候要把非终结符用它对应的产生式的右部来代替,但是一个非终结符往往不止一个候选式(比如上面那个例子的F,F→b|c就有b和c两个选项),这个时候就会出现一个问题,如果我们选择候选式来替代非终结符的时候不能准确判断,这一次的替代是否能够正确推导出匹配的结果,一旦选择的候选式不能推到成功,就要返回上一步,换一个候选式进行推导,这就是“回溯”。例如上面那个例子,我们在拓展F的时候选择了c,会发现匹配失败,然后再返回上一步,选择另一个候选式b,才匹配成功。
Q3:如何解决回溯的问题?
实际上,含有回溯的分析过程并非不可取,只是会浪费很多的资源和时间,因此我们要想办法消除回溯,也就是争取让每一次选择候选式都选择正确的那一个。这就涉及到了下文要讲的FIRST、FOLLOW集合了。
Q4:什么是文法中含有左递归?
左递归分为直接左递归和间接左递归
- 直接左递归
举一个小例子G(E):E→Ea
在这个文法中虽然只有一个产生式,但是对这个产生式进行构造语法树的时候会发现:

这个树会无限向下扩展,无法匹配结束。 - 间接左递归
举一个小例子G(E):

这个文法推导三次后会发现又回到了文法的开始符号又一次出现了,因此又进入循环,无法结束匹配,这就是间接左递归。
Q5:如何解决文法含有左递归的问题?
对于直接左递归,我们通常把它转换成右递归很好理解,举个小例子:
G(E):E→Ea |b
对于这个含有直接左递归的文法,将它转换成右递归的具体做法就是引入一个新的非终结符,通常我们用当前非终结符加’来表示,将文法改为
G(E):
E→E’b
E’ →aE’|ε
可以很容易地证明这两个文法是等价的。
对于间接左递归,通常把非终结符带入来产生直接左递归,例如:
G(E):
![]()
把S右部中的Q用Q的产生式代替,再把Q中的R用R的产生式代替,删除无关产生式后,就能得到一个含有直接左递归的文法:
G(E): S→Sabc|abc|bc|c
然后再将这个产生式按照直接左递归的处理方法进行消除左递归处理。
更一般地,想要让程序自动地消除左递归,具体的做法如下:
1.把文法的所有非终结符进行排序S = [‘A’,‘B’,…]
2.做一个嵌套循环:
其中S[k]为排在S[j]之后的非终结符,bunch_i为非终结符和终结符组成的串
for j in range(len(s)):
for k in range(j):
原产生式中:S[j]→S[k]bunch_1的S[k]用其对应的产生式代替
S[k]→bunch_2|bunch_3|...
推出:S[j]→bunch_2 bunch_1|bunch_3 bunch_1|...
如此,做完循环后该文法若有间接左递归,就将其转换成直接左递归了
消除直接左递归,具体做法见上文
循环结束后删除无用产生式
下面截取一些我写的消除左递归的代码进行讨论,完整源码下载请点击 下载
获取每一条产生式的所有候选式:
temp_split = [] # 将每一个产生式分割以便求的长度来进行分类讨论
# 获取这一条产生式的所有'|'的索引值
temp_or = []
temp_push = []
for q in range(len(lst[j])):
if lst[j][q] == '|':
temp_or.append(q)
# 获取这一条产生式'→'的索引值
temp_get = lst[j].index('→')
# 转换成列表方便组合
temp_push.append(temp_get)
# 合并查找索引列表
temp_search = temp_push + temp_or
# 把一个产生式以'→'和'|'为分隔符分割,将分割后的数据存储在嵌套列表temp_split里
for m in range(len(temp_search)):
if len(temp_search) == 1:
temp_split_1 = [lst[j][temp_search[m] + 1:][:]]
temp_split = temp_split_1[:]
else:
if m == (len(temp_search) - 1):
temp_split.append(lst[j][temp_search[m] + 1:])
else:
temp_split.append(lst[j][temp_search[m] + 1:temp_search[m + 1]])
间接左递归转换成直接左递归:
change = [s[j],"→"]
# change = []
print("ts:",temp_split)
for n in temp_split:
if "'" in n:
n[n.index("'") - 1] += "'"
n.remove("'")
try:
if n[0] == s[k]:
k_push = lst[k][:]
temp_z = []
for z in range(len(k_push)):
if k_push[z] == '|':
temp_z.append(z)
for x in temp_z:
for c in n[1:]:
k_push.insert(x,c)
for c in n[1:]:
if len(c) != 1:
k_push.extend(c)
else:
k_push.append(c)
change.extend(k_push)
change.append("|")
else:
if len(n) == 1:
change.append("".join(n))
else:
change.extend(n)
change.append("|")
except:
print("mark")
lst[j] = change
print("change1:",lst[j])
Q6:什么是提取左公因子?
类似数学上的提取公因式,把形如
E→bunch_1bunch_2|bunch_1bunch_3|…|bunch_1bunch_n|其他开头不是bunch_1的候选式
的产生式改写成 :
E→bunch_1E’|其他开头不是bunch_1的候选式
E’→bunch_2|bunch_3|…|bunch_n
的形式
有话说: 通常情况下,提取左公因子要反复进行,直到所有非终结符的FIRST集合两两不相交。
提取左公因子的代码比较简单,完整代码见 链接
Q7:什么是文法符号的FIRST集,非终结符的FOLLOW集,任意串的FIRST集?
构造这些FIRST集和FOLLOW集的主要目的是为了消除回溯,也就是选择候选式的时候能够更加准确,当然,这些集合在别的地方也有用处。关于Q7,参见我的另外一篇文章:FIRST / FOLLOW集合
Q8:什么是LL(1)型文法?如何判断文法是否为LL(1)型?
若一个文法G为LL(1)文法,则应满足以下条件:
1.文法不含有左递归
2.文法中每一个非终结符产生式中每一个候选式的FIRST集两两不相交(可以反复提取左公因子来接近这个条件)
3.如果文法中的每一个非终结符的FIRST集若含有ε,则每一个候选式的FIRST集和该非终结符的FOLLOW集不相交
下面截取一些我写的判断文法是否为LL(1)文法的代码进行讨论,完整源码下载请点击 下载
下面代码中temp_split为当前产生式的所有候选式的列表,例如E→a|b|c,temp_split = [[‘a’],[‘b’],[‘c’]]
for n in range(len(temp_split) - 1):
for q in range(1,len(temp_split)):
if len(set(get_first_bunch(temp_split[n],temp_lst)) & set(get_first_bunch(temp_split[q],temp_lst))) != 0:
print("error.")
flag = 0
break
for n in range(len(temp_split)):
if 'ε' in get_first_bunch(temp_split[n],temp_lst):
if len(set(get_first_bunch(temp_split[n],temp_lst)) & set(get_follow(temp_lst)["".join(j[:j.index("→")])])) != 0 :
print("error.")
flag = 0
break
Q9:什么是LL(1)分析法?
使用LL(1)分析法的前提见Q1
LL(1)分析法:
假设当前要匹配的输入串符号为a
for i in 每一个候选式:
if a in FIRST(i):
选择候选式
if a not in 每一个候选式的FIRST集
if a in FOLLOW(当前非终结符) and ε in FIRST(每一个候选式):
选择ε
else:
error();
下面就LL(1)分析法的两种具体实现方式进行分析。
递归下降分析法
递归下降分析法,顾名思义就是使用递归的思想去分析,具体的步骤:
对于一个文法G,对其每一个非终结符U构造一个递归过程,一般的,以非终结符的名字来命名这个子过程。所有子程序构造完成后,对指定文法,运行文法开始符号对应的子程序,返回匹配结果。
下面分析每一步的具体操作。
内容一:根据文法生成子程序
在实践这一部分的代码的时候,我想了挺久,没有思路,因为要构造指定文法的递归子程序,但在编码的时候,我们并不知道用户要输入的文法结构是怎么样的,所以这就产生了这么一个问题:如何用函数构造函数?实际上,如果我们能知道文法结构,那么就可以硬编码来生成对应的子程序。但是为了程序的良好拓展性,最后我用了这一方法:
1.create_function.py运行后, 用户输入一个指定文法
2.程序读取该文法的所有非终结符并且创建一个字典以所有非终结符作为key,其值为该非终结符对应的子程序的名称(一般和非终结符同名)
3.根据子程序的一般结构,定义每一个子程序不同的部分(比如子程序名称)
4.用python的文件操作,往新文件function.py中写入子程序的内容,包括必要的import,全局变量和每一个子程序,其中每一个子程序用一个循环来写入代码。
有话说: 在编写写入新文件的代码的时候需要记得’\n’,或者按行写入。
那么子程序的一般结构是什么呢?
例如:对于一个产生式E→AC|BD|ε,word为当前读入的符号
def E(...):
if word in FIRST(AC):
A(...)
C(...)
elif word in FIRST(BD):
B(...)
D(...)
elif word in FOLLOW(A):
不做其他操作
else:
error()
具体代码举例分析,完整代码见 链接:
引入需要用到的其他文件里的方法,这里我引用了我之前写的求FIRST \ FOLLOW集合的方法,这里的bunch就是要匹配的输入串,是在我们create这个子程序的时候由用户输入的,q为指针,用来指向当前匹配的符号。IP当初我用来检查每一个环节输出是否正确。
import syntactic_parser_demo
bunch = "q#"
q = 0
IP = bunch[0]
获取当前匹配字符到word中,判断匹配是否结束
global q
global IP
try:
word = bunch[q]
print("当前处理符号串符号:",word)
IP = word
except:
IP = "!"
return
if word == '#':
return
获取当前产生式的所有候选式,存在temp_split列表中,例如E→a|b|c,temp_split = [[‘a’],[‘b’],[‘c’]]
temp_or = []
temp_push = []
for k in range(len(parser)):
if parser[k] == '|':
temp_or.append(k)
temp_get = parser.index('→')
temp_push.append(temp_get)
temp_search = temp_push + temp_or
temp_split = []
for m in range(len(temp_search)):
if len(temp_search) == 1:
temp_split = [parser[temp_search[m] + 1:]]
else:
if m == (len(temp_search) - 1):
temp_split.append(parser[temp_search[m] + 1:])
else:
temp_split.append(parser[temp_search[m] + 1:temp_search[m + 1]])
判断是否需要递归调用其他子程序。
在这里我用eval(n[temp_n.index(j)])(i,lst_origin)来递归调用其他子程序,但实际上eval在某些场合需要谨慎使用。python中exec也可以执行一个字符串中的表达式例如:exec ("print('1')")
有话说: exec的返回值始终为 None 。
finish = 0
for n in temp_split:
if word == "".join(n[0]):
q += 1
temp_n = n[:]
if "'" in temp_n:
temp_n[temp_n.index("'") - 1] += "'"
temp_n.remove("'")
if "'" in n:
n[n.index("'") - 1] += '1'
n.remove("'")
if word in syntactic_parser_demo.get_first_bunch(temp_n,lst_origin):
finish = 1
for j in temp_n:
for i in lst_origin:
if "".join(i[:i.index('→')]) == j:
eval(n[temp_n.index(j)])(i,lst_origin)
break
break
获取FOLLOW集,判断第二个条件,判断第三个条件
dict_origin = syntactic_parser_demo.get_follow(lst_origin)
lst_follow_use = dict_origin["".join(parser[:parser.index('→')])]
if word in lst_follow_use:
finish = 1
if finish == 0:
error()
return IP
下面取一部分写入子程序的一些核心代码,完整代码见 链接
这里的写入部分我是将要写入的所有代码整合成一个字符串,再写入文件。写入的内容,先按照某一个子程序的结构,写出一个子程序的例子,再根据这个例子来写入代码。
# 创建相应的子程序并写入文件
back = open("function.py","a",encoding = "UTF-8")
back.seek(0)
back.truncate()
back.write("import syntactic_parser_demo\n\n")
back.write("bunch = " + "\"" + bunch + "\"" + "\nq = 0\nIP = bunch[0]\n\n")
for j in lst:
if "'" in j[:2]:
temp = "".join(j[0]) + "1"
else:
temp = "".join(j[0])
content = "def " + temp + "(word,parse,lst_origin):\n"\
+ " global q\n" + " global IP\n" + " try:\n"\
+ " word = bunch[q]\n" + " print(\"当前处理符号串符号:\",word)\n"\
+ " IP = word\n" + " except:\n" + " IP = \"!\"\n"\
+ " return\n" + " if word == '#':\n" + " return\n"\
+ " temp_or = []\n" + " temp_push = []\n" + " for k in range(len(parse)):\n"\
+ " if parse[k] == '|':\n" + " temp_or.append(k)\n" + " temp_get = parse.index('→')\n"\
+ " temp_push.append(temp_get)\n" + " temp_search = temp_push + temp_or\n" + " temp_split = []\n"\
+ " for m in range(len(temp_search)):\n" + " if len(temp_search) == 1:\n"\
+ " temp_split = [parse[temp_search[m] + 1:]]\n" + " else:\n"\
+ " if m == (len(temp_search) - 1):\n"\
+ " temp_split.append(parse[temp_search[m] + 1:])\n" + " else:\n"\
+ " temp_split.append(parse[temp_search[m] + 1:temp_search[m + 1]])\n"\
+ " finish = 0\n" + " for n in temp_split:\n" + " if word == \"\".join(n[0]):\n"\
+ " q += 1\n" + " temp_n = n[:]\n"\
+ " if \"\'\" in temp_n:\n" + " temp_n[temp_n.index(\"'\") - 1] += \"\'\"\n"\
+ " temp_n.remove(\"\'\")\n" + "" + " if \"\'\" in n:\n"\
+ " n[n.index(\"\'\") - 1] += '1'\n"\
+ " n.remove(\"\'\")\n"\
+ " if word in syntactic_parser_demo.get_first_bunch(temp_n,lst_origin):\n"\
+ " finish = 1\n"\
+ " for j in temp_n:\n" + " for i in lst_origin:\n"\
+ " if \"\".join(i[:i.index('→')]) == j:\n"\
+ " eval(n[temp_n.index(j)])(word,i,lst_origin)\n"\
+ " break\n" + " break\n"\
+ " dict_origin = syntactic_parser_demo.get_follow(lst_origin)\n"\
+ " lst_follow_use = dict_origin[\"\".join(parse[:parse.index('→')])]\n"\
+ " if word in lst_follow_use:\n" + " finish = 1\n"\
+ " if finish == 0:\n" + " error()\n\n"\
+ " return IP\n\n"
back.write(content)
back.write("def error():\n print('error.')\n return \n")
back.close()
内容二:调用文法开始符号所对应的子程序
接下来就是递归下降分析法的主程序部分,这部分比较简单,这里import function不能省略因为下面用的是eval来调用文法开始符号对应的子程序。
import function
def error():
print("error.")
return
if __name__ == "__main__":
lst_demo = [["E","→","T","E","'"],["E","'","→","+","T","E","'","|","ε"],["T","→","F","T","'"],
["T","'","→","*","F","T","'","|","ε"],["F","→","(","E",")","|","q"]]
print("当前内置文法:",lst_demo)
try:
ip = eval("function." + lst_demo[0][0])(lst_demo[0],lst_demo)
print("ip:",ip)
if ip == '#':
print("匹配文法成功")
else:
print("Error.")
except:
print("找不到子程序,即当前没有找到function.py或其为空文本,请先运行create_function.py创建.")
n = input("按任意键退出.")
n = input("按任意键退出.")
至此,递归下降分析法就完成了,可以少量修改代码让用户输入文法和输入串来达到更好的交互性。

预测分析法
预测分析法是LL(1)分析法的另一种实现方法,它不需要构造每一个子程序,而是通过一张表来关联非终结符和终结符,这张表就是预测分析表,预测分析表可以说是预测分析法的核心部分。
内容一:构造预测分析表
关于预测分析表的构造,参见我之前的一篇文章 构造预测分析表
内容二:预测分析法主程序
这里我们用一个栈来存放过程数据,主要步骤如下:
1.获取栈顶的元素A,获取输入串目前指针指向的元素a
2.若A = ‘#’ ,a = ‘#’ 则匹配成功
3.若A = a 但是A和a不为’#’,则pop栈顶元素,输入串指针+1
4.若A为非终结符,这查询预测分析表,把由A和a确定的产生式的右部从右往左依次压入到栈中,若右部是ε,那就不做操作
5.查找预测分析表得到预设的出错字符则调用error()
下面截取一些我写的代码进行讨论,完整代码见 链接
主程序的一些预备工作,这里我用列表来代替实现栈的一些功能
# 预测分析程序
import lexical_analysis_table
# 形参lst为所有产生式,bunch为待分析符号串
def control(lst,bunch):
table = lexical_analysis_table.get_table(lst) # 获取预测分析表
print("预测分析表:",table)
stack = [] # 工作栈
point = 0 # bunch指针
flag = True
s = table[-2] # 非终结符列表
l = table[-1] # 终结符列表
print("非终结符列表:",s,"终结符列表:",l)
count = 0
有话说: 这里要获取非终结符列表和终结符列表,他们的顺序是和表中的产生式有关的。
先把’#'压入stack中,再压入文法开始符号,然后获取输入串的第一个符号
stack.append('#')
stack.append("".join(lst[0][:lst[0].index('→')]))
temp_word = bunch[point]
然后正式开始匹配,根据上面步骤中的方法,用代码实现
while flag:
count += 1
remain_bunch = bunch[point:]
top_stack_word = stack.pop()
print("number:",count,"|stack:",stack,"|top_ele:",top_stack_word,"|剩余输入串:",remain_bunch)
if top_stack_word in l and top_stack_word != '#':
if top_stack_word == temp_word:
point += 1
temp_word = bunch[point]
else:
print("error.栈顶终结符和待分析终结符不一致.")
flag = False
elif top_stack_word == '#':
if top_stack_word == temp_word:
flag = False
print("分析成功.")
else:
print("error.栈和串没有同时结束分析.")
flag = False
elif top_stack_word in s:
# print("in s:",temp_word)
one = s.index(top_stack_word)
two = l.index(temp_word)
use_p = table[one][two][:]
# if use_p == 'ε':
# print("get a 'ε'")
if "'" in use_p:
index = use_p.index("'")
use_p[index - 1] += "'"
use_p.remove("'")
# print("ready:",use_p)
while True:
if len(use_p) == 1:
pop_word_temp = use_p
if pop_word_temp == "!":
print("error.未在预测分析表中找到替代.")
break
else:
stack.append(pop_word_temp)
else:
pop_word_temp = use_p.pop()
if pop_word_temp == 'ε':
print("ε值处理.")
elif pop_word_temp != "→":
stack.append(pop_word_temp)
else:
break
总结
- 同步更新至CSDN,仅作实验记录之用。
- 水平有限,文章有需要改正之处还望指出。