神经翻译笔记4扩展c. 2017-2019年间RNN和RNN语言模型的新进展

神经翻译笔记4扩展c. 2017-2019年间RNN和RNN语言模型的新进展

尽管在本文写作时（2020年4月），基于Transformer结构的预训练语言模型已经大杀四方，BERT都已经成为明日黄花，在其基础上衍生的各种变体，例如RoBERTa、ALBERT、BART等等长江后浪推前浪，使得基于RNN的语言模型更不再是语言模型领域的焦点。但是为了系列文章结构的完备性，本文以及下一篇文章仍然会介绍一些这方面的“新”工作和一些里程碑式的工作。本文将介绍2017至2019三年间，RNN体系结构及基于RNN的语言模型的一些新进展。

QuasiRNN

本文实际上发表于2016年，而且采用了CNN的思想，因此先不在本文介绍。在这里先立个flag，等本系列笔记进行到6时，再概述此工作。采取同样思想的亦有SRU，准备也到时再介绍

FS-RNN

FS-RNN (Fast-Slow RNN) [Mujika2017] 受两类RNN的启发

• 多（时间）尺度RNN：对于堆叠RNN中更高层的若干层，其被更新的次数越少（更不频繁），以此来获得信息的分层表示。由于高层参数更新变慢，因此计算起来更高效，梯度更新路径越短，越能捕捉长距离依赖
• 深度变换RNN (deep transition RNN)，其相邻两个隐藏状态之间引入了新的顺序连接层，以此来增加两个时间步之间变换函数的深度，进而学习更复杂的非线性变换

FS-RNN将两类网络结合起来，最简单的方式是

• 对底层RNN，引入深度变换（若干顺序连接层），称为“快层”
• 对高层RNN，降低更新频率，称为“慢层”

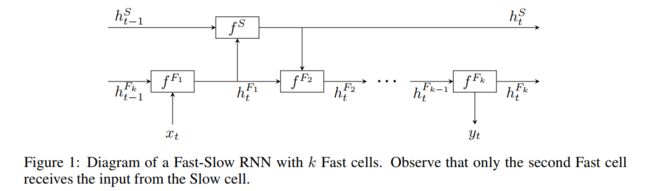
更形式化地讲，底层在两个时间步之间插入$k$个顺序连接的RNN神经元$F_1,\dots ,F_k$，高层只使用一个神经元$S$。$F_1$接收第$t$时间步的输入$x_t$，将输出传给$S$作为输入，$S$处理后将状态传给$F_2$，然后从$F_2$开始输出逐级传播下去，前一个$F_{i-1}$的输出作为后一个$F_i$的输入，到$F_k$输出概率分布$y_t$，如下图所示

记每个RNN神经元$Q$为一个可微函数$f^Q(h,x)$，其将上一步的隐藏状态$h$和输入$x$一起映射为一个新的隐藏状态，则

$$\begin{array}{rl}{h}_t^{F_1}& =f^{F_1}(h_{t-1}^{F_k},x_t)\\ h_t^S& =f^S(h_{t-1}^S,h_t^{F_1})\\ h_t^{F_2}& =f^{F_2}(h_t^{F_1},h_t^S)\\ h_t^{F_i}& =f^{F_i}\left(h_t^{F_{i-1}}\right)\mathrm{f}\mathrm{o}\mathrm{r}3\le i\le k\\ y_t& =\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(W{h}_t^{F_k}+b\right)\end{array}$$

文章使用LSTM作为基础的RNN神经元，在Penn Treebank和enwik8上均取得了不错的效果

Skip RNN

传统RNN和普通的带门控的RNN（例如LSTM）对长句表现都不好。[Campos2017]的思路是让网络学习输入序列中哪些样本可以解决目标问题，因此可以在训练时跳过一些状态的更新，可以减少对序列的操作

记RNN接受的输入序列$\mathbf{x}=(x_1,\dots ,x_T)$，每步向下传递的状态为$\mathbf{s}=(s_1,\dots ,s_T)$，有

$$s_t=\mathrm{R}\mathrm{N}\mathrm{N}(s_{t-1},x_t)$$

本文引入了一个额外的状态更新门$u_t\in \{0,1\}$，该门是完全二值的，只输出0或1，不像LSTM或GRU那样输出一个0到1的浮点数。当$u_t=1$时，该时刻状态更新；当$u_t=0$时，该时刻从前一时刻直接拷贝状态。$u_t$的结果由上一步产生的概率${\tilde{u}}_t\in [0,1]$决定，具体地

$$\begin{array}{rl}{u}_t& =f_{\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{z}\mathrm{e}}({\tilde{u}}_t)\\ s_t& =u_t\cdot \mathrm{R}\mathrm{N}\mathrm{N}(s_{t-1},x_t)+(1-u_t)\cdot s_{t-1}\\ \Delta {\tilde{u}}_t& =\sigma ({\mathbf{W}}_p{s}_t+{\mathbf{b}}_p)\\ {\tilde{u}}_{t+1}& =u_t\cdot \Delta {\tilde{u}}_t+(1-u_t)\cdot ({\tilde{u}}_t+\min (\Delta {\tilde{u}}_t,1-{\tilde{u}}_t))\end{array}$$

其中${\mathbf{W}}_p$是权重，${\mathbf{b}}_p$是偏置项，$\sigma$是sigmoid函数，$f_{\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{z}\mathrm{e}}:[0,1]\to \{0,1\}$是将输入映射为0或1的函数，本文使用了四舍五入法（round），也可以从伯努利分布随机采样。模型隐含了一个信息：如果连续跳过的状态越多，那么下一个状态就更可能被更新：

• 如果当前状态被跳过，那么下一个时间步的“预激活值”${\tilde{u}}_{t+1}$会增加$\Delta {\tilde{u}}_t$
• 如果当前状态被更新，那么累积的“预激活值”清零，重置为$\Delta {\tilde{u}}_t$

如果在某些场合下，可以为减少计算量额外牺牲精度，即为了让模型更倾向于少更新状态，则可以引入一个额外的损失项

$$L_{\mathrm{b}\mathrm{u}\mathrm{d}\mathrm{g}\mathrm{e}\mathrm{t}}=\lambda \cdot \sum _{t=1}^T{u}_t$$

有趣的是，本工作的三项实验均未在NLP任务上进行

高秩RNN语言模型MoS

[YangZhilin2017]将语言模型看作是一个矩阵分解问题。文章将自然语言$\mathcal{L}$定义为一个有限集合，集合中每个元素是一个有序对，由上下文和给定上下文后下一个标识符的分布两者组成，即

$$\mathcal{L}=\{(c_1,P^{\ast }(X|c_1)),\dots ,(c_N,P^{\ast }(X|c_N))\}$$

其中$N$是所有可能的上下文的数目。令$\mathcal{L}$中所有可能的标识符集合为$\{x_1,x_2,\dots ,x_M\}$，大小为$M$，则语言模型的目标是学习一个参数为$\theta$的模型分布$P_{\theta }(X|C)$以逼近真实分布$P^{\ast }(X|C)$。本文主要研究该模型的表示能力，即对给定的$\mathcal{L}$是否存在参数$\theta$，使得对$\mathcal{L}$中的所有$c$有$P_{\theta }(X|c)=P^{\ast }(X|c)$

对于RNN语言模型，$P_{\theta }(x|c)$由RNN的上下文向量（隐藏状态）${\mathbf{h}}_c$和词向量${\mathbf{w}}_x$决定，即

$$P_{\theta }(x|c)=\frac{\exp \{{\mathbf{h}}_c^{\mathsf{T}}{\mathbf{w}}_x\}}{{\sum }_{x^{\prime }}\exp \{{\mathbf{h}}_c^{\mathsf{T}}{\mathbf{w}}_{x^{\prime }}\}}$$

称${\mathbf{h}}_c^{\mathsf{T}}{\mathbf{w}}_x$为分对数logit。定义如下三个矩阵
$$\begin{gathered} {\mathbf{H}}_{\theta }=\left[\begin{array}{c}{\mathbf{h}}_{c_1}^{\mathsf{T}}\\ {\mathbf{h}}_{c_2}^{\mathsf{T}}\\ \cdots \\ {\mathbf{h}}_{c_N}^{\mathsf{T}}\end{array}\right]\in {\mathbb{R}}^{N\times d};{\mathbf{W}}_{\theta }=\left[\begin{array}{c}{\mathbf{w}}_{x_1}^{\mathsf{T}}\\ {\mathbf{w}}_{x_2}^{\mathsf{T}}\\ \cdots \\ {\mathbf{w}}_{x_M}^{\mathsf{T}}\end{array}\right]\in {\mathbb{R}}^{M\times d} \\ \mathbf{A}=\left[\begin{array}{cccc}\log P^{\ast }(x_1|c_1)& \log P^{\ast }(x_2|c_1)& \cdots & \log P^{\ast }(x_M|c_1)\\ \log P^{\ast }(x_1|c_2)& \log P^{\ast }(x_2|c_2)& \cdots & \log P^{\ast }(x_M|c_2)\\ ⋮& ⋮& \ddots & ⋮\\ \log P^{\ast }(x_1|c_N)& \log P^{\ast }(x_2|c_N)& \cdots & \log P^{\ast }(x_M|c_N)\end{array}\right]\in {\mathbb{R}}^{N\times M} \end{gathered}$$

其中${\mathbf{H}}_{\theta }$、${\mathbf{W}}_{\theta }$和$\mathbf{A}$的每一行分别是上下文向量、词向量和真实分布中概率的对数值。对不同的参数$\theta$，${\mathbf{H}}_{\theta }$和${\mathbf{W}}_{\theta }$也会不同

定义矩阵集合$F(\mathbf{A})$为$\mathbf{A}$每行各自加一增量得到的矩阵的集合。形式化表示为

$$F(\mathbf{A})=\{\mathbf{A}+{\mathbf{\Lambda }\mathbf{J}}_{N,M}|\mathbf{\Lambda }\in {\mathbb{R}}^{N\times N}\}$$

其中$\mathbf{\Lambda }$为对角矩阵。$F(\mathbf{A})$就是让$\mathbf{A}$第$i$行每个元素都增加一个增量${\mathbf{\Lambda }}_{ii}$

文章根据$F(\mathbf{A})$的两个性质和一条引理（具体内容略）将问题转化为：是否存在一个参数$\theta$和矩阵${\mathbf{A}}^{\prime }\in F(\mathbf{A})$，使得
$${\mathbf{H}}_{\theta }{\mathbf{W}}_{\theta }^{\mathsf{T}}={\mathbf{A}}^{\prime }$$

这实际上是一个矩阵分解问题。如果存在一个合法的矩阵分解，则${\mathbf{H}}_{\theta }{\mathbf{W}}_{\theta }^{\mathsf{T}}$的秩不应该比${\mathbf{A}}^{\prime }$的秩小，而${\mathbf{H}}_{\theta }{\mathbf{W}}_{\theta }^{\mathsf{T}}$秩的上界为$d$。文章再次推导并形式化提出了“Softmax瓶颈”问题，即

如果$d<\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}({\mathbf{A}}^{\prime })-1$，则对任意函数族$\mathcal{U}$和任意模型参数$\theta$，$\mathcal{L}$中都有一个上下文$c$使得$P_{\theta }(X|c)\ne P^{\ast }(X|c)$

更白话的解释是，当$d$太小时，softmax没有足够能力表示真实的数据分布。然而，根据一些直觉和经验观察，对任何自然语言$\mathcal{L}$来说，$\mathbf{A}$可能都是高秩的，即在目前的实践中都有$d\ll \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}(\mathbf{A})$。一种对策是使用非参数模型，例如Ngram语言模型，不过这种模型表示能力太高会损失泛化能力

本文提出的方法是在模型里计算$K$个softmax分布，然后将他们的结果加权输出，即

$$\begin{array}{rl}{P}_{\theta }(x|c)& =\sum _{k=1}^K{\pi }_{c,k}\frac{\exp \{{\mathbf{h}}_{c,k}^{\mathsf{T}}{\mathbf{w}}_x\}}{{\sum }_{x^{\prime }}\exp \{{\mathbf{h}}_{c,k}^{\mathsf{T}}{\mathbf{w}}_{x^{\prime }}\}}\\ {\pi }_{c_t,k}& =\frac{\exp \{{\mathbf{w}}_{\pi ,k}^{\mathsf{T}}{\mathbf{g}}_t\}}{{\sum }_{k^{\prime }=1}^K\exp \{{\mathbf{w}}_{\pi ,k^{\prime }}^{\mathsf{T}}{\mathbf{g}}_t\}}\\ {\mathbf{h}}_{c_t,k}& =\tanh ({\mathbf{W}}_{h,k}{\mathbf{g}}_t)\end{array}$$

其中${\mathbf{g}}_t$是由加在输入$\mathbf{X}$上的RNN得到的隐藏状态（感觉相当于本节最开始引入的$\mathbf{h}$），${\mathbf{w}}_{\pi ,k}$和${\mathbf{W}}_{h,k}$都是模型参数。本文称这种方法为“softmax混合模型”（Mixture of Softmaxes，缩写MoS）

本工作的直接后继是Mixtape [YangZhilin2019]，不过模型更加复杂，这里就不介绍了

IndRNN

由于RNN中各时间步内部共享一个权重矩阵$\mathbf{U}$（正文中的$\mathbf{W}$），因此会很容易带来梯度消失或梯度爆炸问题，而且很难解释和理解单个神经元所扮演的角色。此外，每个时间步展开时所进行的矩阵乘法也不好并行化，使得网络对长序列的处理非常耗时。[LiShuai2018] 提出将这个$\mathbf{U}$替换成一个$d$维向量$\mathbf{u}$（$d$为每层神经元的个数），即第$t$时刻隐藏状态为

$${\mathbf{h}}^{(t)}=\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\left({\mathbf{W}\mathbf{x}}^{(t)}+\mathbf{u}\odot {\mathbf{h}}^{(t-1)}+\mathbf{b}\right)$$

这使得每一层的各个神经元都相互独立，都只从前一个时刻自身的隐藏状态接收信息，不被其他神经元影响，如下图所示。因此网络被称为“独立循环神经网络”（Independent RNN, IndRNN）。IndRNN常用ReLU作为激活函数

对第$n$个神经元，隐藏状态为

$$h_n^{(t)}=\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\left({\mathbf{w}}_n{\mathbf{x}}^{(t)}+u_n{h}_n^{(t-1)}+b_n\right)$$

假设对时刻$T$的目标函数是$J_n$，则其反向传播到时刻$t$的梯度为

$$\begin{array}{rl}\frac{\partial J_n}{\partial h_n^{(t)}}& =\frac{\partial J_n}{\partial h_n^{(T)}}\frac{\partial h_n^{(T)}}{\partial h_n^{(t)}}=\frac{\partial J_n}{\partial h_n^{(T)}}\prod _{k=t}^{T-1}\frac{\partial h_n^{(k+1)}}{\partial h_n^{(k)}}\\ & =\frac{\partial J_n}{\partial h_n^{(T)}}\prod _{k=t}^{T-1}{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}_n^{{}^{\prime }(k+1)}{u}_n=\frac{\partial J_n}{\partial h_n^{(T)}}{u}_n^{T-t}\prod _{k=t}^{T-1}{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}_n^{{}^{\prime }(k+1)}\end{array}$$

这里只依赖两项：标量$u_n$的指数项（正则化更容易）和激活函数的逐元素导数（一般都有界）。由于标量$u_n$在训练过程中只根据学习率被微调，而不是像矩阵一样其乘积由特征值决定（而特征值很容易剧烈变化），因此IndRNN的训练过程更鲁棒。为了避免梯度消失，只需要让$|u_n|>0$即可。而且由于各个$u_n$相对独立，因此很难出现所有$u_n$都为0的情况，不用刻意限制，只需要让$|u_n|\le \sqrt[(T-t)]{\gamma }$来防止梯度爆炸即可（$\gamma$是不让爆炸发生的最大梯度）。如果只是要做文本分类，只需要长期记忆，则需要提高$|u_n|$的下界使得梯度在$T-t$个时间步后仍然有效。记最小的有效梯度为$ϵ$，则此时需要将权重初始化在区间$[\sqrt[(T-t)]{ϵ},\sqrt[(T-t)]{\gamma }]$内。（注意，这里对关键结论有所省略，仅讨论激活函数为ReLU的情况）

将基本IndRNN单元和批归一化BN相结合作为一个原子单元，并将若干原子单元堆叠，可以组成更深的IndRNN网络。进一步，可以在纵向各层之间引入残差连接，进一步增强深层网络的稳定性。记第$l$层第$t$步的残差连接为${\mathcal{F}}_l^{(t)}$，第$l$层第$t$步的输出特征为$x_l^{(t)}$，有
$$x_l^{(t)}=x_{l-1}^{(t)}+{\mathcal{F}}_l^{(t)}\left(x_{l-1}^{(t)}\right)$$
或者可以将残差连接（相加操作）改成连接操作$\mathcal{C}$，此时可以看做是将前面各层的特征都组合起来，即
$$x_l^{(t)}=\mathcal{C}\left(x_{l-1}^{(t)},{\mathcal{F}}_l^{(t)}\left(x_{l-1}^{(t)}\right)\right)$$
称为稠密连接IndRNN（densely connected IndRNN）。三种体系结构如下图所示

IndRNN各时间步可独立计算${\mathbf{W}\mathbf{x}}^{(t)}$，而$\mathbf{u}\odot {\mathbf{h}}^{(t-1)}$计算量较小，因此并行化得到了提高。实验表明IndRNN在序列极长（上千步）时仍然能快速收敛，且能叠加多层（12层）

ON-LSTM

尽管语言读写时展现出线性的表象，但是其底层结构并非线性，而是树形、分层的。将树形结构引入深度神经网络，可以获得一个分层的表示结果，而且可以对语言本身的组合现象建模，处理长期依赖问题。在统计自然语言处理中，使用有监督的句法分析器产生句法树，已经是一个经典方向，而且一些思想也被引入到了深度学习中。但是很多语言没有大量有标注的数据，一些领域里语言结构也不规则（例如推特），而且随着时间的变化语言结构也会缓慢改变。另一方面，让模型从语料中自动归纳语法仍然是一个开放性问题。[ShenYikang2018]提出了一种称为“有序神经元”（ordered neurons）的方法，通过无监督语法分析让高层神经元学习长期信息，而底层神经元学习短期信息。高层神经元和底层神经元通过控制神经元的更新频率来做区分：高层神经元更新更少，而底层更新更多。使用这种神经元构成的网络，称为ON-LSTM。ON-LSTM与语法树的关系大致如下图所示，图中最顶层节点只在第一步更新，代表了整个句子的信息；第二层节点在第1、2步更新，而第三层节点由于对应单词词性（语法树叶子节点），需要每步都被更新。节点的更新顺序是预先定义的，作为模型结构的一部分

然而，经典LSTM各个节点的门控单元都是独立的，很难体现分层信息，因此需要修改来引入这种依赖关系。本文提出了一种新的激活函数$\mathrm{c}\mathrm{u}\mathrm{m}\mathrm{a}\mathrm{x}$，定义为

$$\hat{\mathbf{g}}=\mathrm{c}\mathrm{u}\mathrm{m}\mathrm{a}\mathrm{x}(\dots )=\mathrm{c}\mathrm{u}\mathrm{m}\mathrm{s}\mathrm{u}\mathrm{m}(\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}(\dots ))$$

其中$\mathrm{c}\mathrm{u}\mathrm{m}\mathrm{s}\mathrm{u}\mathrm{m}$为累加函数。该激活函数使得向量$\hat{\mathbf{g}}$表现出一种二元门$(0,\dots ,0,1,\dots ,1)$的形态，其可以将RNN神经元的状态分成两段，进而对两段使用不同的更新方法。记随机变量$d$为$\hat{\mathbf{g}}$两段的分隔点（第一次出现1的位置）。实际上，$d$就是$\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}(\dots )$结果中最大分量所在的索引位置

就此，文章引入两个新的门，主遗忘门${\tilde{\mathbf{f}}}^{(t)}$和主更新门${\tilde{\mathbf{i}}}^{(t)}$：（这里仍然是用$\mathbf{h}$表示隐藏向量）

$$\begin{array}{rl}{\tilde{\mathbf{f}}}^{(t)}& =\mathrm{c}\mathrm{u}\mathrm{m}\mathrm{a}\mathrm{x}\left({\mathbf{W}}_{\tilde{f}}{\mathbf{x}}^{(t)}+{\mathbf{U}}_{\tilde{f}}{\mathbf{h}}^{(t-1)}+{\mathbf{b}}_{\tilde{f}}\right)\\ {\tilde{\mathbf{i}}}^{(t)}& =1-\mathrm{c}\mathrm{u}\mathrm{m}\mathrm{a}\mathrm{x}\left({\mathbf{W}}_{\tilde{i}}{\mathbf{x}}^{(t)}+{\mathbf{U}}_{\tilde{i}}{\mathbf{h}}^{(t-1)}+{\mathbf{b}}_{\tilde{i}}\right)\end{array}$$

其中主遗忘门是递增的（在某个位置之前的元素都是0，之后的元素都是1），而主更新门是递减的。整个ON-LSTM的更新规则为

$$\begin{array}{rl}{\mathbf{f}}^{(t)}& =\sigma \left({\mathbf{W}}_f{\mathbf{x}}^{(t)}+{\mathbf{U}}_f{\mathbf{h}}^{(t-1)}+{\mathbf{b}}_f\right)\\ {\mathbf{i}}^{(t)}& =\sigma \left({\mathbf{W}}_i{\mathbf{x}}^{(t)}+{\mathbf{U}}_i{\mathbf{h}}^{(t-1)}+{\mathbf{b}}_i\right)\\ {\mathbf{o}}^{(t)}& =\sigma \left({\mathbf{W}}_o{\mathbf{x}}^{(t)}+{\mathbf{U}}_o{\mathbf{h}}^{(t-1)}+{\mathbf{b}}_o\right)\\ {\hat{\mathbf{c}}}^{(t)}& =\tanh \left({\mathbf{W}}_c{\mathbf{x}}^{(t)}+{\mathbf{U}}_c{\mathbf{h}}^{(t-1)}+{\mathbf{b}}_c\right)\\ {\tilde{\mathbf{f}}}^{(t)}& =\mathrm{c}\mathrm{u}\mathrm{m}\mathrm{a}\mathrm{x}\left({\mathbf{W}}_{\tilde{f}}{\mathbf{x}}^{(t)}+{\mathbf{U}}_{\tilde{f}}{\mathbf{h}}^{(t-1)}+{\mathbf{b}}_{\tilde{f}}\right)\\ {\tilde{\mathbf{i}}}^{(t)}& =1-\mathrm{c}\mathrm{u}\mathrm{m}\mathrm{a}\mathrm{x}\left({\mathbf{W}}_{\tilde{i}}{\mathbf{x}}^{(t)}+{\mathbf{U}}_{\tilde{i}}{\mathbf{h}}^{(t-1)}+{\mathbf{b}}_{\tilde{i}}\right)\\ {\mathbf{\omega }}^{(t)}& ={\tilde{\mathbf{f}}}^{(t)}\circ {\tilde{\mathbf{i}}}^{(t)}\\ {\hat{\mathbf{f}}}^{(t)}& ={\mathbf{f}}^{(t)}\circ {\mathbf{\omega }}^{(t)}+\left({\tilde{\mathbf{f}}}^{(t)}-{\mathbf{\omega }}^{(t)}\right)={\tilde{\mathbf{f}}}^{(t)}\circ \left({\mathbf{f}}^{(t)}\circ {\tilde{\mathbf{i}}}^{(t)}+1-{\tilde{\mathbf{i}}}^{(t)}\right)\\ {\hat{\mathbf{i}}}^{(t)}& ={\mathbf{i}}^{(t)}\circ {\mathbf{\omega }}^{(t)}+\left({\tilde{\mathbf{i}}}^{(t)}-{\mathbf{\omega }}^{(t)}\right)={\tilde{\mathbf{i}}}^{(t)}\circ \left({\mathbf{i}}^{(t)}\circ {\tilde{\mathbf{f}}}^{(t)}+1-{\tilde{\mathbf{f}}}^{(t)}\right)\\ {\mathbf{c}}^{(t)}& ={\hat{\mathbf{f}}}^{(t)}\circ {\mathbf{c}}^{(t-1)}+{\hat{\mathbf{i}}}^{(t)}\circ {\hat{\mathbf{c}}}^{(t)}\\ {\mathbf{h}}^{(t)}& ={\mathbf{o}}^{(t)}\circ \tanh \left({\mathbf{c}}^{(t)}\right)\end{array}$$

其背后的直觉如下（假设所有主门每个元素都是0或1）

• 主遗忘门${\tilde{\mathbf{f}}}^{(t)}$控制模型的擦除行为。假设其分隔点为$d_f^{(t)}$，根据${\hat{\mathbf{f}}}^{(t)}$和${\mathbf{c}}^{(t)}$的更新公式，前一个单元传来的状态${\mathbf{c}}^{(t-1)}$的前$d_f^{(t)}$个神经元都被擦除。在语法树中，这意味着前一个成分已经被处理完毕
• 主输入门${\tilde{\mathbf{i}}}^{(t)}$控制模型的写入行为。假设其分隔点为$d_i^{(t)}$，该值若大则说明当前输入包含长期信息，需要保存若干个时间步
• 两个主门的逐元素乘积${\mathbf{\omega }}^{(t)}$表示它们交叠的部分。当交叠存在时，这一段里的神经元编码的成分是不完全的，通过标准LSTM来更新

（所以文章两个主门的作用是预测每一步的分隔点，通过分隔点控制信息的更新。分隔点的位置决定了两个0-1向量，但是0-1向量是离散的，不好求导，所以通过softmax来近似——这也是文章在4.1节后面文字所想表达的内涵？看了下面引用的苏剑林的博客，自己的一点概括，不一定准确）

由于主门只做大粒度的控制，因此可以让其维度小一点。设隐藏状态的维度为$D$，这里所有主门的维度都是$D/C$的，其中$C$是一个超参数。在与LSTM遗忘门和输入门逐元素相乘时，将主门的每个分量重复$C$次，即每$C$个神经元由一个主门控制

实验表明，ON-LSTM不仅提高了语言模型的效果，还能无监督地学到句子的语法结构

ON-LSTM是ICLR 2019的最佳论文之一。本节仅是对原文做的一个简单记录，更详细的分析可以参考苏剑林：ON-LSTM用有序神经元表达层次结构

Mogrifier LSTM

Mogrifier LSTM[Melis2019]期望通过引入额外的门控机制，使得模型对当前输入的信息能够结合上文进行缩放，进而得到一个受上文影响的输入表示。对于原始的LSTM，输入门${\mathbf{i}}^{(t)}$可以看做是对${\tilde{\mathbf{c}}}^{(t)}$的每行都做了一个放缩（不看非线性操作$\tanh$）（因为${\mathbf{c}}^{(t)}$的更新里有一项是${\tilde{\mathbf{c}}}^{(t)}\odot {\mathbf{i}}^{(t)}$）。Mogrifier LSTM更进一步，使得LSTM的所有权重矩阵$\mathbf{W}$和$\mathbf{U}$的每一列都被缩放一个因子，且缩放程度和上下文相关。具体地，在计算各个门之前，Mogrifier LSTM让输入${\mathbf{x}}^{(t)}$（简记为$\mathbf{x}$）和上一步隐藏状态${\mathbf{h}}^{(t-1)}$（记为${\mathbf{h}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{v}}$）交互影响，即
$$\begin{array}{rl}\mathrm{M}\mathrm{o}\mathrm{g}\mathrm{r}\mathrm{i}\mathrm{f}\mathrm{y}(\mathbf{x},{\mathbf{c}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{v}},{\mathbf{h}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{v}})& =\mathrm{L}\mathrm{S}\mathrm{T}\mathrm{M}({\mathbf{x}}^{\uparrow },{\mathbf{c}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{v}},{\mathbf{h}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{v}}^{\uparrow })\\ {\mathbf{x}}^{\uparrow }和{\mathbf{h}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{v}}^{\uparrow }是如下& 迭代过程最终一步的结果\\ {\mathbf{x}}^i& =2\sigma \left({\mathbf{Q}}^i{\mathbf{h}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{v}}^{i-1}\right)\odot {\mathbf{x}}^{i-2}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{o}\mathrm{d}\mathrm{d}i\in [1\dots r]\\ {\mathbf{h}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{v}}^i& =2\sigma \left({\mathbf{R}}^i{\mathbf{x}}^{i-1}\right)\odot {\mathbf{h}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{v}}^{i-2}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{n}i\in [1\dots r]\\ {\mathbf{x}}^{-1}& =\mathbf{x},{\mathbf{h}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{v}}^0={\mathbf{h}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{v}}\end{array}$$

$r\in \mathbb{N}$是模型的超参数，定义迭代过程的轮数。当$r=0$时，Mogrifier LSTM退化为标准LSTM。为了减少模型参数，通常将${\mathbf{Q}}^i$和${\mathbf{R}}^i$分解成两个低秩矩阵的乘积。实践表明，$r$为5或6，低秩矩阵的秩在40到90之间时，效果最好。文章尝试了两种变体，分别为

• ${\mathbf{Q}}^i$和${\mathbf{R}}^i$使用满秩矩阵
• ${\mathbf{x}}^i$更新时不再依赖前一次迭代的${\mathbf{h}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{v}}^{i-1}$，而是都依赖初始的${\mathbf{h}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{v}}$。${\mathbf{h}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{v}}^i$同理

两种变体效果都不太好

本文在PTB和MWC两个语言模型任务上进行了实验，都取得了不错的效果。此外，文章通过“逆序拷贝”任务（读入一个字符串，遇到某个特殊字符时，倒序输出所有接收到的输入），验证模型的确可以根据上下文放大输入表示中有用的信息，减少无用的信息，从而降低输入嵌入矩阵的维度

最后，文章认为以下几项假说不能解释mogrifier的有效性，包括

• “Mogrifier LSTM受益于对$\mathbf{x}$和${\mathbf{h}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{v}}$进行缩放”：否。对LSTM做缩放，且使缩放因子可学习，并没有提升LSTM的效果
• “Mogrifier LSTM受益于让优化过程更容易”：否。没有观察到
• “常见的语言模型正则化手段之一是让输入输出共享词嵌入矩阵，这个限制太大，而mogrifier放松了这样的限制”：否。分开学习输入输出嵌入矩阵，mogrifier仍然有效
• “Mogrifier LSTM受益于低秩矩阵分解”：否。使用满秩矩阵虽然降低了效果，但是仍然比普通LSTM好
• “Mogrifier LSTM在罕见词上表现更佳”：否。逆序拷贝任务不存在罕见词问题，mogrifier LSTM效果仍然更好
• “Mogrifier LSTM只在英语上效果好”：否。MWC（多语Wiki数据集）的效果推翻了这种说法
• “Mogrifier LSTM更能处理长距离依赖”：否。在句子级语言模型上mogrifier LSTM效果也很好

参考文献

• [Mujika2017] Mujika, A., Meier, F., & Steger, A. (2017). Fast-slow recurrent neural networks. In Advances in Neural Information Processing Systems (NeurIPS 2017) (pp. 5915-5924).
• [Campos2017] Campos, V., Jou, B., Giró-i-Nieto, X., Torres, J., & Chang, S. F. (2017). Skip rnn: Learning to skip state updates in recurrent neural networks. arXiv preprint arXiv:1708.06834. (Published in ICLR 2018).
• [YangZhilin2017] Yang, Z., Dai, Z., Salakhutdinov, R., & Cohen, W. W. (2017). Breaking the softmax bottleneck: A high-rank RNN language model. arXiv preprint arXiv:1711.03953. (Published in ICLR 2018).
• [YangZhilin2019] Yang, Z., Luong, T., Salakhutdinov, R. R., & Le, Q. V. (2019). Mixtape: Breaking the Softmax Bottleneck Efficiently. In Advances in Neural Information Processing Systems (NeurIPS 2019) (pp. 15922-15930).
• [LiShuai2018] Li, S., Li, W., Cook, C., Zhu, C., & Gao, Y. (2018). Independently recurrent neural network (indrnn): Building a longer and deeper rnn. In Proceedings of the IEEE conference on computer vision and pattern recognition (CVPR2018) (pp. 5457-5466).
• [ShenYikang2018] Shen, Y., Tan, S., Sordoni, A., & Courville, A. (2018). Ordered neurons: Integrating tree structures into recurrent neural networks. arXiv preprint arXiv:1810.09536.
• [Melis2019] Melis, G., Kočiský, T., & Blunsom, P. (2019). Mogrifier lstm. arXiv preprint arXiv:1909.01792. (Pulished in ICLR 2020)