神经翻译笔记3扩展b. 自动微分

神经翻译笔记3扩展b. 自动微分

本文无说明的部分（包括配图）均是翻译/演绎自：

Baydin, A. G., Pearlmutter, B. A., Radul, A. A., & Siskind, J. M. (2017). Automatic differentiation in machine learning: a survey. Journal of machine learning research, 18(153), 1-43.

不过没有包含若干偏理论的内容

其它引用会单独注明

---

引言

如前所示，在训练神经网络时，需要计算损失函数对网络参数的梯度，其中会涉及到很多次导数的计算。一般来讲，编程计算导数有四种做法

• 手动微分（manual differentiation），手动推出导数是什么样，然后硬编码。这种做法既耗时也容易出错，还没有灵活性

• 数值微分（numerical differentiation），利用数值代数方法逼近函数的导数值。这种方法存在舍入误差和截断误差，而且扩展性差，在深度学习需要计算百万量级参数的梯度时不适用

• 符号微分（symbolic differentiation）。通常是计算机代数系统采用，例如Mathematica, Maxima和Maple等等。这种方法试图给出给定表达式导数的代数形式，但是会导致表达式爆炸的现象。而且其底层依赖一个封闭的表达式库，给方法求解问题的范畴施加了局限

• 自动微分（automatic differentiation），或者也被称为算法微分（algorithmic differentiation），是本文的主题

自动微分不是什么

自动微分不是数值微分

这里先介绍一下数值微分的计算思想。考虑到导数的定义，如果一个函数$y=f(x)$在点$x_0$处可导，那么其在该点处的导数为
$$f^{\prime }(x_0)=\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$$
因此可以使用导数的定义，使用一个特别小的$\Delta x$（例如$10^{-6}$）来计算导数。但是这种做法会产生偏差。假设以$h$代替$\Delta x$，那么近似计算$f$在$x$点处的导数为
$$f^{\prime }(x)\approx \frac{f(x+h)-f(x)}{h}$$
而$f(x+h)$关于$x$的泰勒展开为
$$f(x+h)=f(x)+h{f}^{\prime }(x)+\frac{h^2}{2}{f}^{\prime \prime }(\xi ),\xi \in (x,x+h)$$
因此会存在一个$-\frac{h}{2}{f}^{\prime \prime }(\xi )$的误差，该误差称为截断误差（truncation error）。这种方法称为前向差分法（forward differencing），注意其截断误差是$O(h)$的
对于前向微分法，有一种改进的方法可以提高估计的准确率，称为中心差分法（centered differencing）
$$f^{\prime }(x)\approx \frac{f(x+h)-f(x-h)}{2h}$$
（验证内容来自于马里兰大学学院市分校（UMD）数值分析课AMSC466的讲义）下面验证该式有更好的准确度。该式右侧的泰勒展开为
$$\begin{array}{rl}f(x+h)& =f(x)+h{f}^{\prime }(x)+\frac{h^2}{2}{f}^{\prime \prime }(x)+\frac{h^3}{6}{f}^{\prime \prime \prime }({\xi }_1)\\ f(x-h)& =f(x)-h{f}^{\prime }(x)+\frac{h^2}{2}{f}^{\prime \prime }(x)-\frac{h^3}{6}{f}^{\prime \prime \prime }({\xi }_1)\end{array}$$
其中${\xi }_1\in (x,x+h),{\xi }_2\in (x-h,x)$。因此
$$f^{\prime }(x)=\frac{f(x+h)-f(x-h)}{2h}-\frac{h^2}{12}[f^{\prime \prime \prime }({\xi }_1)+f^{\prime \prime \prime }(x_2)]$$
即中心差分法的截断误差是$-\frac{h^2}{12}[f^{\prime \prime \prime }({\xi }_1)+f^{\prime \prime \prime }({\xi }_2)]$。假设三阶导数在区间$[x-h,x+h]$连续，那么由介值定理，存在点$\xi \in (x-h,x+h)$使得
$$f^{\prime \prime \prime }(\xi )=\frac{1}{2}[f^{\prime \prime \prime }({\xi }_1)+f^{\prime \prime \prime }({\xi }_2)]$$
因此
$$f^{\prime }(x)=\frac{f(x+h)-f(x-h)}{2h}-\frac{h^2}{6}{f}^{\prime \prime \prime }(\xi )$$
即中心差分法的截断误差是$O(h^2)$的。当$h$很小时，该误差小于前向差分法的误差 $■$

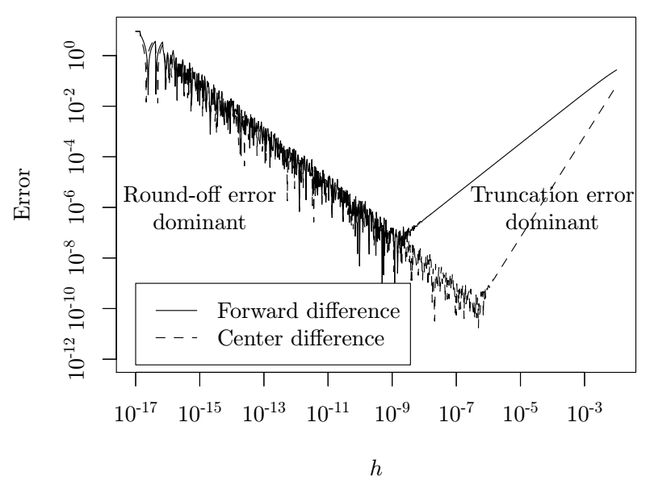
**数值微分的缺点是存在截断误差和舍入误差，同时计算太慢。**比较不幸的是，随着$h$大小的变化，截断误差和舍入误差的变化趋势相反：当$h$趋近于0时，截断误差也趋近于0，但是舍入误差会慢慢增大，反之相反。下图给出了函数$f(x)=64x(1-x)(1-2x{)}^2(1-8x+8x^2{)}^2$使用数值微分计算在点$x_0=0.2$的导数时误差随$h$变化的图像。

此外还需注意一点：当参数是标量时，前向差分法和中心差分法的计算代价相同。不过当参数是向量时，使用中心差分法计算函数$f:{\mathbb{R}}^n\to {\mathbb{R}}^m$的雅可比矩阵需要额外$mn$个计算量。尤其在深度学习领域，对于$n$维向量，这种$O(n)$的计算量是算法的主要瓶颈，而误差已经不重要了

自动微分不是符号微分

符号微分将输入式子表达为一个表达式树，然后对每个节点使用一些预先设置好的规则做转换。符号微分可以帮助人们更深入地了解问题域的结构，有时候还能给出极值条件的解析解，不过它们会产生指数量级的表达式，因此计算起来效率很低。考虑函数$h(x)=f(x)g(x)$和微分的乘法法则
$$\frac{d}{dx}(f(x)g(x))⇝\left(\frac{d}{dx}f(x)\right)g(x)+f(x)\left(\frac{d}{dx}g(x)\right)$$
由于$h$是两个函数的乘积，因此$h(x)$和$\frac{d}{dx}h(x)$有相同的成分，分别是$f(x)$和$g(x)$。此外，注意乘法法则的右式，$f(x)$和$\frac{d}{dx}f(x)$分别出现在不同的位置，因此如果继续符号微分$f(x)$，然后将导数代入，那么就会出现很多冗余的表达式，它们既出现在$f(x)$的位置，也出现在$\frac{d}{dx}f(x)$的位置。下图给出了对表达式$l_{n+1}=4l_n(1-l_n),l_1=x$在$n=\{1,2,3,4\}$时的结果，可以注意在$n=4$时，表达式$(1-8x+8x^2)$在$\frac{d}{dx}{l}_n$中出现了多少次

从图中可以看到，符号微分可以很容易产生指数量级的符号表达式，因此需要很长时间来求值。这种问题称为表达式膨胀（expression swell）

当我们只需要得到微分结果一个准确的数值表示，而不关心它具体的代数形式时，理论上可以把中间子表达式的结果存在内存里，这样就可以极大化简计算过程。更进一步地，可以将微分操作和化简操作交替进行，这样效率更高。这种交替操作的思想构成了自动微分的基础：在基本操作的层面上使用符号微分，保留中间的数值结果，同步计算主函数——这其实就是自动微分的前向累积模式，将在下一节介绍

自动微分及其主要模式

自动微分的所有数值计算最终都是一些有限原子操作的组合，而这些基本操作的导数通常是已知的。自动微分会通过链式法则，将原子表达式的微分结果捏合起来，给出整个表达式的求导结果。对于给定的表达式，总可以将其整理成原子操作的计算序列（evaluation trace），或者称为Wengert序列。对于函数$f:{\mathbb{R}}^n\to {\mathbb{R}}^m$，假设其输入为$x_1,\dots ,x_n$，输出为$y_1,\dots ,y_m$，那么变量$v_i$分属于以下三种情况

• 变量$v_{i-n}=x_i,i=1,2,\dots ,n$是输入变量
• 变量$v_i,i=1,2,\dots ,l$是工作（中间）变量
• 变量$y_{m-i}=v_{l-i},i=m-1,\dots ,0$是输出变量

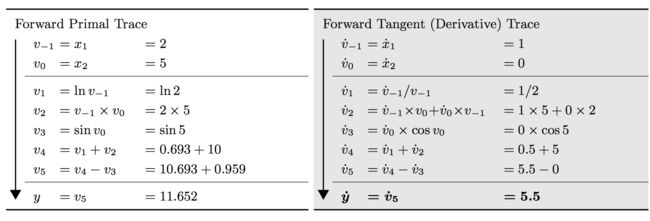
下图给出了表达式$y=f(x_1,x_2)=\ln (x_1)+x_1{x}_2-\sin (x_2)$的计算序列所对应的计算图，计算图可以清楚表示中间变量之间的依赖关系

其中各个变量的定义参见下表（假设输入$(x_1,x_2)=(2,5)$）

变量	计算方式	值
$v_{-1}$	$x_1$	2
$v_0$	$x_2$	5
$v_1$	$\ln v_{-1}$	$\ln 2$
$v_2$	$v_{-1}\times v_0$	$2\times 5$
$v_3$	$\sin v_0$	$\sin 5$
$v_4$	$v_1+v_2$	0.693 + 10
$v_5$	$v_4-v_3$	10.693 + 0.959
$y$	$v_5$	11.652

计算序列是自动微分的基础。注意自动微分不只可以计算闭合形式表达式的微分，对使用了分支、循环、递归、函数调用的算法也适用，其原因就是任何有关数值计算的逻辑最后都可以表达成一个基于数值的计算序列，包含确定的输入、中间变量和输出。而只要有了这些信息，就可以使用链式法则计算导数

前向模式（Forward mode）

前向模式是一种比较简单的自动微分方法。对上面给出的例子，若要计算$f$对$x_1$的导数，先要计算所有中间变量对$x_1$的导数，记为
$${\dot{v}}_i=\frac{\partial v_i}{\partial x_1}$$
这样，在向前计算每个$v_i$的值时，也能同时计算对应的${\dot{v}}_i$，如下表所示

这种做法可以很容易推广到函数$f:{\mathbb{R}}^n\to {\mathbb{R}}^m$的雅可比矩阵的计算，其输入是$n$个独立变量$x_i$，输出是$m$个独立变量$y_j$。此时，计算前向微分的每一趟都是先初始化一个独热向量，其中只有${\dot{x}}_i=1$，其它都是0。对给定输入$\mathbf{x}=\mathbf{a}$，代码计算
$${{\dot{y}}_j=\frac{\partial y_j}{\partial x_i}|}_{\mathbf{x}=\mathbf{a}},j=1,\dots ,m$$
这样会得到雅可比矩阵
$${\mathbf{J}}_f={\left[\begin{array}{ccc}\frac{\partial y_1}{\partial x_1}& \cdots & \frac{\partial y_1}{\partial x_n}\\ ⋮& \ddots & ⋮\\ \frac{\partial y_m}{\partial x_1}& \cdots & \frac{\partial y_m}{\partial x_n}\end{array}\right]|}_{{}_{\mathbf{x}=\mathbf{a}}}$$
的一列，因此对$n$维变量需要计算$n$次

前向模式计算自动微分的好处是给出了一种简便的方法来计算雅可比-向量乘积
$${\mathbf{J}}_f\mathbf{r}=\left[\begin{array}{ccc}\frac{\partial y_1}{\partial x_1}& \cdots & \frac{\partial y_1}{\partial x_n}\\ ⋮& \ddots & ⋮\\ \frac{\partial y_m}{\partial x_1}& \cdots & \frac{\partial y_m}{\partial x_n}\end{array}\right]\left[\begin{array}{c}{r}_1\\ ⋮\\ r_n\end{array}\right]$$
只需要设置$\dot{\mathbf{x}}=\mathbf{r}$即可，而且这种做法不牵扯额外的矩阵计算。对于比较特殊的情况$f:{\mathbb{R}}^n\to \mathbb{R}$，只需要设置$\dot{\mathbf{x}}=\mathbf{r}$就可以算出沿着给定向量$\mathbf{r}$的方向导数$\nabla f\cdot \mathbf{r}$

前向模式适用于输入向量维度$n$小于输出向量维度$m$的情况，但是如果$n>>m$，例如神经网络里输入向量成百万维，而最后的损失函数是一个标量，这种计算方法就太慢了（因为要迭代$n$次），需要后向模式计算

二元数

从数学角度讲，前向模式自动微分可以看做是使用二元数（dual number）对某个函数求值，而二元数可以定义为被截断的泰勒级数，形式为
$$v+\dot{v}ϵ$$
其中$v,\dot{v}\in \mathbb{R}$，$ϵ$是一个幂零数（${ϵ}^2=0,ϵ̸=0$）。根据幂零数的性质，可以得到
$$\begin{array}{rl}(v+\dot{v}ϵ)+(u+\dot{u}ϵ)& =(v+u)+(\dot{v}+\dot{u})ϵ\\ (v+\dot{v}ϵ)(u+\dot{u}ϵ)& =(vu)+(v\dot{u}+\dot{v}u)ϵ\end{array}$$
这里$ϵ$的系数可以对应到微分的加法和乘法法则。注意到对偶数的表示可以类似于实数的表示，对实数$x+yi$，计算机可以只存储$(x,y)$，而对偶数也可以只存储$(x,\dot{x})$。如果使用$⟨v,\dot{v}⟩$来代表$v+\dot{v}ϵ$，有
$$\begin{array}{rl}⟨v,\dot{v}⟩+⟨u,\dot{u}⟩& =⟨(v+u),(\dot{v}+\dot{u})⟩=⟨(v+u),\dot{(v+u)}⟩\\ ⟨v,\dot{v}⟩\cdot ⟨u,\dot{u}⟩& =⟨vu,\dot{v}u+v\dot{u}⟩=⟨vu,\dot{(vu)}⟩\end{array}$$
利用这一点，在$f$对$v$做泰勒展开有效的区域，
$$f(v+\dot{v}ϵ)=f(v)+f^{\prime }(v)\dot{v}ϵ$$
也就是
$$f(⟨v,\dot{v}⟩)=⟨f(v)+\dot{(f(v))}⟩$$
使用二元数做数据结构就能同时得到原值和导数值（此时泰勒展开的部分可以看做是一个二维空间，基分别是1和$ϵ$，系数是$v$和$\dot{v}$——感谢sakigami_yang的总结）

上述结论对链式法则也适用：连续使用两次上式结论，有
$$\begin{array}{rl}f(g(v+\dot{v}ϵ))& =f(g(v)+g^{\prime }(v)\dot{v}ϵ)\\ & =f(g(v))+f^{\prime }(g(v))g^{\prime }(v)\dot{v}ϵ\end{array}$$
此时$ϵ$的系数就是$f$和$g$组合的导数，因此只要使基本操作满足不变性$f(v+\dot{v}ϵ)=f(v)+f^{\prime }(v)\dot{v}ϵ$，那么它们的组合也会满足。这意味着将任何数$v$记为$v+0ϵ$，并在求值时令$ϵ$的系数为1，就可以得到函数的导数
$${\frac{df(x)}{dx}|}_{x=v}=\mathrm{e}\mathrm{p}\mathrm{s}\mathrm{i}\mathrm{l}\mathrm{o}{\mathrm{n}}^{\prime }\mathrm{s}\text{-}\mathrm{c}\mathrm{o}\mathrm{e}\mathrm{f}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{t}(\mathrm{d}\mathrm{u}\mathrm{a}\mathrm{l}\text{-}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}(f)(v+1ϵ))$$
这个结论可以扩展到任意程序结构，不只局限于函数$f$，因为二元数作为一个数据类型可以包含在任意其它数据结构中。对数据结构中的任意一个二元数，只要不对其做算术操作，它就不会变；如果做了操作，微分也会随之改变

实践中，使用某种语言实现的$f$会被送进某个自动微分工具，工具会自动对其增强，加入额外代码以处理二元操作，因此可以同时计算函数和函数的导数。具体实现可能是自动修改代码或进行运算符重载，因此这个增强操作是对用户透明的

后向模式（Backward mode）

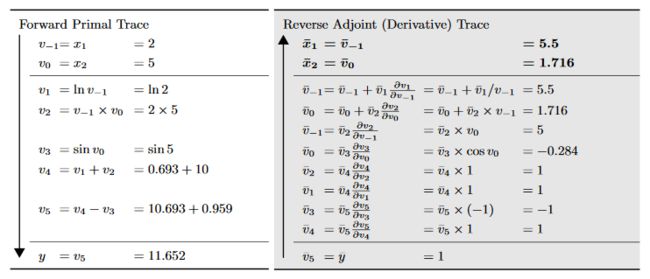
后向模式的自动微分对应于一种更泛化的反向传播算法，其从一个给定的输出开始向后传播导数。具体做法是对每个中间值$v_i$计算一个伴随值
$${\bar{v}}_i=\frac{\partial y_j}{\partial v_i}$$
代表了输出$y_j$对$v_i$变化量的敏感度。在反向传播中，$y$通常是一个标量，对应误差$E$

后向模式的自动微分计算过程分为两个阶段：

• 第一个阶段是前向计算原始函数中的每个中间值$v_i$，记录计算图中的依赖关系
• 第二个阶段是后向传播伴随值${\bar{v}}_i$，计算导数

仍以前图计算过程为例，假设需要计算${\bar{v}}_0$，从图中可以看到它是通过产生$v_2$和$v_3$来影响$y$，根据全微分定理，它对$y$变化量的贡献可以如下计算
$$\frac{\partial y}{\partial v_0}=\frac{\partial y}{\partial v_2}\frac{\partial v_2}{\partial v_0}+\frac{\partial y}{\partial v_3}\frac{\partial v_3}{\partial v_0}$$
或者引入前面${\bar{v}}_i$的记法，上式也可以写为
$${\bar{v}}_0={\bar{v}}_2\frac{\partial v_2}{\partial v_0}+{\bar{v}}_3\frac{\partial v_3}{\partial v_0}$$
计算梯度时则可以采用如下更新方式
$$\begin{array}{rl}{\bar{v}}_0& ={\bar{v}}_3\frac{\partial v_3}{\partial v_0}\\ {\bar{v}}_0& ={\bar{v}}_0+{\bar{v}}_2\frac{\partial v_2}{\partial v_0}\end{array}$$
所有变量的更新方式如下图所示

后向模式的最大优势是对于诸如$f:{\mathbb{R}}^n\to \mathbb{R}$这样的函数，一次后向模式就可以得到全部梯度$\nabla f$。由于机器学习问题大部分都是要求标量目标函数对高维参数的梯度，因此在这样的场景下后向模式的效率比前向模式的效率要高很多

与前向模式类似，后向模式通过设置$\bar{\mathbf{y}}=\mathbf{r}$来计算雅可比矩阵转置与向量的乘积
$${\mathbf{J}}_f^{\mathsf{T}}\mathbf{r}=\left[\begin{array}{ccc}\frac{\partial y_1}{\partial x_1}& \cdots & \frac{\partial y_m}{\partial x_1}\\ ⋮& \ddots & ⋮\\ \frac{\partial y_1}{\partial x_n}& \cdots & \frac{\partial y_m}{\partial x_n}\end{array}\right]\left[\begin{array}{c}{r}_1\\ ⋮\\ r_n\end{array}\right]$$
后向模式自动微分的代价是在计算过程中所需存储空间与函数操作数的数量成正比，而如何减少存储空间的利用也是学界研究的一个方向

自动微分与机器学习

基于梯度的优化

基于梯度的优化是机器学习的基石之一，问题形式是对目标函数$f:{\mathbb{R}}^n\to \mathbb{R}$通过更新参数$\Delta \mathbf{w}=-\eta \nabla f$求解极小值${\mathbf{w}}^{\ast }=\mathrm{a}\mathrm{r}\mathrm{g}{\min }_{\mathbf{w}}f(\mathbf{w})$，基本思想是当沿着梯度的反方向移动时，目标函数$f$的值减小得最快。可以看出对于比较大的$n$，后向模式的自动微分提供了非常有效的计算梯度的方法。一些基于牛顿法的二阶方法会使用梯度$\nabla f$和Hessian矩阵${\mathbf{H}}_f$，此时参数的更新方式是$\Delta \mathbf{w}=-\eta {\mathbf{H}}_f^{-1}\nabla f$，这种方法收敛更快，但是计算量会变大，因此通常会使用Hessian矩阵的数值逼近，即诸如BFGS和L-BFGS这样的拟牛顿法。有时可能不需要计算完整的Hessian矩阵，只需要计算Hessian矩阵与向量的内积，这时就可以将自动微分的前向计算和后向计算综合利用：对函数$f:{\mathbb{R}}^n\to \mathbb{R}$，假设要求$\mathbf{x}$处的值，向量为$\mathbf{v}$，那么首先设置$\dot{\mathbf{x}}=\mathbf{v}$，利用前向模式计算方向导数$\nabla f\cdot \mathbf{v}$，然后对结果使用后向模式，就可以得到${\nabla }^{2}f\cdot \mathbf{v}={\mathbf{H}}_f\mathbf{v}$。一些比较成熟的自动微分库会对大规模机器学习问题做更复杂的优化

神经网络、深度学习与可微分编程

训练神经网络的基本方法是反向传播算法，而反向传播算法只是自动微分的一种特殊情况而已，其基本过程就是利用自动微分的后向模式计算目标函数对参数的梯度。时下流行的深度学习框架都会提供自动计算微分的方法，不过底层机制通常都会混用诸如“autodiff”、“自动微分”和“符号微分”等术语。主流的深度学习框架分为两个流派

• Theano、TensorFlow、Caffe和CNTK都使用了静态计算图。开发者需要首先构建一个计算图模型，然后框架在执行时解释这个模型。这种做法的优点是框架可以对图做出优化，但是控制流会显得不直观，难以调试。“静态”的意思是图的结构不会随输入的变化和改变
• Autograd、Chainer和PyTorch都使用了真正的、通用的后向自动微分算法，因此不需要额外的解释器，可以随意编写控制流相关的代码，调试起来更简单，程序也更直观。“动态”的意思是图的结构在运行时构建，而且在每个迭代都可能变化

可微分编程是另一个新出现的名词，其背景是一些人认识到对某个问题来说，深度学习模型本质上是可能解决方案的可微程序模板，这些模板的表现形式是可微的有向图，由各种功能块组成。模板的参数是通过对任务相关的目标函数做基于梯度的优化学习得出。在此范式下，神经网络本质上就是一类参数化的可微程序，由一些代码块组成（例如前馈元素、卷积元素、循环元素等），而这些代码块又是由算法结构拼接而成。以此为基础，研究人员又提出了一些新的可微分体系结构，例如神经图灵机以及其它可微数据结构，而通用的自动微分可以极大简化这类模型的实现

（本节后面分别介绍了自动微分在计算机视觉、NLP和概率建模中的应用，讲得比较专，而且对NLP涉及不多，就不记在这里了。当前NLP的解决方案大部分是使用深度学习，这一点在上面这一小节有所介绍。而传统的方法单独使用自动微分的不多，文章中介绍的两个方案一个是用在CRF，一个是用在HMM）

实现

陷阱

性能

由于自动微分计算过程中要记录所有产生的中间变量，因此自动微分编程框架实现时最主要的关注点是这种“记账操作”和算数过程带来的性能负载。自动微分保证计算量的增量是一个很小的常数倍数，不过如果不精心管理计算过程，会带来严重的负载问题。比如，如果使用最直接的方法为二元数分配数据结构，可能会造成频繁的内存分配/访问，这种操作在当代计算机上带来的性能代价要比单纯算数操作的代价要高。而如果使用运算符重载，也会降低效率

扰动混淆

自动微分算法在实现时还要避免出现“扰动混淆”（perturbation confusion）的bug：如果两路微分操作会影响同一块代码，那么这两路微分所引入的$ϵ$需要被区分开。当自动微分出现嵌套（计算有微分操作函数的微分）时，也要注意避免这样的问题

[Siskind2005]给出了一个扰动混淆的例子。首先引入如下记号：
$$\mathcal{D}fc={\frac{d}{dx}f(x)|}_{x=c}$$
引入之前的二元数的记法，并定义操作
$$\mathcal{E}(x+x^{\prime }ϵ)\triangleq x^{\prime }$$
因此
$$\mathcal{D}fc\triangleq \mathcal{E}(f(c+ϵ))$$
例如
$$\begin{array}{rl}{\frac{d}{dx}{x}^2+x+1|}_{x=3}& =\mathcal{D}(\lambda x.x\times x+x+1)3\\ & =\mathcal{E}((\lambda x.x\times x+x+1)(3+ϵ))\\ & =\mathcal{E}((3+ϵ)\times (3+ϵ)+(3+ϵ)+1)\\ & =\mathcal{E}(9+6ϵ+3+ϵ+1)\\ & =\mathcal{E}(13+7ϵ)\\ & =7\end{array}$$
那么使用如上记法，如何计算
$${\frac{d}{dx}\left(x\left({\frac{d}{dy}x+y|}_{y=1}\right)\right)|}_{x=1}$$
这个式子如果直接计算不难看出应该是1，但是如果使用如上的操作
$$\begin{array}{rl}& \mathcal{D}(\lambda x.x\times (\mathcal{D}(\lambda y.x+y)1))1\\ =& \mathcal{E}((\lambda x.x\times (\mathcal{D}(\lambda y.x+y)1))(1+ϵ))\\ =& \mathcal{E}((1+ϵ)\times (\mathcal{D}(\lambda y.(1+ϵ)+y)1))\\ =& \mathcal{E}((1+ϵ)\times (\mathcal{E}((\lambda y.(1+ϵ)+y)(1+ϵ))))\\ =& \mathcal{E}((1+ϵ)\times (\mathcal{E}((1+ϵ)+(1+ϵ))))\\ =& \mathcal{E}((1+ϵ)\times (\mathcal{E}(2+2ϵ)))\\ =& \mathcal{E}((1+ϵ)\times 2)\\ =& \mathcal{E}(2+2ϵ)\\ =& 2̸=1\end{array}\text{\hspace{1em}(1)}$$
为什么会出现这样的问题呢？这是因为在上面(1)式中乘数里，对$\mathcal{E}$所包含的函数，其参数中的$ϵ$是$y$的$ϵ$，而函数体中的$ϵ$是$x$的$ϵ$，两者是对$\mathcal{D}$的不同调用，不能混为一谈

数值计算的陷阱

将数学公式翻译成代码时，还要注意数值计算的问题。例如

• $\log (1+x)$应该使用log1p(x)，而不是log(1+x)。假设x = 1e-99，前者得到1e-99，后者则是0.0
• $\sqrt{x^2+y^2+z^2}$应该使用hypot(x, hypot(y, z))，因为任何一个数的平方都可能会造成上溢或下溢
• ${\tan }^{-1}(y/x)$应该使用atan2(y, x)，而不应该使用atan(y/x)，因为要考虑$x\le 0$的若干种情况

与机器学习有关的一个典型问题是，对$\log \sum \exp \{x_n\}$，需要直接使用logsumexp这样的函数来避免softmax可能的上溢/下溢情况

近似问题

如果编写一个方法，其目的只是为了逼近某个理想函数，那么这个方法的自动微分求出的是实际写出的过程的微分，而不是理想函数的微分。例如对于$e^x$，老式系统可能会使用一个麦克劳林级数做逼近
$$e^x=\sum _{n=0}^{\infty }\frac{x^n}{n!}=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots$$
对这个展开做自动微分的结果是求出每个求和项的自动微分然后再求和。尽管问题也不大，但是直接使用原式是最保险的。因此，实现自动微分时，要逼近导数，而非微分近似值

实现方法

本文最后罗列了一些实现，并且将这些实现分成了三个类别

• 基本库。实现一个库，暴露一些方法供其他函数调用。代表作是AutoDiff
• 编译器/源代码转换。可以看做是一个预处理器，将代码作为输入，输出同语言的，自动微分版的新代码。代表作是tangent
• 运算符重载。代表作是ad和autograd，chainer和PyTorch的实现也属于这一类

一些课程也提供了一些关于自动微分的作业，包括

• 华盛顿大学CSE599W（陈天奇主讲）
• CMU 10-605的讲义和作业

TensorFlow的实现

（本小节没有出现在前面所说的综述中，参考了知乎问题TensorFlow是如何求导的、StackOverflow问题Does tensorflow use automatic or symbolic gradients和TensorFlow关于eager execution模式的官方文档）

为了了解TensorFlow中自动微分的实现，需要先找到如何计算梯度。考虑到梯度常见的用处是最小化损失函数，因此可以先从损失函数如何优化的方向上探索，即从Optimizer类的minimize方法入手。这个方法调用了compute_gradients方法以获得参数的梯度（然后会调用apply_gradients以利用梯度更新参数，与本文讨论的内容暂时没有什么关系，所以先略去了）。由于TensorFlow有两种计算梯度的方法：一种是经典的静态图模式，一种是新加入的动态图模式（官方说法是eager execution模式），因此对于不同模式，compute_gradients采取了不同的实现逻辑

静态图模式

TensorFlow的经典模式是先建立一个静态图，然后这个静态图在一个会话里执行。在这种模式下，compute_gradients方法进一步调用tensorflow.python.ops.gradients_impl里的gradients方法

grads = gradients.gradients(
        loss, var_refs, grad_ys=grad_loss,
        gate_gradients=(gate_gradients == Optimizer.GATE_OP),
        aggregation_method=aggregation_method,
        colocate_gradients_with_ops=colocate_gradients_with_ops)

其中loss是计算损失值的张量，var_refs是变量列表，grad_ys存储计算出的梯度，gate_gradients是一个布尔变量，指示所有梯度是否在使用前被算出，如果设为True，可以避免竞争条件。不过gradients方法在实现上用途更广泛一些，简单说，它就是为了计算一组输出张量ys = [y0, y1, ...]对输入张量xs = [x0, x1, ...]的梯度，对每个xi有grad_i = sum[dy_j/dx_i for y_j in ys]。默认情况下，grad_loss是None，此时grad_ys被初始化为全1向量

gradients实际上直接调用内部方法_GradientsHelper

@tf_export("gradients")
def gradients(ys,
              xs,
              grad_ys=None,
              name="gradients",
              colocate_gradients_with_ops=False,
              gate_gradients=False,
              aggregation_method=None,
              stop_gradients=None):
  # Creating the gradient graph for control flow mutates Operations.
  # _mutation_lock ensures a Session.run call cannot occur between creating and
  # mutating new ops.
  with ops.get_default_graph()._mutation_lock():  # pylint: disable=protected-access
    return _GradientsHelper(ys, xs, grad_ys, name, colocate_gradients_with_ops,
                            gate_gradients, aggregation_method, stop_gradients)

这个方法会维护两个重要变量

• 一个队列queue，队列里存放计算图里所有出度为0的操作符
• 一个字典grads，字典的键是操作符本身，值是该操作符每个输出端收到的梯度列表

反向传播求梯度时，每从队列中弹出一个操作符，都会把它输出变量的梯度加起来（对应全微分定理）得到out_grads，然后获取对应的梯度计算函数grad_fn。操作符op本身和out_grads会传递给grad_fn做参数，求出输入的梯度

if grad_fn:
  # If grad_fn was found, do not use SymbolicGradient even for
  # functions.
  in_grads = _MaybeCompile(grad_scope, op, func_call,
                           lambda: grad_fn(op, *out_grads))
else:
  # For function call ops, we add a 'SymbolicGradient'
  # node to the graph to compute gradients.
  in_grads = _MaybeCompile(grad_scope, op, func_call,
                           lambda: _SymGrad(op, out_grads, xs))

（不过这里似乎说明TensorFlow是自动微分和符号微分混用的）

该操作符处理以后，会更新所有未经过处理的操作符的出度和queue（实际上就是一个拓扑排序的过程）。这样，当queue为空的时候，整个计算图处理完毕，可以得到每个参数的梯度

静态图模式下梯度计算的调用过程大致如下所示

Optimizer.minimize
|---Optimizer.compute_gradients
    |---gradients (gradients_impl.py)
        |---_GradientsHelper (gradients_impl.py)

梯度计算函数

前面提到，在_GradientsHelper函数里要调用一个grad_fn函数，该函数用来计算给定操作符的梯度。在TensorFlow里，每个计算图都可以分解到操作符（op）层级，每个操作符都会定义一个对应的梯度计算函数。例如，在python/ops/math_grad.py里定义的Log函数的梯度

@ops.RegisterGradient("Log")
def _LogGrad(op, grad):
  """Returns grad * (1/x)."""
  x = op.inputs[0]
  with ops.control_dependencies([grad]):
    x = math_ops.conj(x)
    return grad * math_ops.reciprocal(x)

返回的就是已有梯度和x倒数的积，对应于
$$\frac{df(g(x))}{dx}=\frac{df(u)}{du}\frac{du}{dx}\to f^{\prime }(\log (x))\cdot \frac{1}{x}\mathrm{i}\mathrm{f}u(x)=\log (x)$$
注意每个函数都使用了装饰器RegisterGradient包装，对有m个输入，n个输出的操作符，相应的梯度函数需要传入两个参数

• 操作符本身
• n个张量对象，代表对每个输出的梯度

返回m个张量对象，代表对每个输入的梯度

大部分操作符的梯度计算方式已经由框架给出，但是也可以自定义操作和对应的梯度计算函数。假设要定义一个Sub操作，接受两个输入x和y，输出一个x-y，那么这个函数是
$$\mathrm{S}\mathrm{u}\mathrm{b}(x,y)=x-y$$
显然有
$$\frac{\partial \mathrm{S}\mathrm{u}\mathrm{b}}{\partial x}=1,\frac{\partial \mathrm{S}\mathrm{u}\mathrm{b}}{\partial y}=-1$$
那么对应的代码就是

@tf.RegisterGradient("Sub")
  def _sub_grad(unused_op, grad):
    return grad, tf.negative(grad)

动态图模式

在动态图模式下，TensorFlow不需要预先定义好完整的计算图，每个操作也可以返回具体的值，方便调试。下面给出了一个使用动态图求解线性回归的例子（改动自官方示例代码）

import tensorflow as tf
tf.enable_eager_execution()

NUM_EXAMPLES = 1000
training_inputs = tf.random_normal([NUM_EXAMPLES])
noise = tf.random_normal([NUM_EXAMPLES])
training_outputs = training_inputs * 3 + 2 + noise


def prediction(x, w, b):
    return x * w + b


# A loss function using mean-squared error
def loss(weights, biases):
    error = prediction(training_inputs, weights, biases) - training_outputs
    return tf.reduce_mean(tf.square(error))


train_steps = 200
learning_rate = 0.1
# Start with arbitrary values for W and B on the same batch of data
weight = tf.Variable(5.)
bias = tf.Variable(10.)
optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)

for i in range(20):
    print("Initial loss: {:.3f}".format(loss(weight, bias)))
    optimizer.minimize(lambda: loss(weight, bias))

print("Final loss: {:.3f}".format(loss(weight, bias)))
print("W = {}, B = {}".format(weight.numpy(), bias.numpy()))

仍然以Optimizer类的minimize方法为入口，跟进到compute_gradients方法，可以看到在动态图模式下，相关代码比较简短

if callable(loss):
  with backprop.GradientTape() as tape:
    if var_list is not None:
      tape.watch(var_list)
    loss_value = loss()

    # Scale loss if using a "mean" loss reduction and multiple towers.
    # Have to be careful to call distribute_lib.get_loss_reduction()
    # *after* loss() is evaluated, so we know what loss reduction it uses.
    # TODO(josh11b): Test that we handle weight decay in a reasonable way.
    if (distribute_lib.get_loss_reduction() ==
        variable_scope.VariableAggregation.MEAN):
      num_towers = distribution_strategy_context.get_distribution_strategy(
      ).num_towers
      if num_towers > 1:
        loss_value *= (1. / num_towers)
        
  if var_list is None:
    var_list = tape.watched_variables()
  grads = tape.gradient(loss_value, var_list, grad_loss)
  return list(zip(grads, var_list))

之前看到过一个比喻：自动微分的工作原理就像是录制一盘磁带：前向计算所有操作的时候，实际上是在录制正在进行的操作。等到录制结束，倒带播放，就得到了梯度。TensorFlow也遵循了这样的比喻，所以在动态图模式下自动微分的灵魂是一个GradientTape（“磁带”）类的对象，通过这个对象记录数据，求出梯度

在该方法的第一步里，GradientTape类对象tape会在自己的context下“观察”所有需要被记录的对象。默认情况下，使用tf.Variable 或tf.get_variable()创建的对象都是trainable的，也是会被观察的（自动放在watched_variables里）。然后，调用gradient方法来计算所有被观察对象的梯度，核心代码为

flat_grad = imperative_grad.imperative_grad(
        _default_vspace, self._tape, nest.flatten(target), flat_sources,
        output_gradients=output_gradients)

这个函数最后会调用一个C++实现的ComputeGradient函数，其伪代码大致如下

template 
// 使用了传统C的约定，返回一个状态码，结果保存在result变量里
// 核心思想还是对有向图使用拓扑排序，找到出度为0的点，聚合上游梯度，求出下游梯度
Status GradientTape::ComputeGradient(
    const VSpace& vspace,
    gtl::ArraySlice target_tensor_ids,
    gtl::ArraySlice source_tensor_ids,
    gtl::ArraySlice output_gradients,
    std::vector* result) {
  // 构建一个输入张量的集合
  gtl::FlatSet sources_set(source_tensor_ids.begin(),
                                  source_tensor_ids.end());
  // 初始化，找到所有与输出张量有关的op，计算它们的出度、引用数等
  BackpropInitialState state = PrepareBackprop(
      target_tensor_ids, tensor_tape_, &op_tape_, sources_set, persistent_);
  // 找到所有出度为0的op
  std::vector op_stack =
      InitialStack(state.op_tape, state.op_missing_tensor);
  gtl::FlatMap> gradients;
  // 将所有最终输出的输出梯度设为1
  Status s = InitialGradients(vspace, target_tensor_ids, output_gradients,
                              tensor_tape_, state.op_tape, &gradients);
  while (!op_stack.empty()) {
    获得一个op，从state.op_tape擦除之
    获取输出的梯度（上游梯度）
    计算输入的梯度（下游梯度）。大部分操作是使用CallBackwardFunction来完成
    对每个输入张量，看它是哪些op的输出张量，将该op“未计算梯度的输出张量”的计数减1。当该计数降为0时，这个op相当于出度为0，可以放入op_stack
  }
  聚合所有源向量的梯度
}

可以看出核心计算梯度的方法是调用CallBackwardFunction。这个方法调用了操作符对应的反向传播函数backward_function，而操作符和反向传播函数的对应关系会在“录制磁带”时记录

（这里有一个疑点，怀疑TensorFlow是如下逻辑：

• 若某op有自己的grad_op，那么在导入包时就会建立联系（参见前面静态图模式下对“梯度计算函数”的定义）
• 有一些函数会用户自己定义对应的梯度实现，这个对应关系在“录制磁带”时记录

只是猜想，不是很确定，欢迎证明/证伪）

动态计算图下梯度计算的调用过程大致如下所示

Optimizer.minimize
|---Optimizer.compute_gradients
    |---GradientTape.gradient
        |---imperative_grad
            |---TFE_Py_TapeGradient (python/eager/pywrap_tfe_src.cc)
                |---GradientTape<>::ComputeGradient (c/eager/tape.h)