神经翻译笔记3扩展e第1部分. Word2Vec原理及若干关于词向量的扩展知识

神经翻译笔记3扩展e第1部分. Word2Vec原理及若干关于词向量的扩展知识

本文共分为三节，由若干文章拼接而成。第一节具体推导word2vec参数的更新规则，第二节介绍在词表比较大时对softmax做近似的方法，第三部分介绍如何生成好的词向量

Word2vec的参数学习

本节内容完全来自于[Rong2014]

连续词袋模型（CBOW）

上下文仅有一个单词的情况

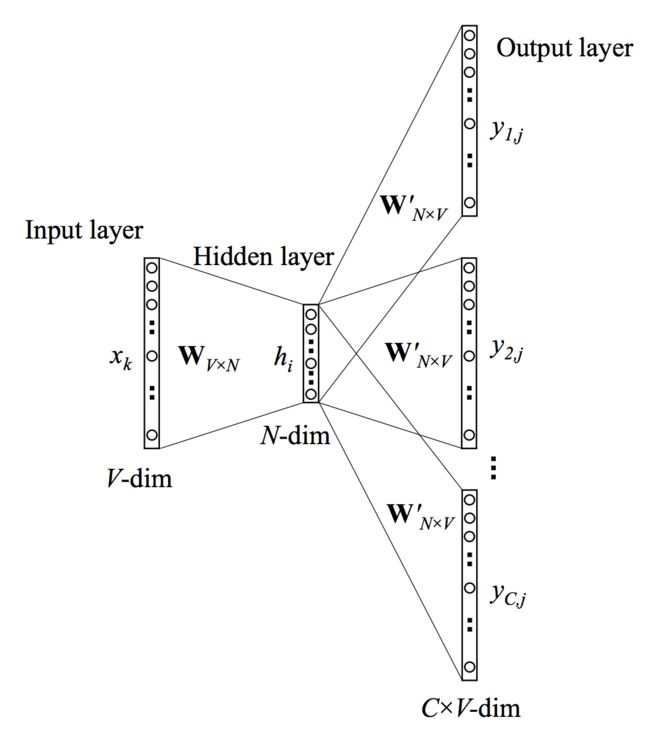
上下文只有一个单词时，网络做的事情其实类似于二元语法模型。假设词表大小为$V$，隐藏层大小为$N$，输入层到隐藏层及隐藏层到输出层都是全连接，输入为独热编码向量，那么网络的示意图如下图所示

从图中可知，输入层和隐藏层之间的权重可以使用$V\times N$的矩阵$\mathbf{W}$表示。假设输入的语境单词为词表中的第$k$个单词，则输入向量$\mathbf{x}$满足$x_k=1$且$\forall k^{\prime }̸=k\to x_{k^{\prime }}=0$，因此有
$$\mathbf{h}={\mathbf{W}}^{\mathsf{T}}\mathbf{x}={\mathbf{w}}_{(k,\cdot )}^{\mathsf{T}}:={\mathbf{v}}_{w_I}^{\mathsf{T}}$$
即$\mathbf{W}$的第k行行向量实际上就是词表中第k个单词词向量的转置，记输入单词词向量为${\mathbf{v}}_{w_I}$

假设最后得到的得分向量为$\mathbf{u}$，则从隐藏层到输出层有
$$\mathbf{u}={\mathbf{W}}^{\prime \mathsf{T}}\mathbf{h}\text{\hspace{1em}(1)}$$
其中$\mathbf{u}$的第$j$行元素$u_j$为
$$u_j={\mathbf{w}}_{(\cdot ,j)}^{\prime \mathsf{T}}\mathbf{h}\text{\hspace{1em}(2)}$$
这里${\mathbf{w}}_{(\cdot ,j)}^{\prime }$是${\mathbf{W}}^{\prime }$的第$j$列。记${\mathbf{w}}_{(\cdot ,j)}^{\prime }$为${\mathbf{v}}_{w_O}^{\prime }$

得到$\mathbf{u}$以后，可以使用softmax来得到单词的后验分布：给定上文单词为$w_I$的情况下，出现单词$w_O$的概率为
$$P(w_O|w_I)=y_j=\frac{\exp (u_j)}{{\sum }_{j^{\prime }=1}^V\exp (u_{j^{\prime }})}\text{\hspace{1em}(3)}$$
将式(1)和(2)代入(3)可得
$$P(w_O|w_I)=\frac{\exp \left({\mathbf{v}}_{w_O}^{\prime \mathsf{T}}{\mathbf{v}}_{w_I}\right)}{{\sum }_{j^{\prime }=1}^V\exp \left({\mathbf{v}}_{w_j^{\prime }}^{\prime \mathsf{T}}{\mathbf{v}}_{w_I}\right)}\text{\hspace{1em}(4)}$$

可见对同一个单词$w$来说，会有两个嵌入表示${\mathbf{v}}_w$和${\mathbf{v}}_w^{\prime }$，前者是$\mathbf{W}$的第$i$行行向量，后者是${\mathbf{W}}^{\prime }$的第$i$列列向量。在后续的分析中，称前者为单词$w$的输入向量，后者为单词$w$的输出向量

隐藏层到输出层权重的更新

假设给定单词$w_k$，期望输出是单词$w_{j^{\ast }}$，那么模型优化的目标是要最大化正确单词对应的概率$y_{j^{\ast }}$，有
$$\begin{array}{rl}{\mathrm{argmax}}_{{\mathbf{W}}^{\prime }}p(w_O|w_I)& ={\mathrm{argmax}}_{{\mathbf{W}}^{\prime }}{y}_{j^{\ast }}\\ & ={\mathrm{argmax}}_{{\mathbf{W}}^{\prime }}\log y_{j^{\ast }}\\ & ={\mathrm{argmax}}_{{\mathbf{W}}^{\prime }}\left(u_{j^{\ast }}-\log \sum _{j^{\prime }=1}^V\exp (u_{j^{\prime }})\right)\end{array}$$
记$E=-\log p(w_O|w_I)$ 为学习的目标函数，那么学习的目的就是最小化$E$。可知
$$\frac{\partial E}{\partial u_j}=y_j-t_j:=e_j$$
其中$t_j=1(j=j^{\ast })$。或者可以写为
$$\frac{\partial E}{\partial u_j}=\{\begin{array}{ll}{y}_j-1& j=j^{\ast }\\ y_j& \mathrm{e}\mathrm{l}\mathrm{s}\mathrm{e}\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\end{array}$$
接着可以求出$E$对${\mathbf{W}}^{\prime }$中每个元素$w_{ij}^{\prime }$的偏导数
$$\frac{\partial E}{\partial w_{ij}^{\prime }}=\frac{\partial E}{\partial u_j}\cdot \frac{\partial u_j}{\partial w_{ij}^{\prime }}=e_j\cdot h_i$$
因此梯度下降的更新方法为
$$w_{ij}^{\prime (\mathrm{n}\mathrm{e}\mathrm{w})}=w_{ij}^{\prime (\mathrm{o}\mathrm{l}\mathrm{d})}-\eta \cdot e_j\cdot h_i$$
向量化的形式为
$${\mathbf{v}}_{w_j}^{\prime (\mathrm{n}\mathrm{e}\mathrm{w})}={\mathbf{v}}_{w_j}^{\prime (\mathrm{o}\mathrm{l}\mathrm{d})}-\eta \cdot e_j\cdot \mathbf{h}$$
这意味着，当$y_j>t_j$时，$e_j$为正值，${\mathbf{v}}_{w_j}^{\prime }$会变小。由于$t_j$只能为0或1，因此这说明给定输入单词为$w_I$时，对不是期望单词序号$j^{\ast }$的$j$，$w_j$的输出向量会变小，反之相反

输入层到隐藏层权重的更新

首先计算目标函数$E$对隐藏层每个输出元素$h_i$的偏导数。由于隐藏层到输出层是全连接的，因此$h_i$对每个$u_j$都有贡献，使用全微分公式有
$$\frac{\partial E}{\partial h_i}=\sum _{j=1}^V\frac{\partial E}{\partial u_j}\cdot \frac{\partial u_j}{\partial h_i}=\sum _{j=1}^V{e}_j\cdot w_{ij}^{\prime }:=e_i^{\prime }$$
其中$e_i^{\prime }$是$N$维向量${\mathbf{e}}^{\prime }$的第$i$个元素。由于输入层到隐藏层也是一个全连接，因此有
$$h_i=\sum _{k=1}^V{x}_k\cdot w_{ki}$$
所以对$\mathbf{W}$的每个元素$w_{ki}$，有
$$\frac{\partial E}{\partial w_{ki}}=\frac{\partial E}{\partial h_i}\cdot \frac{\partial h_i}{\partial w_{ki}}=e_i^{\prime }\cdot x_k$$
写成向量（矩阵）形式，为
$$\frac{\partial E}{\partial \mathbf{W}}=\mathbf{x}\otimes {\mathbf{e}}^{\prime }=\mathbf{x}{\mathbf{e}}^{\prime \mathsf{T}}$$
由于$\mathbf{x}$是独热向量，因此$\partial E/\partial \mathbf{W}={\mathbf{e}}^{\prime \mathsf{T}}$，即
$${\mathbf{v}}_{w_I}^{(\mathrm{n}\mathrm{e}\mathrm{w})}={\mathbf{v}}_{w_I}^{(\mathrm{o}\mathrm{l}\mathrm{d})}-\eta {\mathbf{e}}^{\prime \mathsf{T}}$$
这意味着本次更新只有输入单词对应的那一行参数会受到影响

从前面的推导中可以看出，${\mathbf{e}}^{\prime }$实际上是$V$个输出向量${\mathbf{v}}_j^{\prime }$的加权求和，权重是每个单词$j$的损失值$e_j=y_j-t_j$。因此如果在输出层中，单词$w_j$成为输出单词的概率被高估了，梯度下降会把输入向量$w_I$拉得离$w_j$的输出向量远一些，反之相反

综上所述，整个参数更新的过程实际上就是输出词的输出向量被输入词（邻居）的输入向量来回拉扯的过程，对输入词的输入向量也是如此。两个词的共现次数越多，对应向量之间的拉力就越强，最后整个系统在经历足够多的迭代以后，会稳定下来

上下文有多个单词的情况

当上下文有多个单词时（假设有$C$个），隐藏层会对输入向量做平均
$$\begin{array}{rl}\mathbf{h}& =\frac{1}{C}{\mathbf{W}}^{\mathsf{T}}({\mathbf{x}}_1+{\mathbf{x}}_2+\cdots +{\mathbf{x}}_C)\\ & =\frac{1}{C}({\mathbf{v}}_{w_1}+{\mathbf{v}}_{w_2}+\cdots +{\mathbf{v}}_{w_C}{)}^{\mathsf{T}}\end{array}$$
模型的损失函数并没有变化，结构变为如下形式

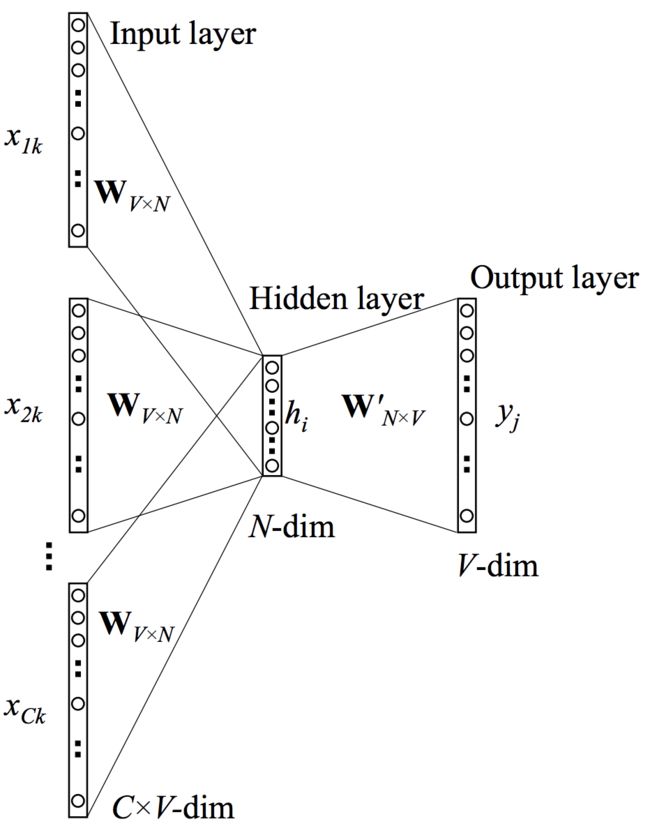
输出向量的更新方法也没有变化，唯一变化是输入向量的更新量是之前的$C$分之一
$${\mathbf{v}}_{w_{I,c}}^{(\mathrm{n}\mathrm{e}\mathrm{w})}={\mathbf{v}}_{w_{I,c}}^{(\mathrm{o}\mathrm{l}\mathrm{d})}-\frac{1}{C}\cdot \eta {\mathbf{e}}^{\prime \mathsf{T}}$$

SkipGram模型

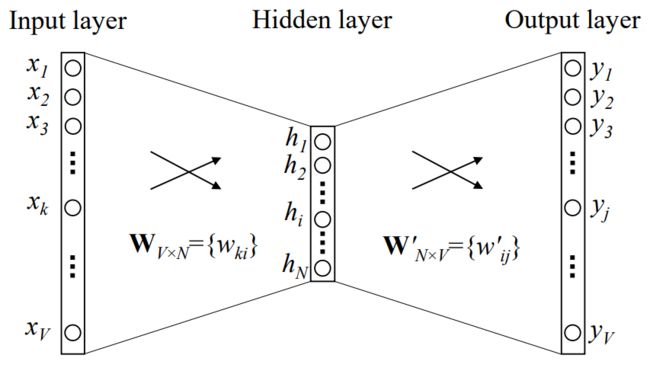
CBOW模型是用多个词做上下文，预测的是中心词；而跳表模型是用一个词做上下文，预测的是周围词。因此，对跳表模型，隐藏层输入向量与单个单词做上下文的CBOW模型没有区别
$$\mathbf{h}={\mathbf{w}}_{(k,\cdot )}^{\mathsf{T}}:={\mathbf{v}}_{w_I}^{\mathsf{T}}$$
由于是预测周围$C$个词，因此输出层要输出$C$个多项分布，输出之间共享隐藏层到输出层的矩阵${\mathbf{W}}^{\prime }$。有

$$p(w_{c,j}=w_{O,c}|w_I)=y_{c,j}=\frac{\exp (u_{c,j})}{{\sum }_{j^{\prime }=1}^V\exp (u_{j^{\prime }})}$$
其中$w_{c,j}$是输出层中第$c$个位置上的第$j$个单词，$w_{O,c}$是输出单词序列中的第$c$个单词（第$c$个位置上的实际单词），$w_I$是唯一的那个输入单词，$y_{c,j}$是模型算出第$c$个位置上是第$j$个单词的概率。由于输出层各个位置共享权重，因此
$$u_{c,j}=u_j={\mathbf{v}}_{w_j}^{\prime \mathsf{T}}\cdot \mathbf{h},\mathrm{f}\mathrm{o}\mathrm{r}c=1,2,\cdots ,C$$
其中${\mathbf{v}}_{w_j}^{\prime }$仍然是第$j$个单词的输出向量，也是${\mathbf{W}}_j^{\prime }$的第$j$列。跳表模型的示意图如下

由于是预测多个输出单词，因此需要对$C$个输出概率连乘。损失函数变为
$$\begin{array}{rl}E& =-\log p(w_{O,1},w_{O,2},\cdots ,w_{O,C}|w_I)\\ & =-\log \prod _{c=1}^C\frac{\exp (u_{c,j_c^{\ast }})}{{\sum }_{j^{\prime }=1}^V\exp (u_{j^{\prime }})}\\ & =-\sum _{c=1}^C{u}_{j_c^{\ast }}+C\cdot \log \sum _{j^{\prime }=1}^V\exp (u_{j^{\prime }})\end{array}$$
对输出的每个位置$c$，$\partial E/\partial u_{c,j}$的计算方法与之前差别不大
$$\frac{\partial E}{\partial u_{c,j}}=y_{c,j}-t_{c,j}:=e_{c,j}$$
定义$e_j$为每个位置$c$上模型都预测为$w_j$时，模型的损失值总和
$$e_j=\sum _{c=1}^C{e}_{c,j}$$
这样，跳表模型的$\partial E/\partial w_{ij}^{\prime }$、$e_i^{\prime }$和权重更新公式就和前面单个上下文CBOW模型的公式形式一样了

优化计算效率

前面提到无论是CBOW还是SkipGram算法，对每个单词都会计算出一个输入向量${\mathbf{v}}_w$和一个输出向量${\mathbf{v}}_w^{\prime }$。为了计算输出向量，对每条训练数据都要迭代词表中的每个单词$w_j$，计算原始得分$u_j$、概率$p_j$（对SkipGram是$p_{c,j}$）、误差$e_j$然后才能更新${\mathbf{v}}_j^{\prime }$。这些计算代价太高，因此对大型训练语料或者大词表使用原始做法比较难，因此人们想出了分层softmax和负采样两种做法

分层softmax

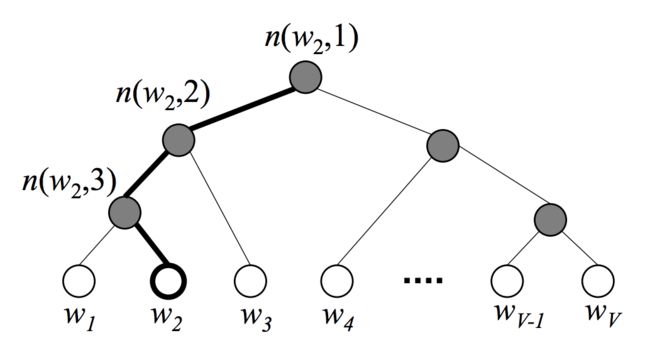
分层softmax的做法是建立一棵二叉树（更确切地说，为了快速训练，是一颗Huffman树）表达此表中的所有单词，其中所有单词对应的节点都是叶子节点，因此树一共有$V$个叶子节点，相应地有$V-1$个内部节点。而且由树的性质，从树根到每个单词的路径是唯一的，这条路径也就可以用来估计叶子节点对应单词的概率。对单词$w$，记从根节点到其对应叶子节点路径上的第$j$个节点为$n(w,j)$

在该模型中，单词不再有对应的输出向量表示，而是每个内部节点都有一个输出向量${\mathbf{v}}_{n(w,j)}^{\prime }$。令$L(w)$是路径的长度（即路径上有几个节点，因此$n(w,1)=\mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t}$，$n(w,L(w))=w$）。对所有内部节点$n$，令$\mathrm{c}\mathrm{h}(n)$为其左孩子（Mikolov的原始论文里其实无此限制），并令$[[x]]$在$x$为真时为1否则为-1，$\sigma (x)$是sigmoid函数，则一个单词是输出单词的概率是
$$p(w=w_O)=\prod _{j=1}^{L(w)-1}\sigma \left([[n(w,j+1)=\mathrm{c}\mathrm{h}(n(w,j))]]\cdot {{\mathbf{v}}_{n(w,j)}^{\prime }}^{\mathsf{T}}\mathbf{h}\right)$$

上图给出了分层softmax的一个示例。假设要计算输出单词为$w_2$的概率，这实际上是计算从根开始随机游走，有多大概率会走到$w_2$对应的叶子节点。我们先定义在每个内部节点向左走的概率为
$$p(n,\mathrm{l}\mathrm{e}\mathrm{f}\mathrm{t})=\sigma \left({\mathbf{v}}_n^{\prime \mathsf{T}}\cdot \mathbf{h}\right)$$
由于二叉树是Huffman树，每个内部节点有且仅有两个分支，因此显然$p(n,\mathrm{r}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t})=1-p(n,\mathrm{l}\mathrm{e}\mathrm{f}\mathrm{t})$。由sigmoid函数的性质，有
$$p(n,\mathrm{r}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t})=\sigma \left(-{\mathbf{v}}_n^{\prime \mathsf{T}}\cdot \mathbf{h}\right)$$
所以有
$$\begin{array}{rl}p(w_2=w_O)& =p(n(w_2,1),\mathrm{l}\mathrm{e}\mathrm{f}\mathrm{t})\cdot p(n(w_2,2),\mathrm{l}\mathrm{e}\mathrm{f}\mathrm{t})\cdot p(n(w_2,3),\mathrm{r}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t})\\ & =\sigma \left({\mathbf{v}}_{n(w_2,1)}^{\prime \mathsf{T}}\cdot \mathbf{h}\right)\cdot \sigma \left({\mathbf{v}}_{n(w_2,2)}^{\prime \mathsf{T}}\cdot \mathbf{h}\right)\cdot \sigma \left(-{\mathbf{v}}_{n(w_2,3)}^{\prime \mathsf{T}}\cdot \mathbf{h}\right)\end{array}$$
显然有
$$\sum _{i=1}^{V}p(w_i=w_O)=1$$
接下来来看一下分层softmax算法如何更新权重。为了简单起见，不失准确性地，可以记
$$\begin{array}{rl}[[\cdot ]]& :=[[n(w,j+1)=\mathrm{c}\mathrm{h}(n(w,j))]]\\ {\mathbf{v}}_j^{\prime }& :={\mathbf{v}}_{n_{(w,j)}}^{\prime }\end{array}$$

因此损失函数为
$$E=-\log p(w=w_O|w_I)=-\sum _{j=1}^{L(w)-1}\log \sigma \left([[\cdot ]]{\mathbf{v}}_j^{\prime \mathsf{T}}\mathbf{h}\right)$$

先计算$\partial E/\partial {\mathbf{v}}_j^{\prime \mathsf{T}}\mathbf{h}$。考虑到${\sigma }^{\prime }(x)=\sigma (x)(1-\sigma (x))$和$\sigma (-x)=1-\sigma (x)$，有
$$\begin{array}{rl}\frac{\partial E}{\partial {\mathbf{v}}_j^{\prime \mathsf{T}}\mathbf{h}}& =\left(\sigma \left([[\cdot ]]{\mathbf{v}}_j^{\prime \mathsf{T}}\mathbf{h}\right)-1\right)[[\cdot ]]\\ & =\{\begin{array}{ll}\sigma \left({\mathbf{v}}_j^{\prime \mathsf{T}}\mathbf{h}\right)-1& ([[\cdot ]]=1)\\ \sigma \left({\mathbf{v}}_j^{\prime \mathsf{T}}\mathbf{h}\right)& ([[\cdot ]]=-1)\end{array}\\ & =\sigma \left({\mathbf{v}}_j^{\prime \mathsf{T}}\mathbf{h}\right)-t_j\end{array}$$
其中
$$\begin{array}{r}{t}_j=\{\begin{array}{ll}1& \mathrm{i}\mathrm{f}[[\cdot ]]=1\\ 0& \mathrm{e}\mathrm{l}\mathrm{s}\mathrm{e}\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\end{array}\end{array}$$

有了$\partial E/\partial {\mathbf{v}}_j^{\prime \mathsf{T}}\mathbf{h}$以后，计算$\partial E/\partial {\mathbf{v}}^{\prime }$就容易许多：
$$\frac{\partial E}{\partial {\mathbf{v}}_j^{\prime }}=\frac{\partial E}{\partial {\mathbf{v}}_j^{\prime \mathsf{T}}\mathbf{h}}\cdot \frac{\partial {\mathbf{v}}_j^{\prime \mathsf{T}}\mathbf{h}}{\partial {\mathbf{v}}_j^{\prime }}=\left(\sigma ({\mathbf{v}}_j^{\prime \mathsf{T}}\mathbf{h})-t_j\right)\cdot \mathbf{h}$$
所以对$j=1,2,\cdots ,L(w)-1$，有内部节点输出向量的更新公式
$${\mathbf{v}}_j^{\prime (\mathrm{n}\mathrm{e}\mathrm{w})}={\mathbf{v}}_j^{\prime (\mathrm{o}\mathrm{l}\mathrm{d})}-\eta \left(\sigma ({\mathbf{v}}_j^{\prime \mathsf{T}}\mathbf{h})-t_j\right)\cdot \mathbf{h}$$

该公式对CBOW和skip-gram模型都适用。对于后者，需要对$C$个输出单词重复走一遍这个过程

为了学习输入层到隐藏层的权重，需要计算$\partial E/\partial \mathbf{h}$：
$$\begin{array}{rl}\frac{\partial E}{\partial \mathbf{h}}& =\sum _{j=1}^{L(w)-1}\frac{\partial E}{\partial {\mathbf{v}}_j^{\prime \mathsf{T}}\mathbf{h}}\cdot \frac{\partial {\mathbf{v}}_j^{\prime \mathsf{T}}\mathbf{h}}{\partial \mathbf{h}}\\ & =\sum _{j=1}^{L(w)-1}\left(\sigma ({\mathbf{v}}_j^{\prime \mathsf{T}}\mathbf{h})-t_j\right)\cdot {\mathbf{v}}_j^{\prime }\\ & :={\mathbf{e}}^{\prime }\end{array}$$

就可以继续用之前推导过的公式来更新权重

可以看出，使用分层softmax以后，参数数量没有变化（$V-1$个输出向量，$V$个输入向量），但是每个训练单词的计算复杂度从$O(V)$削减到了$O(\log (V))$

负采样

负采样的思想是，由于每次迭代要花时间更新太多输出向量，不如采样少量几个单词，把它们当做负样本。采样负样本只需要设计一个合理的概率分布就可以，这里称其为“噪声分布”，记为$P_n(w)$。原文的噪声分布参见词向量的介绍。目标函数为
$$E=-\log \sigma ({\mathbf{v}}_{w_O}^{\prime \mathsf{T}}\mathbf{h})-\sum _{w_j\in {\mathcal{W}}_{\mathrm{n}\mathrm{e}\mathrm{g}}}\log \sigma (-{\mathbf{v}}_{w_j}^{\prime \mathsf{T}}\mathbf{h})$$
其中

• $w_O$是输出单词（正样本）
• ${\mathbf{v}}_{w_O}^{\prime }$是正样本的输出向量
• 对CBOW模型，$\mathbf{h}$为$\frac{1}{C}{\sum }_{c=1}^C{\mathbf{v}}_{w_c}$；对skip-gram模型，$\mathbf{h}={\mathbf{v}}_{w_I}$
• ${\mathcal{W}}_{\mathrm{n}\mathrm{e}\mathrm{g}}=\{w_j|j=1,\cdots ,K\}$是使用分布$P_n(w)$获得的一些单词（负样本）

类似地，可以先计算出损失函数对原始得分的偏导数
$$\begin{array}{rl}\frac{\partial E}{\partial {\mathbf{v}}_{w_j}^{\prime \mathsf{T}}\mathbf{h}}& =\{\begin{array}{ll}\sigma \left({\mathbf{v}}_{w_j}^{\prime \mathsf{T}}\mathbf{h}\right)-1& \mathrm{i}\mathrm{f}{w}_j=w_O\\ \sigma \left({\mathbf{v}}_{w_j}^{\prime \mathsf{T}}\mathbf{h}\right)& \mathrm{i}\mathrm{f}{w}_j\in {\mathcal{W}}_{\mathrm{n}\mathrm{e}\mathrm{g}}\end{array}\\ & =\sigma \left({\mathbf{v}}_{w_j}^{\prime \mathsf{T}}\mathbf{h}\right)-t_j\end{array}$$

其中$t_j$意义明显，不再进一步解释。接下来的参数更新方式和$\partial E/\partial \mathbf{h}$的计算也与前面分层softmax部分的推导类似，不再赘述

Softmax的近似方法

本节主要来自于Ruder的博客文章[Ruder2016]

如本文和前面若干文章所讨论过的，softmax的最大问题是要对每个词都计算得分，因此当词表非常大时，算法的时间复杂度非常高。为了不让这个步骤成为影响效率的主要瓶颈，人们提出了很多种方法。其中softmax扩展法仍然保留了softmax的基本思想，不过对体系结构做出了修改；而采样法则是去掉了softmax层，通过修改损失函数做softmax的近似。word2vec的两个改进方案里，分层Softmax（以下简称HSM）属于第一种方法，而负采样属于第二种

（本节写作的初衷是，直觉上感觉TensorFlow不太好实现HSM，想看看有没有写得比较漂亮的代码，然后发现好像真的没有。接着，在OpenNMT-py，也就是OpenNMT的PyTorch版，的一个issue里，看到他们没有实现HSM的原因是PyTorch实现了一个更高效的方法，称为适应softmax（adaptive softmax，简称ASM）。因此勾起了我的好奇心，想看看有没有其它类似比较高效的，适用于大规模词表的softmax方法，于是就找到了Ruder的这篇文章。但是此文成文之时并没有介绍ASM，因此本节会同时覆盖两者，并把ASM作为重点。其它方法基本都会简略带过）

Softmax扩展法

除去HSM和ASM，[Ruder2016]还介绍了两种扩展方法

• 差分softmax（[Chen2016]，differentiated softmax，DSM）认为不同单词需要的参数数量不一样。少部分常见词可能需要很多参数来描述，而大部分罕见词其向量维度可以少一点。因此DSM使用了一个很大的稀疏矩阵，将其分为若干块。假设矩阵分为两块，那么左上角的子矩阵列数会多一些，行数少一些，用来刻画常见词；而右下角的子矩阵则是列数少，行数多，用来刻画罕见词。稀疏矩阵的右上角和左下角都是0。该方法的问题是对罕见词的建模能力比较弱
• CNN-softmax [Jozefowicz2016]对输出层也使用了一个字符级别的CNN（charCNN）。不过实验显示对拼写相近而意思差别很大的两个单词，charCNN的效果不太好。文章的对策是为每个单词加一个修正向量。这种做法的好处是对集外词比较鲁棒

本小节主要介绍的工作是FAIR在2016年发表的工作ASM[Grave2017]（2016年首发于arxiv），这项工作的最大特点是其目的是要有效利用GPU，比起普通softmax有2倍到10倍性能提升。其核心思想是将单词聚类，然后做分层softmax

假设训练时每批量数据大小为$B$，隐藏单元数量为$d$，词表大小为$k$，大小为$B\times d$的隐层矩阵与大小为$d\times k$的输出层矩阵相乘的计算时间为$g(k,B)$。实验表明，当固定$B$大小不变时，存在一个阈值$k_0$，使得$k\le k_0$时$g(k)$的时间为常量，$k>k_0$时$g(k)$与$k$呈线性关系，对$B$也存在一个类似的$B_0$。因此有
$$g(k,B)=\max (c+\lambda k_0{B}_0,c+\lambda kB)$$
即当矩阵相乘时，如果某个维度比较小，则相乘效率会降低。所以使用Huffman编码的效率不是最优的，原因是会导致每个内部结点下面只有两个叶子节点，节点数太少；或者如果某个内部节点下面的叶子节点都是罕见词，概率$p$都很小，也会导致$pB$变小，不划算

由于自然语言中存在Zipf现象（直观例子是87%的文档由20%单词覆盖），因此直观地说可以把词典$\mathcal{V}$划分成两个簇${\mathcal{V}}_{\mathrm{h}}$和${\mathcal{V}}_{\mathrm{t}}$，其中${\mathcal{V}}_{\mathrm{h}}$是分布的头部（头簇），只包含最常见的单词；${\mathcal{V}}_{\mathrm{t}}$是分布的尾部（尾簇），包含大量罕见词。划分应该满足$|{\mathcal{V}}_{\mathrm{h}}|\ll |{\mathcal{V}}_{\mathrm{t}}|$且$p_{\mathrm{h}}:={\sum }_{w\in {\mathcal{V}}_{\mathrm{h}}}{p}_i\gg p_{\mathrm{t}}:={\sum }_{w\in {\mathcal{V}}_{\mathrm{t}}}{p}_i$。如果使用short-list实现方式（根节点里包含一个列表，列表中存储头簇），且记$k_{\mathrm{h}}=|{\mathcal{V}}_{\mathrm{h}}|$，则总的计算时间为
$$C=g(k_{\mathrm{h}}+1,B)+g(k_{\mathrm{t}},p_{\mathrm{t}}B)$$
文章使用了一个投影矩阵来把尾簇的维度降低到$d/4$，因为罕见词不太容易被学习，使用高维空间比较浪费

类似的思想可以很容易扩展到多维划分的情况，此时词典$\mathcal{V}$被分为$\mathcal{V}={\mathcal{V}}_{\mathrm{h}}\cup {\mathcal{V}}_1\cup \dots \cup {\mathcal{V}}_J$，${\mathcal{V}}_i\cap {\mathcal{V}}_j=\varnothing$。此时比较好的策略是将所有词按出现频率降序排列，词频高的词分到比较小的簇，簇的大小依次增大（小簇里是词频高的词，大簇里是罕见词）。实验指出簇数在10到15达到最优，但是超过5以后模型ppl（perplexity，困惑度）变化不是很大，因此常用2到5个簇。确定簇数后，每个簇分配多少个单词就可以用动态规划求解

自适应softmax的TF实现可以参考这里

采样法

Softmax可以看做是将各个得分归一化的手段，采样法实际上是对归一化时的分母做近似，使用一些其它更容易计算的损失函数。采样法只在训练时可用，推断时仍然需要计算完整的softmax

为了说明上面加粗部分的结论，来看一下损失函数$J_{\theta }$对参数$\theta$的梯度。通常来讲，多元分类使用交叉熵作为损失函数，即
$$H(p,q)=-\sum _{x}p(x)\log q(x)$$
这里$p(x)$为真实概率分布，$q(x)$为近似的概率分布。对于使用softmax获得各单词概率的模型来说，$p(x)$就是一个独热向量，该向量中对应应该出现的单词的ID那一行元素为1，其余元素为0；$q(x)$是一个概率分布，由softmax得出。因此假设目标单词为$w$，则损失函数为
$$\begin{array}{rl}{J}_{\theta }& =-\log \frac{\exp ({\mathbf{v}}_w^{\prime \mathsf{T}}\mathbf{h})}{{\sum }_{w_i\in V}\exp ({\mathbf{v}}_{w_i}^{\prime \mathsf{T}}\mathbf{h})}\\ & =-{\mathbf{v}}_w^{\prime \mathsf{T}}\mathbf{h}+\log \sum _{w_i\in V}\exp ({\mathbf{v}}_{w_i}^{\prime \mathsf{T}}\mathbf{h})\end{array}$$
记$-{\mathbf{v}}_w^{\prime \mathsf{T}}\mathbf{h}$为$\mathcal{E}(w)$，则上式可以重写为
$$J_{\theta }=\mathcal{E}(w)+\log \sum _{w_i\in V}\exp (-\mathcal{E}(w_i))$$
求$J_{\theta }$对$\theta$的偏导，有
$$\begin{array}{rl}{\nabla }_{\theta }{J}_{\theta }& ={\nabla }_{\theta }\mathcal{E}(w)+{\nabla }_{\theta }\log \sum _{w_i\in V}\exp (-\mathcal{E}(w_i))\\ & ={\nabla }_{\theta }\mathcal{E}(w)+\frac{1}{{\sum }_{w_i\in V}\exp (-\mathcal{E}(w_i))}\sum _{w_i\in V}\exp (-\mathcal{E}(w_i)){\nabla }_{\theta }(-\mathcal{E}(w_i))\\ & ={\nabla }_{\theta }\mathcal{E}(w)+\sum _{w_i\in V}\frac{\exp (-\mathcal{E}(w_i))}{{\sum }_{w_j\in V}\exp (-\mathcal{E}(w_j))}{\nabla }_{\theta }(-\mathcal{E}(w_i))\end{array}$$
注意到求和项内部梯度的系数其实就是$w_i$的softmax概率，因此将其写作$P(w_i)$，有
$$\begin{array}{rl}{\nabla }_{\theta }{J}_{\theta }& ={\nabla }_{\theta }\mathcal{E}(w)+\sum _{w_i\in V}P(w_i){\nabla }_{\theta }(-\mathcal{E}(w_i))\\ & ={\nabla }_{\theta }\mathcal{E}(w)-\sum _{w_i\in V}P(w_i){\nabla }_{\theta }\mathcal{E}(w_i)\end{array}$$
因此梯度可以分为两部分，第一部分是增强目标单词$w$，第二部分是削弱非目标单词$w_i$。后者又可以写作
$$\sum _{w_i\in V}P(w_i){\nabla }_{\theta }\mathcal{E}(w_i)={\mathbb{E}}_{w_i\sim P}[{\nabla }_{\theta }\mathcal{E}(w_i)]$$
因此所有的抽样法实际上都是在求上项的近似值，以避免算$V$中所有单词$w_i$的概率

[Ruder2016]调研了若干种基于采样法的工作，本文主要介绍两项：重要性采样法（Importance Sampling，简称IS）和噪声对比估计（Noice Contrastive Estimation，简称NCE）。另一个重要的方法是负采样，在本系列博客中已经提到很多次，这里就不赘述了。不过需要注意的是，负采样可以看作是NCE的一个简化版本

IS

如果知道前面提到的单词分布$P$，那么就可以从该分布中抽样$m$个单词，计算近似期望（蒙特卡罗法）
$${\mathbb{E}}_{w_i\sim P}[{\nabla }_{\theta }\mathcal{E}(w_i)]\approx \frac{1}{m}\sum _{i=1}^m{\nabla }_{\theta }\mathcal{E}(w_i)$$
但是根据前面的分析，要避免计算每个单词的softmax分布，所以退而求其次，需要找到一个替代的分布$Q$，使得该分布容易获得，而且最好接近$P$。常用的分布$Q$是训练集中的单词词频。进一步，还可以用另一个近似来避免对抽样到的$w$计算$P(w)$。此时，计算$1/R\cdot r(w_i)$来避免计算$P(w_i)$，其中
$$\begin{array}{rl}r(w)& =\frac{\exp (-\mathcal{E}(w))}{Q(w)};R=\sum _{j=1}^{m}r(w_j)\end{array}$$
综上，有
$${\mathbb{E}}_{w_i\sim P}[{\nabla }_{\theta }\mathcal{E}(w_i)]\approx \frac{1}{R}\sum _{r=1}^{m}r(w_i){\nabla }_{\theta }\mathcal{E}(w_i)$$
需要注意的是，样本数越少，近似效果越差

关于IS法的详细内容，可以参考[Bengio2003a]

NCE

IS法的一个潜在风险是近似分布$Q$有可能偏离真实分布$P$，而NCE[Gutmann2010] [Mnih2012]则不再直接估计某个词的概率，而是使用了另一种损失函数做辅助。其核心思想是将目标单词从噪声中区分开，因此模型训练过程变成了求解一个二元分类问题。假设每个目标单词$w_i$的语境$c_i$由$n$个上文单词$w_{t-1},\dots ,w_{t-n+1}$组成（注意原始NCE论文没有考虑单词下文），$k$个噪声单词${\tilde{w}}_{ik}$来自于噪声分布$Q$（这里也使用一元词频），则类别$y=1$说明给定$c_i$得到$w_i$，类别$y=0$说明给定$c_i$得到${\tilde{w}}_{ik}$。损失函数为
$$J_{\theta }=-\sum _{w_i\in V}\left(\log P(y=1|w_i,c_i)+k{\mathbb{E}}_{{\tilde{w}}_{ik}\sim Q}[\log P(y=0|{\tilde{w}}_{ij},c_j)]\right)$$
使用蒙特卡洛模拟来计算期望，上式可化为
$$\begin{array}{rl}{J}_{\theta }& =-\sum _{w_i\in V}\left(\log P(y=1|w_i,c_i)+k\sum _{j=1}^k\frac{1}{k}\log P(y=0|{\tilde{w}}_{ij},c_j)\right)\\ & =-\sum _{w_i\in V}\left(\log P(y=1|w_i,c_i)+\sum _{j=1}^k\log P(y=0|{\tilde{w}}_{ij},c_j)\right)\end{array}$$
由于正确单词是从训练集的经验分布$P_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}$中取得且依赖于语境$c$，噪声来自于分布$Q$，因此给定语境$c$，取样到一个单词的概率为
$$P(y,w|c)=\frac{1}{k+1}{P}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}(w|c)+\frac{k}{k+1}Q(w)$$
若某个单词被抽中，则其为正确样本的条件概率为
$$\begin{array}{rl}P(y=1|w,c)& =\frac{\frac{1}{k+1}{P}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}(w|c)}{\frac{1}{k+1}{P}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}(w|c)+\frac{k}{k+1}Q(w)}\\ & =\frac{P_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}(w|c)}{P_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}(w|c)+kQ(w)}\end{array}$$
由于$P_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}(w|c)$为未知量，可以将其替为模型概率$P(w|c)$，而显然
$$P(w|c)=\frac{\exp ({\mathbf{v}}_w^{\prime \mathsf{T}}\mathbf{h})}{{\sum }_{w_i\in V}\exp ({\mathbf{v}}_{w_i}^{\prime \mathsf{T}}\mathbf{h})}$$
似乎又回到了原来的老问题，但是NCE直接将分母置为1！（更保守的做法是将分母设为一个可学习的参数，但是有研究发现学到的分母通常也都接近于1，而且方差不大）。这样，就可以直接说$P(w|c)=\exp ({\mathbf{v}}_w^{\prime \mathsf{T}}\mathbf{h})$，所以
$$P(y=1|w,c)=\frac{\exp ({\mathbf{v}}_w^{\prime \mathsf{T}}\mathbf{h})}{\exp ({\mathbf{v}}_w^{\prime \mathsf{T}}\mathbf{h})+kQ(w)}$$
由于要求解的是一个二分类问题，因此$P(y=0|w,c)=1-P(y=1|w,c)$。将上述结论代入$J_{\theta }$，可得到最终的NCE损失函数
$$J_{\theta }=-\sum _{w_i\in V}\left[\log \frac{\exp ({\mathbf{v}}_{w_i}^{\prime \mathsf{T}}\mathbf{h})}{\exp ({\mathbf{v}}_{w_i}^{\prime \mathsf{T}}\mathbf{h})+kQ(w_i)}+\sum _{j=1}^k\log \left(1-\frac{\exp \left({\mathbf{v}}_{{\tilde{w}}_{ij}}^{\prime \mathsf{T}}\mathbf{h}\right)}{\exp \left({\mathbf{v}}_{{\tilde{w}}_{ij}}^{\prime \mathsf{T}}\mathbf{h}\right)+kQ({\tilde{w}}_{ij})}\right)\right]$$
有理论证明，当NCE中噪声样本数量$k$变大时，NCE损失函数的梯度会逼近于softmax函数的梯度

NCE与其它采样法的关系

[Jozefowicz2016]论证了IS实际上是优化一个多类别分类问题（NCE是二分类），因此更适合于语言建模。当NCE使用的$k=|V|$且$Q$为均匀分布时（此时$kQ(w)=1$），NCE退化成负采样

（原计划在本文里还跟进Ruder词向量系列博客的第三部：On word embeddings - Part 3: The secret ingredients of word2vec，该文章讨论了一些词向量的理论解释，但是比较抽象，数学内容更多，因此暂时就不介绍了。有兴趣的可以移步上面的链接阅读原文，或者参考[Levy2015] [Levy2014]）

如何生成好的词向量

[Lai2016]讨论了一些训练词向量的细节，包括模型搭建、训练语料、参数设计等方面。文章调查的工作包括

• Neural Network Language Model (NNLM, [Bengio2003b])
• Log-Bilinear Language Model (LBL, [Mnih2007])
• C&W [Collobert2008]
• CBOW & Skip-gram [Mikolov2013]
• Order：文章提出的虚拟模型，将上下文单词词向量连接起来
• Global Vectors model (GloVe, [Pennington2014])

所有训练词向量的方法基本都依赖于一条分布式假设：出现在相似上下文的单词有相同意思。因此，文章调研的建模方法实际上都是在对目标单词$w$和上下文$c$之间的关系建模，不同模型的区别主要体现在 (1) 如何建模目标单词和上下文之间的关系 (2) 如何表示上下文。对于前者，大部分模型都是用给定上下文预测中心词（注意，从这个角度看，skipgram也可以看作是用上下文预测中心词，只不过此时“中心词”是滑动的），而C&W是建模$(c,w)$的分数。对于后者，word2vec没有考虑上下文的词序，而其它工作均将上下文单词词向量按序拼接，有的还加入了隐藏层来获取更强的建模能力

文章使用了三类共八项任务来评估词向量模型，包括

• 词向量的语义属性，使用了WordSim353数据集（判断单词相似性，代号ws）、TOEFL数据集（四个选项选择同义词，代号tfl）、类比数据集（检查词向量是否能表示woman = queen - king + man的关系，代号sem & syn）
• 将词向量作为下游任务的特征。包括
  • 使用IMDB数据集做文本分类（代号avg），此时模型特征是词向量的加权平均，权重是TF（term frequency）
  • 命名实体识别（NER）（代号ner），测试集是CoNLL03 shared task数据集
• 使用词向量初始化神经网络，包括使用CNN做情感分类（代号cnn）、使用神经网络做词性标注（代号pos）等

最后得到如下结论

• 对于模型来说，从目标单词与上下文之间关系的角度看，训练时只建模$(c,w)$分数的C&W不太容易捕捉词义相加和相减的关系，因此使用上下文预测目标单词的模型效果更好。从上下文表示的角度看，数据量小时，简单的模型效果更好（例如CBOW在训练语料单词量级为千万或亿时效果很好），但是语料量更大时，复杂的模型更好
  如果要用词向量初始化其他任务需要的网络，或者作为特征，结论是不同词向量模型影响不是很大，此时简单的模型就足够了

• 对于训练语料来说，同领域下，语料量越大，得到的词向量效果越好。不同领域下语料训练出的词向量变化会非常大，例如IMDB语料训出的词向量里，与"movie"相近的词包括了"this"、"it"等，说明在这个语料里movie这个词相当于是一个停用词
  文章做了一个比较有趣的实验：对于avg任务，使用纯IMDB语料训练词向量，加权作为特征，然后向训练词向量用的语料里逐渐加入wiki与纽约时报的语料，重新训练词向量，观察新特征对模型的影响。实验表明，混杂的语料总是不如纯净的IMDB语料，因此语料领域比语料数量影响大得多

• 训练词向量应该训练多少轮？实验表明使用训练词向量时对应的验证集意义不大，最好的选择是用一个简单的任务（例如前面介绍的tfl任务）来做验证。如果训练词向量是为了一个特定的任务，那么应该使用该任务对应的验证集来验证词向量效果，不过这个过程可能比较费时间。此外，对于NLP任务，50维的词向量就可以达到不错的效果

参考文献

[Rong2014] Rong, X. (2014). word2vec parameter learning explained. arXiv preprint arXiv:1411.2738.

[Ruder2016] Ruder, S. (2016). On Word Embeddinngs - Part 2: Approximating the Softmax

[Chen2016] Chen, W., Grangier, D., & Auli, M. (2016). Strategies for Training Large Vocabulary Neural Language Models. In Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers) (ACL2016) (Vol. 1, pp. 1975-1985).

[Jozefowicz2016] Jozefowicz, R., Vinyals, O., Schuster, M., Shazeer, N., & Wu, Y. (2016). Exploring the limits of language modeling. arXiv preprint arXiv:1602.02410.

[Grave2017] Grave, E., Joulin, A., Cissé, M., & Jégou, H. (2017, August). Efficient softmax approximation for GPUs. In Proceedings of the 34th International Conference on Machine Learning-Volume 70 (ICML 2017) (pp. 1302-1310).

[Bengio2003a] Bengio, Y., & Senécal, J. S. (2003, January). Quick Training of Probabilistic Neural Nets by Importance Sampling. In AISTATS (pp. 1-9).

[Gutmann2010] Gutmann, M., & Hyvärinen, A. (2010, March). Noise-contrastive estimation: A new estimation principle for unnormalized statistical models. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics (pp. 297-304).

[Mnih2012] Mnih, A., & Teh, Y. W. (2012). A fast and simple algorithm for training neural probabilistic language models. In Proceedings of the 29th International Conference on Machine Learning, ICML 2012 (Vol. 2, pp. 1751-1758).

[Levy2015] Levy, O., Goldberg, Y., & Dagan, I. (2015). Improving distributional similarity with lessons learned from word embeddings. Transactions of the Association for Computational Linguistics, 3, 211-225.

[Levy2014] Levy, O., & Goldberg, Y. (2014). Neural word embedding as implicit matrix factorization. In Advances in neural information processing systems, NeurIPS 2014 (pp. 2177-2185).

[Lai2016] Lai, S., Liu, K., He, S., & Zhao, J. (2016). How to generate a good word embedding. IEEE Intelligent Systems, 31(6), 5-14.

[Bengio2003b] Bengio, Y., Ducharme, R., Vincent, P., & Jauvin, C. (2003). A neural probabilistic language model. Journal of machine learning research, 3(Feb), (JMLR) (pp. 1137-1155).

[Mnih2007] Mnih, A., & Hinton, G. (2007, June). Three new graphical models for statistical language modelling. In Proceedings of the 24th international conference on Machine learning, ICML 2007 (pp. 641-648). ACM.

[Collobert2008] Collobert, R., & Weston, J. (2008, July). A unified architecture for natural language processing: Deep neural networks with multitask learning. In Proceedings of the 25th international conference on Machine learning, ICML 2008 (pp. 160-167). ACM.

[Mikolov2013] Mikolov, T., Chen, K., Corrado, G., & Dean, J. (2013). Efficient estimation of word representations in vector space. arXiv preprint arXiv:1301.3781.

[Pennington2014] Pennington, J., Socher, R., & Manning, C. (2014). Glove: Global vectors for word representation. In Proceedings of the 2014 conference on empirical methods in natural language processing ,EMNLP 2014 (pp. 1532-1543).