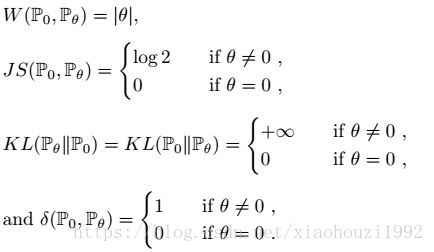Wasserstein GANs 三部曲（二）:Wasserstein GAN论文的理解

附论文地址：https://arxiv.org/abs/1701.07875

这一篇文章和下一篇讲提高WGAN的更有实际应用意义一些吧。转载请注明。

基础介绍

        学习一个概率分布，通常我们是学习这个分布的概率密度函数，假设概率密度函数存在，且由多个参数组成即，已知该分布下点集为，那么认为这些点既然出现了，就是概率最大的（相当于极大似然的思想）。问题就变成了求解使得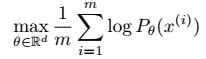。假设真实分布为，可以使用KL散度作为是否接近的标准。

        在现实生活中我们处理的分布的支撑集都是低维的，也就是说两个分布的重叠部分测度为0，可以忽略不计，那么KL散度就没有办法衡量了。

        一般的纠正办法是给模型的分布加一个有很大带宽的高斯分布，使得模型的分布覆盖所有的样本。但是，在最近的论文中提到在的时候，噪声的最佳标准方差为0.1，又图像的每一个像素值介于0到1之间，致使噪声太大，同时也降低了图像的质量，并且使用这种模型的论文中也没有用这个，所以做法不可取。

        相比估计的概率密度函数，且这个密度函数还不一定存在，可以使用另一种方法：，其中Z是一随机变量，概率密度函数为，通过改变使得分布接近于真实分布（生成器的过程）。

        在本篇论文中致力于研究测量两种分布之间距离的不同的方法，这些距离最重要的不同是对概率分布收敛的影响程度。

        分布收敛的定义：记距离或者散度为，分布序列收敛当且仅当存在一分布使得趋向于0.

        连续的定义：如果参数收敛到，那么分布就收敛到。

        分布是否收敛依赖于选择的计算距离的方法，之所以给出连续的定义，是想说如果损失函数连续，等同于连续。

论文分三部分：各种距离的比较、如何应用E-M距离、实验效果

第一部分：不同的距离定义

        

                                                假设分布是绝对连续的，且概率密度函数存在，服从同一测度

        ,        其中=

        

                                     定义为联合分布的集合，且为其边缘分布。

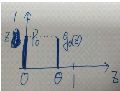
        简单明了的例子：

                已知，，

                且

                那么图像可以表示成

                                               

                求得的各距离值度量如下：

                

                当时，只有在EM距离下序列收敛到。

        定理1：已知是空间上的固定分布，是空间上的随机变量，是一个由和确定的函数，代表其分布，那么

            1.如果在上连续，也连续

            2.如果满足条件1，且是利普西兹函数，那么处处连续且可微。

            3. 和不满足以上性质。

第二部分：WassersteinGAN

  公式的下确界不好计算，改用来计算，其中为函数，也可以将用代替，那求的就是，因此等同于求解。

        定理3即是这样，并且可以得到              

                

                 问题就变成了找到一个满足利普西兹函数条件的函数，使得达到最大值。可以用带参数的神经网络确定函数，为使函数满足利普西兹条件，可以简单地将其参数截断到一个范围（比较简单）。被称为critic，生成模型的梯度传播为。

        模型基本算法：

                

第四部分实验结果

        1.说明这是一个有效的损失度量，和生成模型的收敛以及样本质量有关。

        2.提高了优化过程的稳定性。

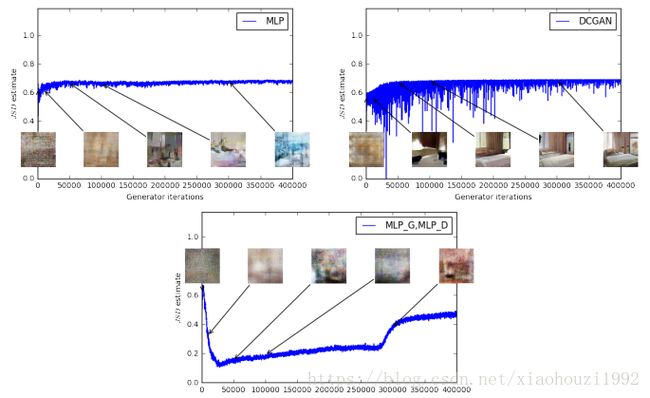
        1.有效的损失度量

            

            随着样本质量的增加，EM距离也在变小，最下面的这个是两个都是感知机，且有较大的学习率，所以样本质量没增加，W距离也没减小。

            

                随着样本质量增加，JS散度时上时下，和样本质量无关。

        2.提高稳定性

            GAN的判别模型和WGAN的critic固定为DCGAN的体系结构。

             

                                生成模型都是用DCGAN的生成器，左边为WGAN右边为GAN。

            

                生成模型都是用没有应用BN的DCGAN生成器，左边为WGAN右边为GAN。

            

                                         生成模型都为多层感知机，左边为WGAN右边为GAN。