你应该知道的建模的几种方法

携手ZRobot CEO乔杨为大家带来“企业级信用评分模型”系列课的第二课，本期课程乔杨老师主要介绍了建模的主要方法及在应用中需要注意的情况。以下是本次课程的部分干货。

建模方法主要分为非监督式学习、监督式学习、以及一些其它的组合性的学习方法。如下图所示：

下面我们对常用的建模方法做一下简单的分析：

一、主成分分析、因子分析、变量类聚分析

在实际建模过程中，主成分分析、因子分析、变量类聚分析。由于三种方法的理论基础和实际应用非常类似，都是用来减少变量数目的一种统计技术，因此我们将其放在一起介绍。

在模型开发过程中，数据集合中包含着几百上千个具备一定预测能力的变量，如果对这些变量一一进行分析，将耗费巨大的时间和精力，但取得的边际效益却非常小。因为诸多变量之间存在高度的相关性，反映潜在的共同信息维度。以统计学的术语来讲，这些潜在的共同信息维度在主成分分析中称为主成分，在因子分析中称作因子，在变量类聚分析汇总称为类聚。

以例子说明，近期拖欠历史是我们的一个潜在的信息维度，但是有很多变量都可以代表这一维度，比如在过去三个月中有一期以上拖欠次数，过去三个月中两期以上拖欠次数等。它们的信息是高度重叠的，所以可以用一个变量来代表该维度，不至于损失过多有用的信息。

那选择代表变量的标准是什么呢？

该变量与其所属的信息维度尽可能的高度相关，而与其他信息维度尽可能的低度相关。信息维度的多少可以由R统计程序根据一定统计指标自动决定，也可以由我们建模人员根据实际需求主观决定。

信息维度过多，则损失的信息量少，但保量的变量数目可能过多，从而不能充分达到减少变量、节约时间和精力的目的。反之，信息维度过少，则保留的变量数目也较少，有效地节约了时间和精力，但可能会损失过多的信息量。所以，它是一个需要平衡的过程。

优缺点如下：

二、类聚分析

类聚分析是一种对数据进行原始探索的统计方法，它是根据数据观察点之间的相似性把数据自然分组的一种结构，这种组就叫做类聚。打个比方，信用卡客户中循环信贷使用者可能倾向于分成同一个类聚，交易使用者可能划分成另外一个类聚。

类聚的划分结果取决于分析中所用的变量对相似性的界定，对类聚数目多少的要求。在实践中，最常用的列举方法有等级性类聚和非等级性类聚，等级性类聚一般呈现树形，通常有几个较低级别的类聚构成一个较高级别的类聚。等级性类聚可以通过一系列的合并或者分裂获得。

非等级性类聚通常是把所有的数据观察点分成K个不同类聚，目标是类聚内的数据观察点之间的总距离最小化。

通常我们用的k-means的方法就是这样一种类聚方法。一开始把所有的数据观察点分配到K个最初的类聚里，然后在每一次重新分组中计算每一个观察点和每一个类聚中心之间的距离，根据距离大小，观察点要么留在原先的类聚里面，要么被重新分配到距离最近的类聚里，类聚的中心也就是平均距离将被更新，这种重新分配的过程将持续到所有的观察点都离自己的类聚中心最近为止。

类聚分析常常被应用于市场营销之中，对消费者进行分类，可以发现消费者的一些行为特征和消费偏好，有针对性地制定一些营销策略，发布营销信息等。

优缺点如下：

三、回归分析

回归分析是一类确定变量与变量之间依赖关系的数据方法的总称。它分为线性回归、逻辑回归、多项式回归、非线性回归四类。

做回归分析的时候，有两个关键因素：函数形式、参数估计。在回归类模型中， 最常用的就是逻辑回归模型，也是目前在金融信贷领域应用最广泛的分析方法。

它跟线性回归模型的区别在于：

1. 逻辑回归模型的目标变量是二元性，而线性回归模型的目标变量是连续性的。

2. 逻辑回归模型预测的结果是介于零和一之间的概率，而线性回归模型预测结果可以是任何数值。

3. 逻辑回归模型预测结果与自变量之间是非线性关系，而线性回归模型预测结果和自变量之间是线性关系。

……

在选择预测变量进入逻辑回归模型的方法上，可以由建模人员根据统计指标和经验人为做选择，也可以由逻辑回归中的stepwise做自动选择。

Stepwise包含几种自动选择功能：前进型选择，模型开始不包括任何自变量，每一步加上对模型编辑贡献最大的自变量，直到模型达到最优；后退型删除，模型开始的时候是包含所有的候选自变量，然后每一步删除一个对模型编辑贡献最小的自变量值直到模型达到最优；复合型选择，同时包含前进型和后退型，每一步加入或删除一个自变量，直到模型达到最优。

Stepwise自动选择功能也具备一定的优缺点，优点可以说非常明显，它可以自动选择一组统计上合理的变量组成回归模型，可以对潜在的自变量进行试用，从中获得对自变量预测能力和相关性的洞察力。此外，还可以快速方便地对大量的候选自变量进行自动筛选。

缺点则在于，当自变量具备较高的相关性时，它会选择一些高相关性变量同时进入模型，一正一负地在一定程度上互相抵消影响，造成模型的不合理性。同时它对样本数据的敏感度高，存在一定的过度微调的可能，因此模型的稳定性和抗震荡性可能不够高，需要分析人员进行一些人工的调整。

逻辑回归模型的优缺点：

四、决策树模型

决策树模型是对总体进行连续地分割以预测一定目标变量结果的统计技术。一般包含若干层次的枝叶，同一枝叶内的个体非常相似，目标变量值接近；而不同枝叶之间的个体则存在较大的不相似性，也就是目标变量值相差较远。

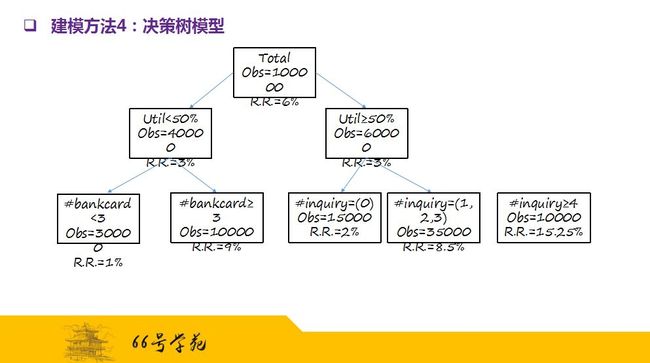
我们以市场反应为例，作为我们的目标变量的决策树模型例子，总体样本是10万个，市场总体反应率是6%。通过决策树算法，我们发现，第一个最佳的分割变量是信用额度的使用率，使用率小于50%的市场反应率是3%，而使用率大于等于50%的市场反应率是8%，可以看到两者的目标变量值有很大的差距。

对于使用率小于50%的样本组，下一个最佳分割变量是已有信用卡的张数，已有信用卡张数小于3的，反应率只有1%，显示这样的消费者对信用卡不感兴趣； 而已有信用卡大于等于3的，反应率为9%，显示消费者对信用卡有比较浓厚的兴趣。

而对使用率大于等于50%的样本组，下一个最佳分割变量是最近的信用卡申请查询次数。查询次数为0的反应率仅为2%，这是非常容易理解的，因为用户没有积极寻求新的信用；而查询次数大于等于4的，反应率高达15.25%，表示用户不仅大量信用且在迫切寻求新的信用，所以反应率极高。这样继续分割下去，直到达到停止分割的条件为止。

决策树模型可以对个体进行分割和预测，发现同质性的个体群从中得到洞察力，可以用来制定市场营销、风险管理等各方面的策略。

决策树模型的优缺点：

二分类模型的评估指标

考虑二分问题，可以将实例分成正类和负类两种。对于一个二分问题会出现四种情况，一是实例是正类，并且被预测成正类，即为真正类；如果实例是负类被预测成正类，称之为假正类。相应地，如果实例是负类被预测成负类，称之为真负类；正类被预测成负类则称为假负类。

我们对四类进行一个总结：

下面我们对这四类进行一个图表展示，并引入两个新名词。

二分类模型的输出其实是一个连续结果，反映的是与每个分类（通常是1）的相似程度或发生概率或排序能力。在实际运用中，需要确定一个阀值，比如说0.6，大于这个值的实例划归为“1”类，小于这个值则划到“0”类中。如果减小阀值，减到0.5，固然能识别出更多的正类，也就是提高了识别出的正例占所有正例的比例，即TPR,但同时也将更多的负实例当作了正实例，即提高了FPR。

为此，我们得出结论：对于同一个分类器，调整不同的阈值，只能同时提高TPR和FPR；为了对目标进行更好地区分需要改进分类器。