翻书问题或者走台阶问题。
问:共有n个台阶,每次只能上1个台阶或者2个台阶,共有多少种方法爬完台阶?共有n页书,每次只能翻1页或者2页书,共有多少种方法翻完全书?
ps:本质上是斐波那契数列问题。假设只有一个台阶,则只有一种跳法,f(1)=1;如果两个台阶,那么有两种跳法:1,一次跳一级,2,一次跳两级,f(2) = 2。如果大于2的n级台阶,那么一次跳一级台阶,剩下还有n-1级台阶,有f(n-1)种跳法。假如一次跳2级台阶,剩下n-2级台阶,有f(n-2)中跳法。这就表示f(n) = f(n-1)+f(n-2)。
function fibonacci(n) { if (n === 1 || n === 2) { return n; } else { return fibonacci(n-1) + fibonacci(n-2) } } // 一个记忆化的斐波那契数列 let tem = [0, 1] function fibonacci(n) { let result = tem[n] if(typeof result !== 'number') { result = fibonacci(n-1)+fibonacci(n-2) tem[n] = result // 将每次 fibonacci(n) 的值都缓存下来 } return result } // 动态规划:从底部开始解决问题, 将所有小问题解决掉, 然后合并成一个整体解决方案, 从而解决掉整个大问题 。 function fibonacci(n) { let last = 1; let nextLast = 1; let result = 1; for (let i = 2; i < n; ++i) { result = last + nextLast; nextLast = last; last = result; } return result; }
二分查找。
数组array包含了顺序的元素,[1,2,3,...,10],查找目标元素t是否在数组中。
我们已经提前知道数组是顺序排列的,比如递增顺序。
时间复杂度为O(logN)
递推公式:
f(N) = f(N/2) + O(1) = f(N/4) + 2 * O(1)
假设 N = 2 ^ M
最后可以推出
f(N) = O(logN)
let list = [1,2,3,4,5,6,7,8,9,10] function binarySearch(array, t) { let left = 0, right = array.length - 1; while(left <= right) { let mid = parseInt((right + left)/2) if(array[mid] < t) { left = mid + 1 } else if(array[mid] > t) { right = mid - 1 } else { return true } } return false } // 递归写法 function binarySearch2(array, t, left, right) { if(left > right) return -1 let mid = parseInt((right - left)/2) + left if(array[mid] === t) { return mid }else if(array[mid] < t){ return binarySearch2(array, t, mid + 1, right) }else if(array[mid] > t){ return binarySearch2(array, t, left, mid - 1) } } let test1 = binarySearch(list, 5) let test2 = binarySearch2(list, 5, 0, list.length-1) console.log(test1, test2)
贪心算法--最少硬币找零问题
所谓贪心,就是先选择当前阶段的最优解,不去考虑这次的选择会不会对未来造成影响,想要通过每个阶段的局部最优解,达到全局最优解。
假设你为一家自动售货机厂家编程序,自动售货机要每次找给顾客最少数量硬币,美国有以下面额的硬币:1美分、5美分、10美分、25美分。比如说要找36美分的零钱,我们可以用1个25美分、1个10美分和一个1美分。
(ps:找零问题,先找大额的硬币25分,依次递减)
function minCoinChange(amount, coins) { let minCoin = amount let count = 0 for(let i = 0, l = coins.length; i < l; i++) { if (coins[i] <= minCoin) { count += Math.floor(minCoin / coins[i]) console.log(coins[i] + '*' + Math.floor(minCoin / coins[i])) minCoin = minCoin % coins[i] } } return count } let counts = minCoinChange(61, [25, 10, 5, 1]) console.log(counts)
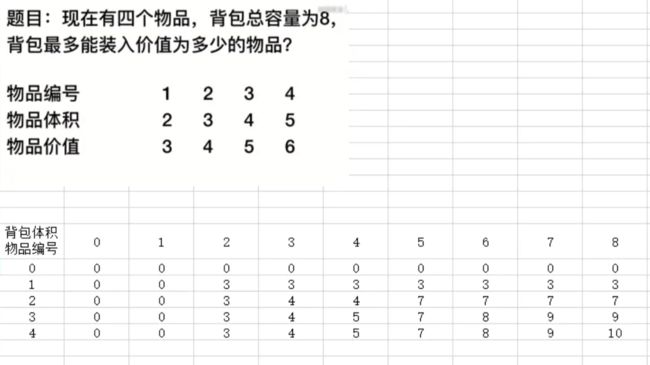
动态规划--01背包问题
function main(volume, value, c){ let tArray = [] let useGoodsNo = [] for(let i = 0, l = volume.length; i <= l; i++) { tArray[i] = [] useGoodsNo[i] = 0 for(let j = 0; j <= c; j++) { if(i == 0 || j == 0){ tArray[i][j] = 0 } } } volume.unshift(0) //让i = 1的时候对应的是1号物品 value.unshift(0) for(let i = 1, l = volume.length; i < l; i++) { // i从1开始 tArray[0][j]已经填满 for(let j = 1; j <= c; j++) { if(j < volume[i]){ tArray[i][j] = tArray[i-1][j] } else { //如果装了剩下的体积 let leftVolume = j - volume[i] // 当前物品的价值 let curValue = value[i] // 剩下的体积的价值是 (tArray[i - 1]因为0 1背包,不能重复放同个物品) let leftValue = tArray[i - 1][leftVolume] tArray[i][j] = Math.max(tArray[i-1][j], curValue+leftValue) } } } // 填满表格 console.table(tArray) // 逆向获取物品 let C = c for(let i = value.length-1; i > 0; i--){ if(tArray[i][C] > tArray[i-1][C]){ useGoodsNo[i] = 1 C = C - volume[i] } } console.table(useGoodsNo) // 所选的物品 console.log(tArray[value.length-1][c]) // 最大价值 } main([2,3,4,5], [3,4,5,6], 8)
展平数组
// 展平数组 [[1, 2], 3, [[[4], 5]]] => [1, 2, 3, 4, 5] function flatten(arr) { return [].concat( ...arr.map(x => Array.isArray(x) ? flatten(x) : x) ) }
随机打乱数组
function shuffle(arr) { for(let i = 0; i < arr.length-1; i++){ const j = i + Math.floor(Math.random() * (arr.length - i)) [arr[i], arr[j]] = [arr[j], arr[i]] } }
函数节流
// 函数节流 function throttle(func, delay = 60) { let lock = false return (...args) => { if(lock) return func(...args) lock = true setTimeout(()=> { lock = false }, delay) } }
柯里化
//对于curry(foo),g函数参数足够4个,就调用foo(a,b,c,d),如果小于4就返回一个可以继续积累参数的函数 const curry = func => { const g = (...allArgs) => allArgs.length >= func.length ? func(...allArgs) : (...args) => g(...allArgs, ...args) return g } const foo = curry((a, b, c, d) =>{ console.log(a, b, c, d) }) foo(1)(2)(3)(4) // 1 2 3 4 foo(1)(2)(3) // 不返回 const f = foo(1)(2)(3) f(4) // 1 2 3 4 5
Y组合子
const y = function(le) { return function (f) { return f(f) }(function (f) { return le( function(...x) { return (f(f))(...x) } ) }) } const curryY = func => y(g => { (...allArgs) => { allArgs.length >= func.length ? func(...allArgs) : (...args) =>g(...allArgs, ...args) } } ) const foo = curryY((a, b, c, d) => { console.log(a, b, c, d) }) foo(1)(2)(3)(4)
链表
链表中最简单的一种是单向链表,它包含两个域,一个信息域和一个指针域。这个链接指向列表中的下一个节点,而最后一个节点则指向一个空值。
function ListNode(val) { this.val = val this.next = null } let node1 = new ListNode(1) let node2 = new ListNode(2) let node3 = new ListNode(3) node1.next = node2 node2.next = node3 console.log(node1) function recursiveTraverse(head) { if(head != null) { console.log(head.val) recursiveTraverse(head.next) } } recursiveTraverse(node1) // 翻转一条单向链表 // 输入 1 -> 2 -> 3 -> null // 输出 3 -> 2 -> 1 -> null function reverseLinkedList(head){ let dummy = head let tem = dummy while(head != null && head.next != null){ dummy = head.next head.next = dummy.next dummy.next = tem tem = dummy } return dummy } let reverseLink = reverseLinkedList(node1) console.log(reverseLink)
二叉树
function TreeNode(val) { this.val = val this.left = null this.right = null } let root = new TreeNode(2) root.left = new TreeNode(1) root.right = new TreeNode(3) console.log(root) /* * 2 * / \ * 1 3 */ /* 中序遍历:( 定义: 1,中序遍历左子树 2,遍历根节点 3,中序遍历右子树 ) 前序遍历:( 定义: 1,遍历根节点 2,前序遍历左子树 3,前序遍历右子树 ) 后序遍历:( 定义: 1,后序遍历左子树 2,后序遍历右子树 3,遍历根节点 ) */ function inOrder(root) { if(root) { console.log('前',root.val) // 2 1 3 inOrder(root.left) console.log('中',root.val) // 1 2 3 inOrder(root.right) console.log('后',root.val) // 1 3 2 } } inOrder(root) /* 二叉查找树/二叉搜索树:( 定义: 左子树的所有节点的值小于根节点 右子树的所有节点的值大于根节点 左子树和右子树都是二叉查找树 ) 二叉搜索树的中序遍历就是排好序的元素。 */ function binarySearchTreeFind(root, target) { if(!root) return false if(root.val === target) { return true } else if(root.val < target){ return binarySearchTreeFind(root.right, target) } else if(root.val > target) { return binarySearchTreeFind(root.left, target) } } console.log(binarySearchTreeFind(root, 1))
栈
First In Last Out(FILO)
先进后出,后进先出
function Stack(){ this.stack = [] this.isEmpth = function(){ return this.size() === 0 } this.size = function() { return this.stack.length } // 出栈 this.pop = function(){ if(this.isEmpth()){ return null } else { return this.stack.pop() } } // 进栈 this.push = function (val){ return this.stack.push(val) } // 返回栈顶元素 this.peak= function(){ if(this.isEmpth()) { return null } else { return this.stack[this.stack.length - 1] } } } let test = new Stack() test.push(1) console.log(test.peak()) console.log(test.isEmpth()) test.pop() console.log(test.peak())
队列
First In First Out(FIFO)
先进先出
function Queue() { this.queue = [] this.size = function() { return this.queue.length } this.isEmpty = function(){ return this.size() === 0 } // 入队列 this.enqueue = function (val){ this.queue.unshift(val) } // 出队列 this.dequeue = function(){ if(this.isEmpty()){ return null } else { return this.queue.pop() } } } let test = new Queue() test.enqueue(1) test.enqueue(2) console.log(test.queue) test.dequeue() console.log(test.queue)