数据结构与算法--基础篇

目录

概念

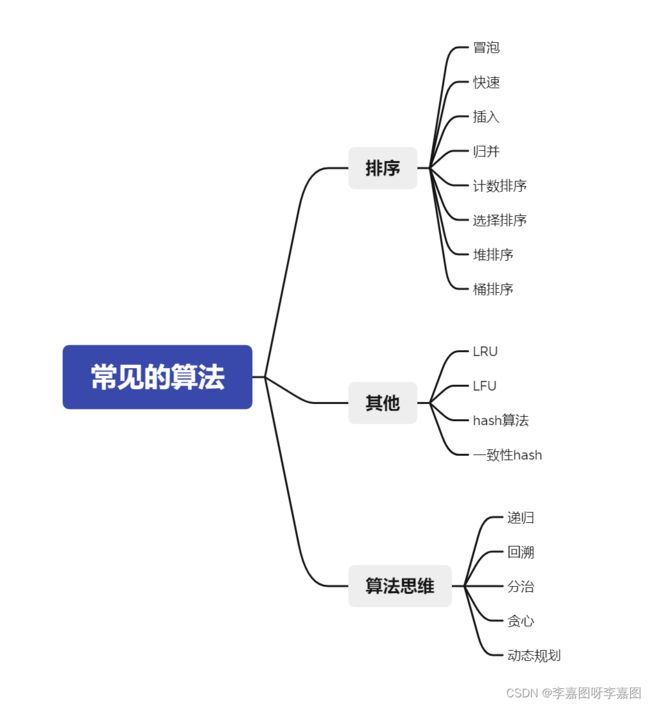
        常见的数据结构

        常见的算法

        算法复杂度

                空间复杂度

                时间复杂度

数据结构与算法基础

        线性表

                数组

                链表

                栈

                队列

        散列表

        递归

        二分查找

---

概念

        常见的数据结构

        常见的算法

        

        算法复杂度

                空间复杂度

        空间复杂度表示算法的存储空间与数据规模之间的增长关系，比如将一个数组拷贝到另一个数组中，就是相当于空间扩大了一倍:T(n)=O(2n)，忽略系数即为O(n)，由于现在硬件相对比较便宜，所以在开发中常会利用空间来换时间，比如 缓存技术 典型的数据结构中空间换时间是：Redis的跳跃表，实际开发中我们更关注代码的时间复杂度，而用于执行效率的提升。

                时间复杂度

        时间复杂度表示代码执行时间与数据规模间的增长关系，因此时间复杂度也称为渐进时间复杂度。

假设执行一行代码的时间为t，通过估算，代码的执行时间T(n)与执行次数成正比，记作：

        T(n)=O(f(n))

T(n) ： 代码执行时间

n ：      数据规模

f(n) ：  每行代码执行次数总和

O ：     代码的执行时间与 f(n) 表达式成正比

如  T(n)=O(2n+2) ，当n 无限大时，低阶、常量、系统都可以忽略，所以T(n)=O(n)

计算时间复杂度的技巧

1. 计算循环执行次数最多的代码
2. 总复杂度=量级最大的复杂度

        常见的时间复杂度

1. O(1)  常量级，代码执行时间不会随着数据规模增加而增加，实际应用中，通常使用冗余字段存储来将O(n)变成O(1),比如Redis中有很多这样的操作用来提升访问性能，比如:SDS、字典、跳跃表等。
2. O(logn)、O(nlogn)  快速排序、归并排序的时间复杂度都是O(nlogn)
3. O(n) 很多线性表都是O(n)， 比如数组的插入删除，链表的遍历 HashMap理论上是O(1)，但实际上是O(n)
4. O(n^2) 冒泡排序

数据结构与算法基础

        线性表

                数组

                  原理：在内存中开辟连续的内存空间存储相同类型的数据，物理上的连续的数据结构。

                  时间复杂度：读取和更新都是随机访问，复杂度 O(1)

                                        插入和删除涉及到数据移动，复杂度 O(n)

                  优缺点：随机访问效率高，但需要连续的空间，没有连续内存空间可能创建失败。

                  应用：数组是基础的数据结构，应用太广泛了，ArrayList、Redis、消息队列等等。
 

数组访问为何下标从0开始?  为何需要相同的类型？为何需要连续性分配？

假设首地址是：1000， int 是4字节（32位）

在进行随机元素寻址的时候： a[i]_address = a[0]_address + i * 4

因此相同的类型，连续性分配才能计算出位置，而从0开始相比与从1开始少了一步计算，效率更高。

                链表

                  原理：在物理上非连续、非顺序的数据结构，由若干节点（node）所组成，通过指针将各个节点关联起来，有效的利用零散的碎片空间。

                  时间复杂度：插入，更新，删除都是 O(1)，查找是 O(n)。

                  优缺点：省空间，插入效率高，但是查询效率低，不能随机访问。

                  应用：链表的应用也非常广泛，比如树、图、Redis的列表、LRU算法实现、消息队列等。

                栈

                  原理：栈属于线性结构的逻辑存储结构，栈中的元素只能先入后出，可以通过数组实现也可通过链表实现。

                  时间复杂度：入栈、出栈复杂度都是O(1)，扩容需要将元素拷贝到新的空间中，复杂度是 O(n)。

                  应用：函数调用记录，浏览器的前进后退功能。

                队列

                  原理：栈属于线性结构的逻辑存储结构，栈中的元素只能先进后出，可以通过数组实现也可通过链表实现。

                  时间复杂度：入队、出队复杂度都是O(1)。

                  应用：资源池、消息队列、命令队列等等。

        散列表

                 概念：散列表也叫哈希表（hash table），通过键（Key）和值（Value）的映射关系进行存储，根据Key，可以高效查找到它所匹配的Value，时间复杂度接近于O(1)。

                 存储原理：本质上也是一个数组，Key以字符串类型为主，通过hash函数将Key和数组下标进行转换，作用是将任意长度的输入通过散列算法转换成固定长度的的散列值。

//数组下标=取key的hashcode模数组的长度后的余数
index = HashCode (Key) % Array.length

插入数据时：                 

1.通过哈希函数，把Key转化成数组下标

2.如果数组下标对应的位置没有元素，就把这个Entry填充到数组下标的位置

3.插入的Entry越来越多时，不同的Key可能会禅师Hash冲突，冲突后可以通过 开放寻址法 或 链表法 解决冲突。

      开放寻址法：当一个Key通过哈希函数获得对应数组下标被占用时寻找下一个空档位置
      链表法：数组的每个元素不仅是个Entry对象，还是个链表的头节点。每个Entry对象通过next指针指向它的下个Entry节点。当新来的Entry映射到与之冲突的数组位置时，只需要插入到对应的链表中即可，默认next指向null

读取数据时：

1.通过哈希函数，把Key转化成数组下标

2.找到数组下标所对应的元素，如果key不正确则产生了hash冲突，顺着头节点遍历该单链表，再根据key即可取值

Hash扩容：

影响扩容的两个因素：

        Capacity：HashMap的当前长度
        LoadFactor：HashMap的负载因子（阈值），默认值为0.75f

当HashMap.Size >= Capacity×LoadFactor时，需要进行扩容

1. 创建一个新的Entry空数组，长度是原数组的2倍

2.重新Hash，遍历原Entry数组，把所有的Entry重新Hash到新数组中

JDK1.8前在HashMap扩容时，会反序单链表，这样在高并发时会有死循环的可能。

关于HashMap的实现，JDK 8和以前的版本有着很大不同。当多个Entry被Hash到同一个数组下标位置时，为了提升插入和查找的效率，HashMap会把Entry的链表转化为红黑树这种数据结构。

当链表长度为8，链表会转为红黑树；当链表长度为6，红黑树转换为链表；

红黑树的平均查找长度是log(n)，长度为8，查找长度为log(8)=3

链表的平均查找长度为n/2，当长度为8时，平均查找长度为8/2=4

链表长度如果是小于等于6，6/2=3，虽然速度也很快的，但是转化为树结构和生成树的时间并不会太短。

还有选择6和8的原因是：

中间差值7防止链表和树之间频繁的转换。假设一下，如果设计成链表个数超过8则链表转换成树结构，链表个数小于8则树结构转换成链表，如果一个HashMap不停的插入、删除元素，链表个数在8左右徘徊，就会频繁的发生树转链表、链表转树，效率会很低。

                 时间复杂度：

                写操作：O(1) + O(n) = O(n) n 为单链元素个数
                读操作：O(1) + O(n) n 为单链元素个数
                Hash冲突写单链表：O(n)
                Hash扩容：O(n) n是数组元素个数 rehash
                Hash冲突读单链表：O(n) n为单链元素个数        

                 优缺点：读写快，但是Hash表中元素没有被排序、Hash冲突、扩容需要重新计算hash

                 应用：HashMap，Redis字典，布隆过滤器，位图

        递归

                 概念：直接或者间接调用自身函数或者方法，本质上是一种循环

递归三要素：递归结束条件（有结束，无OOM）

                      递归函数功能（函数要做什么）

                      函数等价关系式（递归公式，一般是每次执行之间，或与个数之间逻辑关系）

例如：

//循环实现 
public static void print(String ss) { 
    for(int i=1;i<=5;i++){ 
        System.out.println(ss); 
    } 
}

//递归实现 
public static void print(String ss, int n) { 
    //递归条件 
    if(n>0){ 
        //函数的功能 
        System.out.println(ss);
        //函数的等价关系式 
        print(ss,n-1); 
    } 
}

public static void main(String[] args) { 
    //调用循环 
    print("Hello World"); 
    System.out.println("======================"); 
    
    //调用递归 
    print("Hello World", 5); 
}

递归要素：

        递归结束条件：n<=0

        函数的功能：System.out.println(ss);

        函数的等价关系式：fun(n)=fun(n-1)

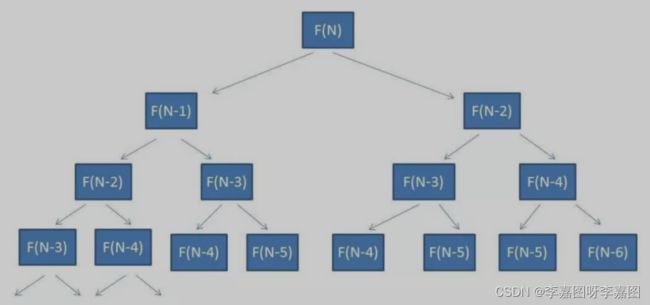
                 经典案例：斐波那契数列：0、1、1、2、3、5、8、13、21、34、55                  

                 规律：从第3个数开始，每个数等于前面两个数的和

                 递归分析：

                         函数的功能：返回n的前两个数的和

                         递归结束条件：从第三个数开始，n<=2

                         函数的等价关系式：fun(n)=fun(n-1)+fun(n-2)

                        

//递归实现 
public static int fun2(int n) { 
    if (n <= 1) 
        return n; 
    return fun2(n - 1) + fun2(n - 2); 
}

public static void main(String[] args) { 
    fun1(9); 
    System.out.println("=================================="); 
    System.out.println(fun2(9)); 
}

                 时间复杂度：斐波那契数列普通递归解法为O（2^n）

                 优缺点：代码简单，但是占用空间大，递归太深可能发生栈溢出，可能会有重复计算，可以通过备忘录或递归的方式去优化（动态规划）。

                 应用：递归作为基础算法，应用非常广泛，比如在二分查找、快速排序、归并排序、树的遍历上都有使用递归  回溯算法、分治算法、动态规划中也大量使用递归算法实现。

        二分查找

                 概念：二分查找（Binary Search）算法，也叫折半查找算法 。当数组是一个有序序列时使用二分查找效率很高，但是如果是无序的话，无法使用二分查找法

                 时间复杂度：O(logn)

                 优缺点：速度快，不占空间，不开辟新空间，但必须是有序的数组，数据量太小没有意义，但数据量也不能太大，因为数组要占用连续的空间

                 应用：有序的查找都可以使用二分法。