金融时间序列分析：3. First Demo By Python

0. 目录

金融时间序列分析：9. ARMA自回归移动平均模型
金融时间序列分析：8. MA模型实例（Python）
金融时间序列分析：7. MA滑动平均模型
金融时间序列分析：6. AR模型实例
金融时间序列分析：5. AR模型实例（Python）
金融时间序列分析：4. AR自回归模型
金融时间序列分析：3. First Demo By Python
金融时间序列分析：2. 数学分析模型
金融时间序列分析：1. 基础知识

---

1. 前言

金融时间序列分析：1. 基础知识
金融时间序列分析：2. 数学分析模型

前面2篇文章讲了金融时间序列分析的基础知识，本文简单介绍下怎么实战。
网上有很多用R语言进行金融时间序列分析的资料，但是用Python的不多，我在此介绍下怎么用Python操作，至于R语言怎么弄，读者随便在网上查查就好了。

PS: 在时间序列分析领域R比Python简单的多，如果单单是进行分析的话R就够了，但是要集成一个系统的话就得用Python。（个人之见）

---

2. 基础知识

2.1 基本步骤

1. 获取被观测系统时间序列数据；
2. 对数据绘图，观测是否为平稳时间序列；对于非平稳时间序列要先进行d阶差分运算，化为平稳时间序列；
3. 经过第二步处理，已经得到平稳时间序列。要对平稳时间序列分别求得其自相关系数ACF 和偏自相关系数PACF ，通过对自相关图和偏自相关图的分析，得到最佳的阶层 p 和阶数 q
4. 由以上得到的d、q、p ，选择合适的模型。然后开始对得到的模型进行模型检验。

本文只讨论前3步，至于后面的再提到具体的模型的时候回在补上。

2.2 Python时间序列分析

用Python进行时间序列分析需要用到下面一些库：
pandas,numpy,scipy,matplotlib,statsmodels

其中一些的基本使用参考下面的文章：
十分钟搞定pandas
Numpy Tutor
Python应用matplotlib绘图简介

---

3. 获取数据

有两种方式：
（1）从网络获取
这个参考以前的文章：
Python获取Yahoo股票数据

（2）从本地读取
在金融时间序列中CSV文件格式是一种非常简单的文件格式，最为常见的格式。

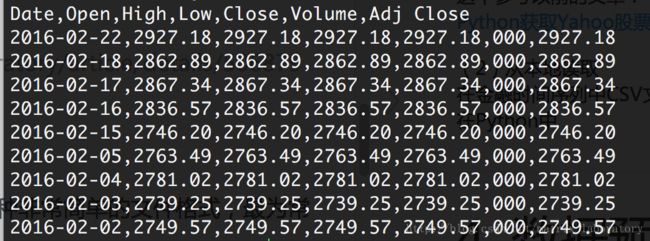
在Python中，Pandas中可以直接处理这种格式：

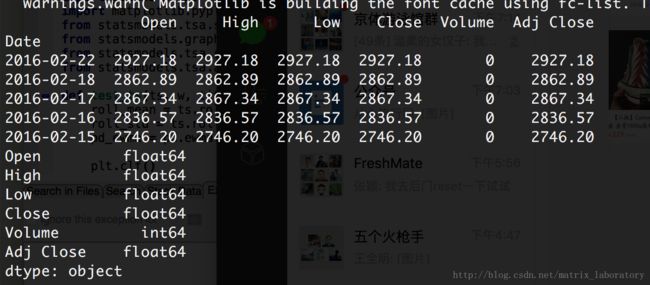
    data = pd.read_csv('./Yahoo/000001.SS.csv', index_col='Date')

    print data.head()
    print data.dtypes

此时Date的类型还不是时间，需要转化一下：

data.index = pd.to_datetime(data.index)

pandas数据索引：

    print "Select 2016:\n", data['2016']
    print 'Select 2016-02:\n', data['2016-02']
    print 'Select 2016-02-22:\n', data['2016-02-22']
    print 'Select 2016-02-22 : 2016-01-07:\n', data['2016-02-22':'2016-02-07']

---

4. 数据预处理

首先获取收盘数据，并将其翻转下顺序，因为前面的数据截图可以看到，数据是逆序的，所以需要处理下。

    ts = data['Close']
    ts = ts[::-1]

计算日收益率：

    ts_ret = np.diff(1)

对数收益率:

    ts_log = np.log(ts)
    ts_diff = ts_log.diff(1)
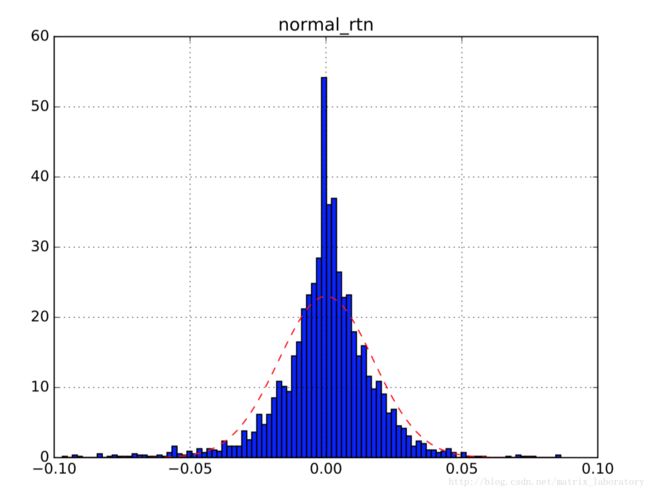
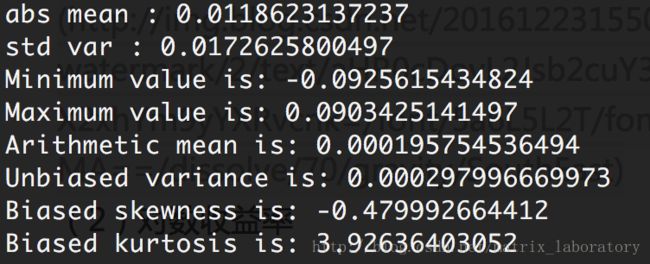
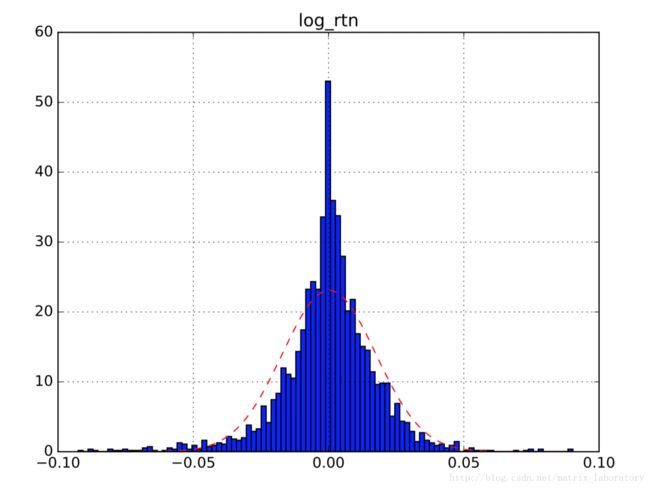
    ts_diff.dropna(inplace=True)

---

5. 数据展示

5.1 日线数据分析

def test_ts(ts, w, title='test_ts'):
    roll_mean = ts.rolling(window = w).mean()
    roll_std = ts.rolling(window = w).std()
    pd_ewma = pd.ewma(ts, span=w)

    plt.clf()
    plt.figure()
    plt.grid()
    plt.plot(ts, color='blue',label='Original')
    plt.plot(roll_mean, color='red', label='Rolling Mean')
    plt.plot(roll_std, color='black', label = 'Rolling Std')
    plt.plot(pd_ewma, color='yellow', label = 'EWMA')
    plt.legend(loc='best')
    plt.title('Rolling Mean & Standard Deviation')
    #plt.show()
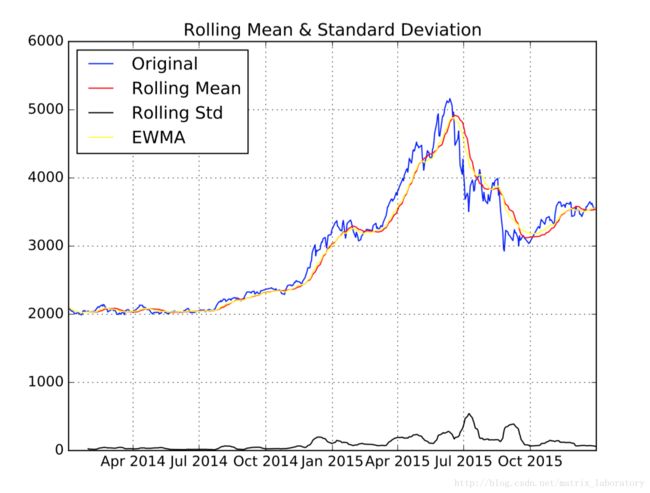
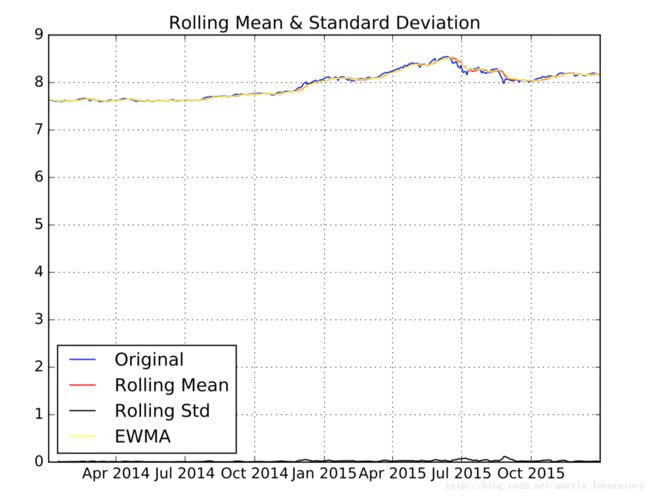
    plt.savefig('./PDF/'+title+'.pdf', format='pdf')

test_ts(ts['2014-01-01':'2015-12-31'], 20, title='test_org')

test_ts(ts_log['2014-01-01':'2015-12-31'], int(adf_res['Lags Used']), title='test_log')

5.2 收益率分析

（1）简单收益率


（2）对数收益率

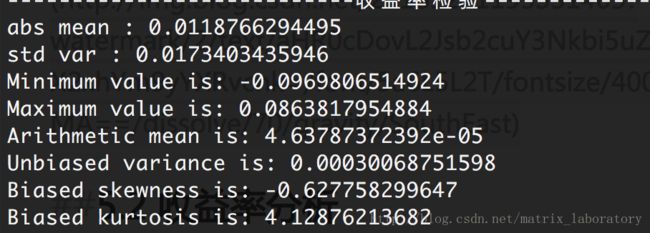
从上面显示图可以看出，无论简单收益率还是对数收益率都具有尖峰厚尾现象。

---

6. 平稳性检验

平稳性检验：观察法和单位根检验法

6.1 观察法：

最简单稳定性检验就是肉眼观察下，只要没有明显趋势，就好^_^!

观察法，通俗的说就是通过观察序列的趋势图与相关图是否随着时间的变化呈现出某种规律。所谓的规律就是时间序列经常提到的周期性因素，现实中遇到得比较多的是线性周期成分，这类周期成分可以采用差分或者移动平均来解决，而对于非线性周期成分的处理相对比较复杂，需要采用某些分解的方法。下图为航空数据的线性图，可以明显的看出它具有年周期成分和长期趋势成分。

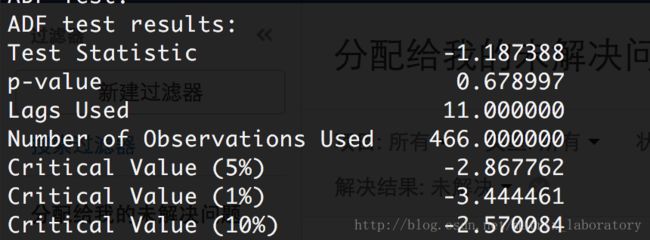
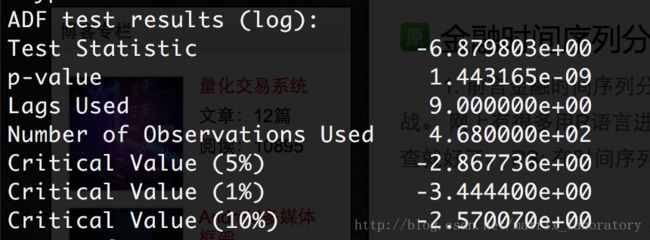
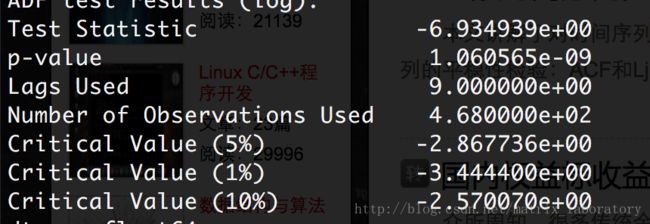
6.2 单位根检验 ADF

下面谈谈单位根检验。。。
在时间序列分析中，通常采用ADF进行稳定性检验。

下面的代码是如何用python进行ADF检验：

def adf_test(ts):
    adftest = adfuller(ts)
    adf_res = pd.Series(adftest[0:4], index=['Test Statistic','p-value','Lags Used','Number of Observations Used'])

    for key, value in adftest[4].items():
        adf_res['Critical Value (%s)' % key] = value
    return adf_res

日收盘数据
检验结果分析：

p值为：0.67不能拒绝原假设

简单收益率

p值接近于0，拒绝原假设

对数收益率

p值接近于0，拒绝原假设

---

7. 定阶

本来不打算在这篇文章中解释这快内容，只有讲了分析模型后才会这块有大致的概念。
所以本文在此不会细谈，之后有机会慢慢谈。

7.1 什么是定阶？

简单的理解就是找到时间序列的周期，比如说气温这一项，就有明显的年度周期性，前几年的同期数据对预测当年的气温有极大的参考意义。
从统计学上讲就是寻找是得ACF（样本自相关系数）最大的时间间隔。

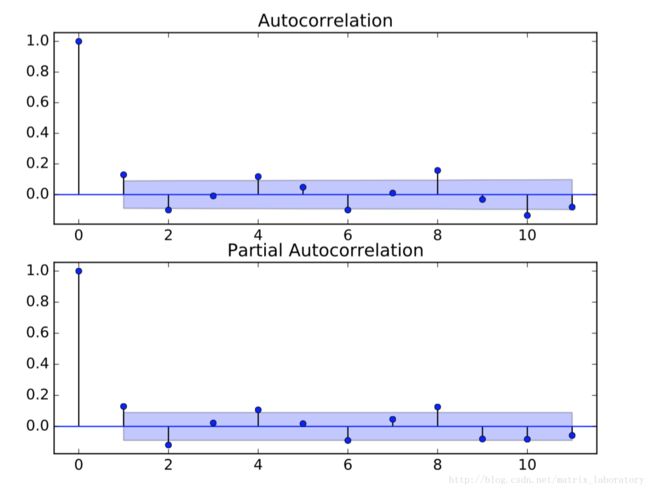
7.2 Python如何定阶

常用定阶方法是ACF和PACF。

def draw_acf_pacf(ts, w):
    plt.clf()
    fig = plt.figure()
    ax1 = fig.add_subplot(211)
    plot_acf(ts, ax = ax1, lags=w)
    ax2 = fig.add_subplot(212)
    plot_pacf(ts, ax=ax2, lags=w)

    #plt.show()
    plt.savefig('./PDF/test_acf_pacf.pdf', format='pdf')

对数收益率ACF分析：