遗传算法求函数极值(含MATLAB代码实现)
介绍转载自https://blog.csdn.net/xujinpeng99/article/details/6211597,后面用自己设置的函数进行实验。
引言:遗传算法求函数极值算是遗传算法的一种最简单的应用,这里就介绍一种简单的,全文基本翻译自codeproject的一篇文章,作者为Luay Al-wesi,软件工程师。例子中的函数为y = -x2+ 5 ,大家可以将其改为其他复杂一些的函数,比如说f=x+10sin(5x)+7cos(4x)等。
一、编码以及初始种群的产生
编码采用二进制编码,初始种群采用矩阵的形式,每一行表示一个染色体,每一个染色体由若干个基因位组成。关于染色体的长度(即基因位的个数)可根据具体情况而定。比如说根据要求极值的函数的情况,本文的染色体长度为6,前5个二进制构成该染色体的值(十进制),第6个表示该染色体的适应度值。长度越长,表示解空间搜索范围越大。关于如何将二进制转换为十进制,这个应该很简单,文后的C代码中函数x即为转换函数。
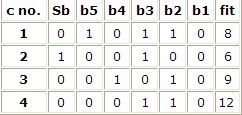
初始种群结构如下图所示:
图1
该初始种群共有4个染色体,第一列表示各个染色体的编号,第2列表示该染色体值的正负号,0表示正,1表示负。第3列到第7列为二进制编码,第8列表示各个染色体的适应度值。第2列到第7列的0-1值都是随机产生的。
二、适应度函数
一般情况下,染色体(也叫个体,或一个解)的适应度函数为目标函数的线性组合。本文直接以目标函数作为适应度函数。即每个染色体的适应度值就是它的目标函数值,f(x)=-x2+ 5。
三、选择算子
初始种群产生后,要从种群中选出若干个体进行交叉、变异,那么如何选择这些个体呢?选择方法就叫做选择算子。一般有轮盘赌选择法、锦标赛选择法、排序法等。本文采用排序法来选择,即每次选择都选出适应度最高的两个个体。那么执行一次选择操作后,得到的新种群的一部分为下图所示:
图2
四、交叉算子
那么接下来就要对新种群中选出的两个个体进行交叉操作,一般的交叉方法有单点交叉、两点交叉、多点交叉、均匀交叉、融合交叉。方法不同,效果不同。本文采用最简单的单点交叉。交叉点随机产生。但是交叉操作要在一定的概率下进行,这个概率称为交叉率,一般设置为0.5到0.95之间。交叉后产生的新个体组成的新种群如下:
图3
黑体字表示子代染色体继承母代个体的基因情况。
五、变异
变异就是对染色体的结构进行变异,使其改变原来的结构(值也就改变),达到突变进化的目的。变异操作也要遵从一定的概率来进行,一般设置为0到0.5之间。本文的变异方法直接采取基因位反转变异法,即0变为1,1变为0。要进行变异的基因位的选取也是随机的。
六、终止规则
遗传算法是要一代一代更替的,那么什么时候停止迭代呢?这个规则就叫终止规则。一般常用的终止规则有:若干代后终止,得到的解达到一定目标后终止,计算时间达到一定限度后终止等方法。本文采用迭代数来限制。
%VELASCO, Gimel David F.
%2012-58922
%Cmsc 191
%Genetic Algorithm
%Final Exam
%for runs=1:3
clear;
tic;
%%%%%%%%%%%%%%%%%%%%%%%%%%%INPUT ARGUMENTS%%%%%%%Sir Joel, dito po%%%%%%%%%
CostF =2; % | 1 - DE JONGS | 2 - AXIS PARALLEL HYPER-ELLIPSOID | 3 - ROTATED HYPER-ELLIPSOID | 4 - RASTRIGINS | ow - ACKLEYS |
nVar = 3; %number of dimensions
VarSize = zeros(nVar); %stores the fittest chromosome per iteration
VarMin = -5.12; %upper bound of variable value
VarMax = 5.12; %lower bound of variable value
MaxGen = 100000; %maximum number of generations
nPop = 5000; %chromosome population
nSel = 1; % | 1 - Tournament Selection | ow - Roulette Wheel Selection |
mu = 0.1; %mutation rate
sigma = 0.25; %crossover rate
cxver= 2; % | 1 - Single point Crossover | ow - Three point Crossover |
tol = 0.0000025; %fitness tolerance (minimization problem)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%STEP 1: Initialization
test_func = CostF;
ub = VarMax;
lb = VarMin;
ulb = ub; %temporary bengat
tpl = nVar;
popsize = nPop; %Population Size
maxgens = MaxGen; %Maximum Generations
pc = sigma; %crossover rate
pm = mu; %mutation rate
%tol = tol; %tolerance
iteration_array = zeros(1);
fittest_array = zeros(1);
solution_array = VarSize;
Chromosome = zeros(popsize,tpl);
for i=1:popsize
Chromosome(i,:) = 2*ulb*(rand(1,tpl)-0.5); %initializing first generation
end
%%%%%%%%%%%%%%%%%%%%%%%%%GENETIC ALGORITHM%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%
for generation=1:maxgens %LOOPS STEPS 2 to 5(最大的迭代次数)
%STEP 2: Selection
if nSel == 1
%(锦标赛选择法)
for i=1:popsize/4 %Tournament process
red = abs(floor(popsize*rand(1))) + 1; %两个随机染色体
blu = abs(floor(popsize*rand(1))) + 1;
if OBJFUNC(Chromosome(red,:),tpl,test_func) > OBJFUNC(Chromosome(blu,:),tpl,test_func) %competition
Chromosome(red,:) = Chromosome(blu,:); %Blue Wins the tournament and overwrites Red
else
Chromosome(blu,:) = Chromosome(red,:); %Red Wins the tournament and overwrites Blue
end
end
else
%轮盘赌选择法
F_obj = zeros(1);
for i=1:popsize
F_obj(i) = OBJFUNC(Chromosome(i,:),tpl,test_func);
end
Total = 0;
Fitness = zeros(1);
P = zeros(1);
C = zeros(1);
R = zeros(1);
NewChromosome = zeros(tpl);
for i=1:popsize
Fitness(i) = 1/(1+F_obj(i));
Total = Total + Fitness(i);
end
for i=1:popsize
P(i) = Fitness(i)/Total;
end
ctr = 0;
for i=1:popsize
ctr = ctr + P(i);
C(i) = ctr;
end
for i=1:popsize
R(i) = rand(1);
end
for i=1:popsize
NewChromosome(i,:) = zeros(1,tpl);
for j=1:popsize-1
if R(i) > C(j) && R(i) <= C(j+1)
NewChromosome(i,:) = Chromosome(j,:);
end
end
if NewChromosome(i,:) == zeros(1,tpl)
NewChromosome(i,:) = Chromosome(1,:);
end
end
for i=1:popsize
Chromosome(i,:) = NewChromosome(i,:);
end
end
%%
R = rand(1,popsize);
k = zeros(1);
PChromosome = zeros(tpl);
cp = zeros(1);
cp3 = zeros(3);
ctr = 0; %holds number of parents
for i=1:popsize
if R(i) < pc
%选择父代
ctr = ctr + 1;
k(ctr) = i; %will save the positions of the parent chromosomes
PChromosome(ctr,:) = Chromosome(i,:);
end
end
if ctr == 0 %if no parents were selected for the next generation
continue;
end
%%
%STEP 3: 交叉
if cxver == 1 %单点交叉
for i=1:ctr
cp(i) = floor(abs((tpl-1)*rand(1)))+1; %crossover points
end
for i=1:ctr-1
Chromosome(k(i),:) = CROSSOVER(PChromosome(i,:),PChromosome(i+1,:),cp(i),tpl); %crossover ci and ci+1
end
Chromosome(k(ctr),:) = CROSSOVER(PChromosome(ctr,:),PChromosome(1,:),cp(ctr),tpl); %crossover ck and c1
else %三点交叉
for i=1:ctr
cp3(i,:) = floor(abs((tpl-1)*rand(1,3)))+1; %crossover points
end
for i=1:ctr-1
Chromosome(k(i),:) = CROSSOVER3(PChromosome(i,:),PChromosome(i+1,:),cp3(i,:),tpl); %crossover ci and ci+1
end
Chromosome(k(ctr),:) = CROSSOVER3(PChromosome(ctr,:),PChromosome(1,:),cp3(ctr,:),tpl); %crossover ck and c1
end
%%
%STEP 4: 变异
%Per Chromosome mutation
mu = round(pm*popsize); %#ofchromosomestomutate = mutationrate*populationsize
for i=1:mu
cngn = abs(floor(popsize*rand(1))) + 1; %random popsize number
q = OBJFUNC(Chromosome(cngn,:),tpl,test_func);
if q < 1
Chromosome(cngn,:) = 2*ulb*q*(rand(1,tpl)-0.5); %mutation
else
Chromosome(cngn,:) = 2*ulb*(rand(1,tpl)-0.5);
end
end
%%
%STEP 5: 终止评价
F_obj = zeros(1);
for i=1:popsize
F_obj(i) = OBJFUNC(Chromosome(i,:),tpl,test_func);
end
%%
fittest = F_obj(1);
for i=1:popsize
fi = 1;
if fittest > F_obj(i)
fittest = F_obj(i);
fi = i;
end
end
%fprintf('Fittest: %.16f\t\tRuntime: %.2f seconds\n',fittest,toc);
%disp(Chromosome(fi,:))
fittest_array(generation) = fittest;
iteration_array(generation) = generation;
solution_array(generation,:) = Chromosome(fi,:);
if fittest < tol %&& abs(DECODE(Chromosome(fi,:),tpl) - round(DECODE(Chromosome(fi,:),tpl))) < 0.00005
break;
end
%Step 6: 重复进行代数迭代
end
%%
%STEP 7: 得出最优染色体
if test_func == 1
fprintf('====================DE JONGS FUNCTION=============================\n');
elseif test_func == 2
fprintf('==============AXIS PARALLEL HYPER-ELLIPSOID FUNCTION==============\n');
elseif test_func == 3
fprintf('===============ROTATED HYPER-ELLIPSOID FUNCTION====================\n');
elseif test_func == 4
fprintf('====================RASTRIGINS FUNCTION===========================\n');
else
fprintf('=====================ACKLEYS FUNCTION=============================\n');
end
fprintf('====================GENETIC ALGORITHM=============================\n');
if nSel == 1
fprintf('Tournament Selection. ');
else
fprintf('Roulette-Wheel Selection. ');
end
if cxver == 1
fprintf('Single Point Crossover.\n');
else
fprintf('Triple Point Crossover.\n');
end
fprintf('===================Generations: %d\tPopulation: %d===========\n',maxgens,popsize);
%fprintf('Final Generation\n');
%Chromosome = SORT(Chromosome,popsize,tpl,test_func);
%disp(Chromosome)
fprintf('Generation Number: %d\nPopulation Size: %d\nCrossover Rate: %.2f\nMutation Rate: %.2f\nDimensions: %d\n',maxgens,popsize,pc,pm,tpl);
%fprintf('\nThe Fittest Chromosome is\n');
%disp(Chromosome(fi,:)')
%fprintf('Using Tournament Selection\n');
fprintf('Fitness Function Value of %.16f\nTotal Runtime of %f seconds\n',fittest,toc);
fprintf('The Root for Test Function %d is:\n',test_func);
disp(Chromosome(fi,:))
fprintf('==================================================================\n');
%%
figure
subplot(2,1,1);
plot(iteration_array,fittest_array);
legend('Cost Function Value');
xlabel('Generation');
ylabel('Fitness of fittest Chromosome');
solution_array = transpose(solution_array);
subplot(2,1,2);
plot(iteration_array,solution_array);
xlabel('Generation');
ylabel('Solution of fittest Chromosome');
%%
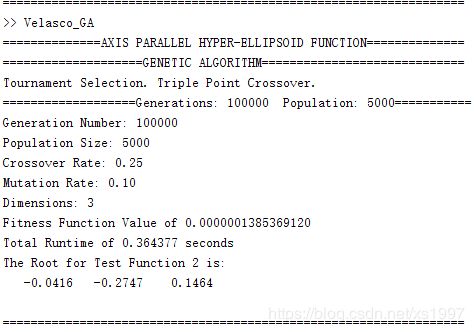
%end结果: