基于遗传算法和模拟退火算法改进的混合模拟退火算法(解决求函数极值问题,MATLAB代码已实现)
基本思想:
混合模拟退火算法时遗传算法和模拟退火算法的结合,在混合模拟退火算法中使用了大量的样本作为问题的可能解决方案而不是将单个样本作为一个问题的可能解决方案。对遗传算法中适应的概念进行相应改进。
混合模拟退火的算法步骤如下:
(1)将系统温度T设置为足够高的值。
(2)随机的初始化人口。
(3)人口随机初始化从现有种群中重复生成每个新种群,直到系统温度T达到一个令人满意的最小值。
1)执行N/2次;
2)从N个人口中随机选择两个父母;
3)执行交叉操作产生两个后代,然后进行变异操作;
4)在子女和父母之间进行玻尔兹曼试验;
5)用玻尔兹曼实验获胜者复写父母代染色体;
6)周期性地降低系统温度T。
(4)得出最优解
其中涉及到的相关改进操作如下:
交叉:
1.如果选择的父母要进行交叉,在他们的染色体上的一个随机点进行单点交叉产生两个孩子,然后转到变异操作。
2.如果父母不在交叉概率范围内,父母将进行比较。更好的父进程会覆盖另一个父进程。不进行变异操作。
变异:
1.生成的每个子节点将执行步骤2到4。
2.随机选择邻居作比较,一个后代的n个邻居的扰动为N*Pn。
3.比较扰动状态下的解,如果邻居比孩子好,就把孩子换掉。
4.基于变异操作重新复写子代染色体
玻尔兹曼试验:
1.用抛硬币的方式选择一个或两个接受/拒绝。
2.如果选择双重接受/拒绝,则取Ei = Eparent1 + Eparent2;Ej = Echild1 + Echild2
3.如果选择单一的接受/拒绝,取Ei = Eparent;Ej = Echild。这样做是为了测试每个孩子的父母。
4.最后用实验的获胜的来复写父代染色体
clear;
tic;
%%%%%%%%%%%%%%%%%%%%%%%%%%%INPUT ARGUMENTS%%%%%%%Sir Joel, dito po%%%%%%%%%
CostF = 2; % | 1 - DE JONGS | 2 - AXIS PARALLEL HYPER-ELLIPSOID | 3 - ROTATED HYPER-ELLIPSOID | 4 - RASTRIGINS | ow - ACKLEYS |
nVar = 3;
VarSize = zeros(nVar);
VarMin = -5.12; %upper bound of variable value
VarMax = 5.12; %lower bound of variable value
MaxIt = 100000;
T0 = 100000;
Tf = 0.0000000000000001;
alpha = 0.7;
nPop = 1000;
nMove = 50;
mu = 0.05;
sigma = 0.9;
%%
%%%%%%%%%%%%%%%%%%%%%%%%%%Initialization Section%%%%%%%%%%%%%%%%%%%%%%%%%%%
initial_T = T0; %initial temperature of the system
cooling_stop = Tf; %cooling stops when it reaches this temperature
test_func = CostF; %sets the number of w/c test function to be solved
popsize = nPop; %Population Size
pc = sigma; %crossover rate
pm = mu; %mutation rate
cooling_ratio = alpha; %sets the cooling ratio to 0.8 i.e. 0.7 < 0.8 < 0.9
ub = VarMax;
lb = VarMin;
ulb = ub; %upper and lower bound
tpl = nVar; %dimensions
num_neigh = nMove; %number of neighbors to consider
iteration_array = zeros(1);
fittest_array = zeros(1);
solution_array = VarSize;
%%
%%%%%%%%%%%%%%%%%%%%%%%%%HYBRID SIMULATED ANNEALING%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%I
cooling_sched = zeros(1); %pre-allocation for speed
cooling_sched(1) = initial_T; %initializes the cooling schedule T0
%II
Chromosome = zeros(popsize,tpl);
for i=1:popsize
Chromosome(i,:) = 2*ulb*(rand(1,tpl)-0.5); %initializing first generation
end
%%
sched = 1; %index / iteration
while cooling_sched(sched) > cooling_stop %iteration will stop if the cooling temperature reached less than 0.00000001 迭代终止条件
T = cooling_sched(sched); %设置温度T的值
%执行N/2次
for j=1:popsize/2
%III.a.i. Select two parents at random随机选择两个父母
red = abs(floor(popsize*rand(1))) + 1; %two random chromosomes to compete
blu = abs(floor(popsize*rand(1))) + 1; %red and blu hold the index of the parents
%III.a.ii. Generate two offsprings产生两个后代
%%Recombination Operator (CROSSOVER)重新结合,交叉
pc_trial = rand(1);
if pc_trial < pc %if trial made it in the crossover rate是否实验在交叉率下进行
cp = floor(abs((tpl-1)*rand(1)))+1; %random crossover point随机交叉点
Child_Chromosome(1,:) = CROSSOVER(Chromosome(red,:),Chromosome(blu,:),cp,tpl); %crossover red and blu两个父母进行交叉
Child_Chromosome(2,:) = CROSSOVER(Chromosome(blu,:),Chromosome(red,:),cp,tpl); %they will have two children产生两个孩子
%%Neighborhood Operator (MUTATION)变异操作
for k=1:2
x_sol = Child_Chromosome(k,:);
for i=1:num_neigh
adrs = abs(floor(popsize*rand(1))) + 1; %获取人口中某个邻居的随机地址
x_tmp = Chromosome(adrs,:); %随机选择额一个邻居做比较. with a decreasing amount of randomness
if OBJFUNC(x_tmp,tpl,test_func) < OBJFUNC(x_sol,tpl,test_func) %比较之后选择好的
x_sol = x_tmp;
elseif OBJFUNC(x_tmp,tpl,test_func) > OBJFUNC(x_sol,tpl,test_func) %if not, change the solution if it is lucky
delta = OBJFUNC(x_tmp,tpl,test_func) - OBJFUNC(x_sol,tpl,test_func);
p = P(delta,T);
q = rand(1);
if q <= p
x_sol = x_tmp;
end
end
end
Child_Chromosome(k,:) = x_sol; %基于变异操作重新复写子代染色体
end
%%III.a.iii. Boltzman Trials进行玻尔兹曼实验
ARpossibility = rand(1); % <0.5 - Single Acceptance/Rejection | >=0.5 - Double Acceptance/Rejection
if ARpossibility < 0.5 %%Case 1: Double Acceptance/Rejection
E1 = OBJFUNC(Chromosome(red,:),tpl,test_func) + OBJFUNC(Chromosome(blu,:),tpl,test_func);
E2 = OBJFUNC(Child_Chromosome(1,:),tpl,test_func) + OBJFUNC(Child_Chromosome(2,:),tpl,test_func);
bp = BOLTZMAN(E1,E2,T);
bp_trial = rand(1);
if bp_trial >= bp
%%III.a.iv. Overwrite Parents with the Trial Winner
Chromosome(red,:) = Child_Chromosome(1,:);
Chromosome(blu,:) = Child_Chromosome(2,:);
end
else %%Case 2: Single Acceptance/Rejection
E1 = OBJFUNC(Chromosome(red,:),tpl,test_func);
E2 = OBJFUNC(Child_Chromosome(1,:),tpl,test_func);
bp = BOLTZMAN(E1,E2,T);
bp_trial = rand(1);
if bp_trial >= bp
%%III.a.iv. Overwrite Parents with the Trial Winner
Chromosome(red,:) = Child_Chromosome(1,:); %offsprings wins the trial
end
E1 = OBJFUNC(Chromosome(red,:),tpl,test_func);
E2 = OBJFUNC(Child_Chromosome(2,:),tpl,test_func);
bp = BOLTZMAN(E1,E2,T);
bp_trial = rand(1);
if bp_trial >= bp
%%III.a.iv. Overwrite Parents with the Trial Winner
Chromosome(red,:) = Child_Chromosome(2,:); %offsprings wins the trial
end
E1 = OBJFUNC(Chromosome(blu,:),tpl,test_func);
E2 = OBJFUNC(Child_Chromosome(1,:),tpl,test_func);
bp = BOLTZMAN(E1,E2,T);
bp_trial = rand(1);
if bp_trial >= bp
%%III.a.iv. Overwrite Parents with the Trial Winner
Chromosome(blu,:) = Child_Chromosome(1,:); %offsprings wins the trial
end
E1 = OBJFUNC(Chromosome(blu,:),tpl,test_func);
E2 = OBJFUNC(Child_Chromosome(2,:),tpl,test_func);
bp = BOLTZMAN(E1,E2,T);
bp_trial = rand(1);
if bp_trial >= bp
%%III.a.iv. Overwrite Parents with the Trial Winner
Chromosome(blu,:) = Child_Chromosome(2,:); %offsprings wins the trial
end
end
%%
else %if the whole trial did not make it inside the crossover rate, it will have a tournament
if OBJFUNC(Chromosome(red,:),tpl,test_func) > OBJFUNC(Chromosome(blu,:),tpl,test_func) %competition
Chromosome(red,:) = Chromosome(blu,:); %Blue Wins the tournament and overwrites Red
else
Chromosome(blu,:) = Chromosome(red,:); %Red Wins the tournament and overwrites Blue
end
end
end
%III.b. Periodically Lower T周期性的降低温度T
%%
%Post-Iteration-Evaluation
F_obj = zeros(1);
for i=1:popsize
F_obj(i) = OBJFUNC(Chromosome(i,:),tpl,test_func);
end
%%
fittest = F_obj(1);
for i=1:popsize
fi = 1;
if fittest > F_obj(i)
fittest = F_obj(i);
fi = i;
end
end
%%
fittest_array(sched) = fittest;
iteration_array(sched) = sched;
solution_array(sched,:) = Chromosome(fi,:);
cooling_sched(sched+1) = T*(cooling_ratio)^sched;
sched = sched+1;
if sched > MaxIt
break;
end
end
%%
%SOLUTION
if test_func == 1
fprintf('====================DE JONGS FUNCTION=============================\n');
elseif test_func == 2
fprintf('==============AXIS PARALLEL HYPER-ELLIPSOID FUNCTION==============\n');
elseif test_func == 3
fprintf('===============ROTATED HYPER-ELLIPSOID FUNCTION====================\n');
elseif test_func == 4
fprintf('====================RASTRIGINS FUNCTION===========================\n');
else
fprintf('=====================ACKLEYS FUNCTION=============================\n');
end
fprintf('==================HYBRID SIMULATED ANNEALING=======================\n');
fprintf('Population Size: %d\tCrossover Rate: %.2f\tMutation Rate: %.2f\tCooling Ratio: %.1f\n',popsize,pc,pm,cooling_ratio);
fprintf('Minimum Energy:\t\t\t\t\t\t\t\t\t%.16f\nTotal Runtime:\t\t\t\t\t\t\t\t\t%f seconds\nFinal Temperature:\t\t\t\t\t\t\t\t%.16f\n',fittest,toc,cooling_sched(sched));
fprintf('Global Minimum is at:\t\t\t\t\t\t');
disp(Chromosome(fi,:))
fprintf('===================================================================\n');
%%
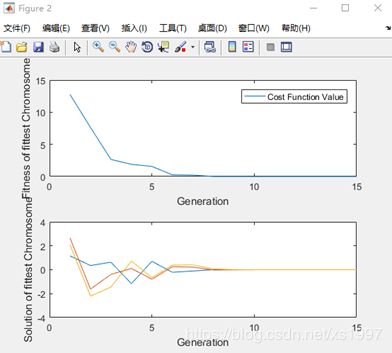
figure
subplot(2,1,1);
plot(iteration_array,fittest_array);
legend('Cost Function Value');
xlabel('Generation');
ylabel('Fitness of fittest Chromosome');
solution_array = transpose(solution_array);
subplot(2,1,2);
plot(iteration_array,solution_array);
xlabel('Generation');
ylabel('Solution of fittest Chromosome');
%%对于一个基准测试函数所做实验结果如下:
参数设置:
人口数:1000 交叉率:0.9 变异率:0.05 冷却比率:0.7
最小能量值:0.0149937292529736
邻居数:50
最大迭代次数:100000
初试温度:T0 = 100000
最终温度:Tf = 0.000000000000001;
温度下降率:alpha = 0.7;
目标函数值:0.0000005086849880
运行时间:1.743826 s
最终冷却温度:0.0000000000000000
全局最小值(-0.0444 -0.1056 0.0432)
鉴于很多同学问相关完整的代码实现,我把完整的代码和大家分享,希望能给大家帮助啦~
项目完整代码