机器学习模型评估指标

原文章地址：http://blog.csdn.net/heyongluoyao8/article/details/49408319#

机器学习模型评价(Evaluating Machine Learning Models)-主要概念与陷阱

前言

  本文主要解释一些关于机器学习模型评价的主要概念，与评价中可能会遇到的一些陷阱。如训练集-验证集二划分校验（Hold-out validation）、交叉校验（Cross-validation）、超参数调优(hyperparameter tuning)等。这三个术语都是从不同的层次对机器学习模型进行校验。Hold-out validation与Cross-validation是将模型能够更好得对将来的数据（unseen data）进行拟合而采用的方法。Hyperparameter tuning是一种模型选择方法。
  机器学习是一门跨学科领域，涉及到统计学、计算机科学、最优化理论、信息理论、神经科学、理论物理以及其他领域。同时，机器学习也是一门非常年轻的学科。机器学习的大规模应用仅仅开始于过去二十年。当今，数据科学应用已成为一种职业。就像西部开发一样，拥有则无尽的机会，同时也有伴随着很多迷惑与问题。
  本文将从以下部分对机器学习模型的评价进行介绍：
* 介绍模型离线与在线评价体系与知识；
* 介绍一些不同类别下得机器学习模型评价指标，如分类回归、排序等。
* 介绍训练目标、模型验证指标的区别
* 介绍解决数据倾斜的一些方法以及模型参数调优的方法
* 最后介绍一些工具，如GraphLab与Dato等。

机器学习Workflow

  一般的，机器学习过程包括两个阶段，分别为：原型设计阶段（Prototyping）与应用阶段（Deployed），与软件开发类似的Debug与Release阶段。如下图所示：
Prototyping阶段是使用历史数据训练一个适合解决目标任务的一个或多个机器学习模型，并对模型进行验证（Validation）与离线评估（Offline evalutation），然后通过评估指标选择一个较好的模型。如在分类任务中，选择一个适合自己问题的最好的分类算法。Deployed阶段是当模型达到设定的指标值时便将模型上线，投入生产，使用新生成的数据来对该模型进行在线评估（Online evalution），以及使用新数据更新模型。在对模型进行离线评估或者在线评估时，它们所用的评价指标往往不同。如在离线评估中，我们精彩使用的有准确率（accuracy）、精确率－召回率（precision－recall），而在在线评估中，一般使用一些商业评价指标，如用户生命周期值（customer lifetime value）、广告点击率（click through rate）、用户流失率（customer churn rate）等，这些指标才是模型使用者最终关心的一些指标。甚至在对模型进行训练和验证过程中使用的评价指标都不一样。
  同时我们注意到，在这两个阶段使用的数据集也不一样，分别是历史数据（historical data）与新数据（live data）。在机器学习中，很多模型都是假设数据的分布是一定的，不变的，即历史数据与将来的数据都服从相同的分布。但是，在现实生活中，这种假设往往是不成立的，即数据的分布会随着时间的移动而改变，有时甚至变化得很急剧，这种现象称为分布漂移（Distribution Drift）。例如，在文章推荐系统中，文章的主题集数目和主题的发生频率可能是每天改变的，甚至每个小时都在改变，昨天流行的主题在今天可能就不再流行了。如在新闻推荐中，新闻主题就变更得非常快。因此在进行模型构建之时，我们需要去扑捉分布漂移信息并使自己的模型能够应对这种情况。一个常用的方法便是使用一些验证指标对模型在不断新生的数据集上进行性能跟踪。如果指标值能够达到模型构建时的指标值，那么表示模型能够继续对当前数据进行拟合。当性能开始下降时，说明该模型已经无法拟合当前的数据了，因此需要对模型进行重新训练了。
  不同的机器学习任务有着不同的性能评价指标。例如，在垃圾邮件检测系统中，它本身是一个二分类问题（垃圾邮件vs正常邮件），可以使用准确率（Accuracy）、对数损失函数（log-loss）、AUC等评价方法。又如在股票预测中，它本身是一个实数序列数据预测问题，可以使用平方根误差（root mean square error， RMSE）等指标；又如在搜索引擎中进行与查询相关的项目排序中，可以使用精确率－召回率（precision-recall）、NDCG（normalized discounted cumulative gain）。
  正如前面所提到的那样，在原型阶段中最重要的任务便是选择一个正确的适合的模型对数据进行拟合。而当模型训练完毕后，我们需要使用一个与训练数据集独立的新的数据集去对模型进行验证。因为模型本身就是使用训练数据集训练出来的，因此它已经对训练集进行了很好的拟合，但是它在新的数据集上的效果则有待验证，因此需要使用新的与训练集独立的数据集对模型进行训练，确保该模型在新的数据集上也能够满足要求。模型能够对新的数据也能work称为模型的泛化能力。
  那么新的数据集如何得来呢？一般的解决方法是将已有的数据集随机划分成两个个部分，一个用来训练模型，另一个用来验证与评估模型。另一种方法是重采样，即对已有的数据集进行有放回的采样，然后将数据集随机划分成两个部分，一个用来训练，一个用来验证。至于具体的做法有hold-out validation、k-fold cross-validation、bootstrapping与jackknife resampling，后面会进行详细介绍。
  机器学习模型建立过程其实是一个参数学习与调优的过程。对模型进行训练，便是模型参数的学习更新过程。模型出了这些常规参数之外，还存在超参数（hyperparameters）。它们之间有何区别呢？简而言之，模型参数使指通过模型训练中的学习算法而进行调整的，而模型超参数不是通过学习算法而来的，但是同样也需要进行调优。举例，我们在对垃圾邮件检测进行建模时，假设使用logistic回归。那么该任务就是在特征空间中寻找能够将垃圾邮件与正常邮件分开的logistic函数位置，于是模型训练的学习算法便是得到各个特征的权值，从而决定函数的位置。但是该学习算法不会告诉我们对于该任务需要使用多少个特征来对一封邮件进行表征，特征的数目这个参数便是该模型的超参数。
  超参数的调优是一个相当复杂与繁琐的任务。在模型原型设计阶段，需要尝试不同的模型、不同的超参数意见不同的特征集，我们需要寻找一个最优的超参数，因此需要使用相关的搜索算法去寻找，如格搜索（grid search）、随机搜索（random search）以及启发式搜索（smart search）等。这些搜索算法是从超参数空间中寻找一个最优的值。本文后面会进行详细介绍。
  当模型使用离线数据训练好并满足要求后，就需要将模型使用新的在线数据进行上线测试，这就是所谓的在线测试。在线测试不同于离线测试，有着不同的测试方法以及评价指标。最常见的便是A/B testing，它是一种统计假设检验方法。不过，在进行A/B testing的时候，会遇到很多陷阱与挑战，具体会在本文后面进行详细介绍。另一个相对使用较小的在线测试方法是multiarmed bandits。在某些情况下，它比A/B testing的效果要好。后面会进行具体讲解。

评价指标(Evaluation metrics)

  评价指标是机器学习任务中非常重要的一环。不同的机器学习任务有着不同的评价指标，同时同一种机器学习任务也有着不同的评价指标，每个指标的着重点不一样。如分类（classification）、回归（regression）、排序（ranking）、聚类（clustering）、热门主题模型（topic modeling）、推荐（recommendation）等。并且很多指标可以对多种不同的机器学习模型进行评价，如精确率－召回率（precision-recall），可以用在分类、推荐、排序等中。像分类、回归、排序都是监督式机器学习，本文的重点便是监督式机器学习的一些评价指标。

分类评价指标

  分类是指对给定的数据记录预测该记录所属的类别。并且类别空间已知。它包括二分类与多分类，二分类便是指只有两种类别，如垃圾邮件分类中便是二分类问题，因为类别空间只有垃圾邮件和非垃圾邮件这两种，可以称为“负”（negative）与正（positive）两种类别，一般在实际计算中，将其映射到“0”-“1” class中；而多分类则指类别数超过两种。下面主要根据二分类的评价指标进行讲解，不过同时它们也可扩展到多分类任务中。下面对分类中一些常用的评价指标进行介绍。

准确率(Accuracy)

  准确率是指在分类中，使用测试集对模型进行分类，分类正确的记录个数占总记录个数的比例：

accuracy=ncorrectntotal

  准确率看起来非常简单。然而，准确率评价指标没有对不同类别进行区分，即其平等对待每个类别。但是这种评价有时是不够的，比如有时要看类别0与类别1下分类错误的各自个数，因为不同类别下分类错误的代价不同，即对不同类别的偏向不同，比如有句话为“宁可错杀一万，不可放过一千“就是这个道理，例如在病患诊断中，诊断患有癌症实际上却未患癌症（False Positive）与诊断未患有癌症的实际上却患有癌症（False Negative）的这两种情况的重要性不一样。。另一个原因是，可能数据分布不平衡，即有的类别下的样本过多，有的类别下的样本个数过少，两类个数相差较大。这样，样本占大部分的类别主导了准确率的计算，为了解决这个问题，对准确率进行改进，得到平均准确率。

平均准确率(Average Per-class Accuracy)

  为了应对每个类别下样本的个数不一样的情况，对准确率进行变种，计算每个类别下的准确率，然后再计算它们的平均值。举例，类别0的准确率为80%，类别1下的准确率为97.5%，那么平均准确率为(80%+97.5%)/2=88.75%。因为每个类别下类别的样本个数不一样，即计算每个类别的准确率时，分母不一样，则平均准确率不等于准确率，如果每个类别下的样本个数一样，则平均准确率与准确率相等。
  平均准确率也有自己的缺点，比如，如果存在某个类别，类别的样本个数很少，那么使用测试集进行测试时（如k-fold cross validation），可能造成该类别准确率的方差过大，意味着该类别的准确率可靠性不强。

对数损失函数(Log-loss)

  在分类输出中，若输出不再是0-1，而是实数值，即属于每个类别的概率，那么可以使用Log-loss对分类结果进行评价。这个输出概率表示该记录所属的其对应的类别的置信度。比如如果样本本属于类别0，但是分类器则输出其属于类别1的概率为0.51，那么这种情况认为分类器出错了。该概率接近了分类器的分类的边界概率0.5。Log-loss是一个软的分类准确率度量方法，使用概率来表示其所属的类别的置信度。Log-loss具体的数学表达式为：

log_loss=−1N∑i=1Nyilogpi+(1−yi)log(1−pi)

其中， yi 是指第 i 个样本所属的真实类别0或者1， pi 表示第 i 个样本属于类别1的概率，这样上式中的两个部分对于每个样本只会选择其一，因为有一个一定为0，当预测与实际类别完全匹配时，则两个部分都是0，其中假定0log0=0。
  其实，从数学上来看，Log-loss的表达式是非常漂亮的。我们仔细观察可以发现，其信息论中的交叉熵(Cross Entropy，即真实值与预测值的交叉熵)，它与相对熵(Relative Entropy，也称为KL距离或KL散度， Kullback–Leibler divergence.)也非常像。信息熵是对事情的不确定性进行度量，不确定越大，熵越大。交叉熵包含了真实分布的熵加上假设与真实分布不同的分布的不确定性。因此，log-loss是对额外噪声(extra noise)的度量，这个噪声是由于预测值域实际值不同而产生的。因此最小化交叉熵，便是最大化分类器的准确率。

精确率-召回率(Precision-Recall)

  精确率-召回率其实是两个评价指标。但是它们一般都是同时使用。精确率是指分类器分类正确的正样本的个数占该分类器所有分类为正样本个数的比例。召回率是指分类器分类正确的正样本个数占所有的正样本个数的比例。

F1-score：

  F1-score为精确率与召回率的调和平均值，它的值更接近于Precision与Recall中较小的值。即：

F1=2∗precision∗recallprecision+recall

AUC(Area under the Curve(Receiver Operating Characteristic, ROC))

  AUC的全称是Area under the Curve，即曲线下的面积，这条曲线便是ROC曲线，全称为the Receiver Operating Characteristic曲线，它最开始使用是上世纪50年代的电信号分析中，在1978年的“Basic Principles of ROC Analysis ”开始流行起来。ROC曲线描述分类器的True Positive Rate（TPR，分类器分类正确的正样本个数占总正样本个数的比例）与False Positive Rate（FPR，分类器分类错误的负样本个数占总负样本个数的比例）之间的变化关系。如下图所示：

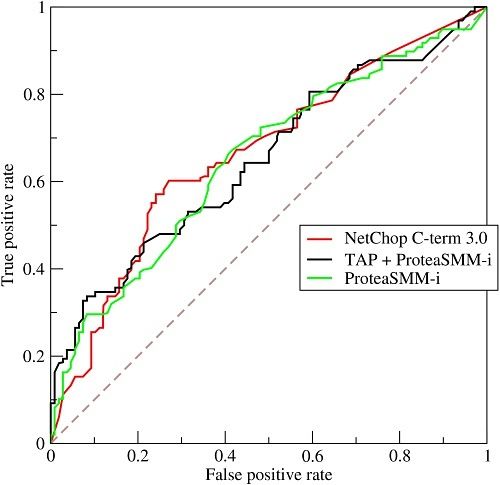
如上图，ROC曲线描述FPR不断变化时，TPR的值，即FPR与TPR之间的关系曲线。显而易见，最好的分类器便是FPR＝0%，TPR＝100%，但是一般在实践中一个分类器很难会有这么好的效果，即一般TPR不等于1，FPR不等于0的。当使用ROC曲线对分类器进行评价时，如果对多个分类器进行比较时，如果直接使用ROC曲线很难去比较，只能通过将ROC分别画出来，然后进行肉眼比较，那么这种方法是非常不便的，因此我们需要一种定量的指标去比较，这个指标便是AUC了，即ROC曲线下的面积，面积越大，分类器的效果越好，AUC的值介于0.5到1.0之间。
  具体如何描绘ROC曲线，如在二分类中，我们需要设定一个阈值，大于阈值分类正类，否则分为负类。因此，我们可以变化阈值，根据不同的阈值进行分类，根据分类结果计算得到ROC空间中的一些点，连接这些点就形成ROC曲线。ROC曲线会经过(0,0)与(1,1)这两点，实际上这两点的连线形成的ROC代表一个随机分类器，一般情况下分类器的ROC曲线会在这条对角连线上方。
  在ROC曲线中，点(0,0)表示TPR＝0，FPR＝0，即分类器将每个实例都预测为负类；点(1,1)表示TPR＝1，FPR＝1，即分类器将每个实例都预测为正类；点(0,0)表示TPR＝1，FPR=0，即分类器将每个正类实例都预测为正类，将每个负类实例都预测为负类，这是一个理想模型。
  ROC曲线有个很好的特性：当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。在实际的数据集中，经常会出现类别不平衡（class imbalance）现象，即负样本比正样本少很多（或者相反），而且测试数据集中的正负样本的分布也可能随时间发生变化。关于ROC与AUC更多的讲解，参见这里。

混淆矩阵(Confusion Matrix)

  混淆矩阵是对分类的结果进行详细描述的一个表，无论是分类正确还是错误，并且对不同的类别进行了区分，对于二分类则是一个2*2的矩阵，对于n分类则是n*n的矩阵。对于二分类，第一行是真实类别为“Positive”的记录个数（样本个数），第二行则是真实类别为“Negative”的记录个数，第一列是预测值为“Positive”的记录个数，第二列则是预测值为“Negative”的记录个数。如下表所示：

	Predicted as Positive	Predicted as Negative
Labeled as Positive	True Positive(TP)	False Negative(FN)
Labeled as Negative	False Positive(FP)	True Negative(TN)

如上表，可以将结果分为四类：
* 真正(True Positive, TP)：被模型分类正确的正样本；
* 假负(False Negative, FN)：被模型分类错误的正样本；
* 假正(False Positive, FP)：被模型分类的负样本；
* 真负(True Negative, TN)：被模型分类正确的负样本；

进一步可以推出这些指标：
* 真正率(True Positive Rate, TPR)，又名灵敏度(Sensitivity)：分类正确的正样本个数占整个正样本个数的比例，即： TPR=TPTP+FN
* 假负率(False Negative Rate, FNR)：分类错误的正样本的个数占正样本的个数的比例，即： FNR=FNTP+FN
* 假正率(False Positive Rate, FPR)：分类错误的负样本个数占整个负样本个数的比例，即： FPR=FPFP+TN
* 真负率(True Negative Rate, TNR)：分类正确的负样本的个数占负样本的个数的比例，即： TNR=TNFP+TN

进一步，由混淆矩阵可以计算以下评价指标：
* 准确率(Accuracy)：分类正确的样本个数占所有样本个数的比例，即：

accuracy=TP+TNTP+FN+FP+TN

* 平均准确率(Average per-class accuracy)：每个类别下的准确率的算术平均，即：

average_accuracy=TPTP+FN+TNTN+FP2

* 精确率(Precision)：分类正确的正样本个数占分类器所有的正样本个数的比例，即：

Precision=TPTP+FP

* 召回率(Recall)：分类正确的正样本个数占正样本个数的比例，即：

Recall=TPTP+FN

* F1-Score：精确率与召回率的调和平均值，它的值更接近于Precision与Recall中较小的值，即：

F1=2∗precision∗recallprecision+recall

* ROC曲线
ROC曲线的x轴便是FPR，y轴便是TPR。

回归评价指标

  与分类不同的是，回归是对连续的实数值进行预测，即输出值是连续的实数值，而分类中是离散值。例如，给你历史股票价格，公司与市场的一些信息，需要你去预测将来一段时间内股票的价格走势。那么这个任务便是回归任务。对于回归模型的评价指标主要有以下几种：
* RMSE
  回归模型中最常用的评价模型便是RMSE（root mean square error，平方根误差），其又被称为RMSD（root mean square deviation），其定义如下：

RMSE=∑ni=0(yi−yi^)2n−−−−−−−−−−−−√

其中， yi 是第 i 个样本的真实值， yi^ 是第 i 个样本的预测值， n 是样本的个数。该评价指标使用的便是欧式距离。
  RMSE虽然广为使用，但是其存在一些缺点，因为它是使用平均误差，而平均值对异常点（outliers）较敏感，如果回归器对某个点的回归值很不理性，那么它的误差则较大，从而会对RMSE的值有较大影响，即平均值是非鲁棒的。
* Quantiles of Errors
  为了改进RMSE的缺点，提高评价指标的鲁棒性，使用误差的分位数来代替，如中位数来代替平均数。假设100个数，最大的数再怎么改变，中位数也不会变，因此其对异常点具有鲁棒性。
  在现实数据中，往往会存在异常点，并且模型可能对异常点拟合得并不好，因此提高评价指标的鲁棒性至关重要，于是可以使用中位数来替代平均数，如MAPE：

MAPE=median(|yi−yi^|/yi)

  MAPE是一个相对误差的中位数，当然也可以使用别的分位数。
* “Almost Crrect” Predictions
  有时我们可以使用相对误差不超过设定的值来计算平均误差，如当 |yi−yi^|/yi 超过100%（具体的值要根据问题的实际情况）则认为其是一个异常点，，从而剔除这个异常点，将异常点剔除之后，再计算平均误差或者中位数误差来对模型进行评价。

排序评价指标

  排序任务指对对象集按照与输入的相关性进行排序并返回排序结果的过程。举例，我们在使用搜索引擎（如google，baidu）的时候，我们输入一个关键词或多个关键词，那么系统将按照相关性得分返回检索结果的页面。此时搜索引擎便是一个排序器。其实，排序也可以说是一个二分类问题。即将对象池中的对象分为与查询词相关的正类与不相关的负类。并且每一个对象都有一个得分，即其属于正类的置信度，然后按照这个置信度将正类进行排序并返回。
  另一个与排序相关的例子便是个性化推荐引擎。个性化推荐引擎便是根据用户的历史行为信息或者元信息计算出每个用户当前有兴趣的项目，并为每个项目赋一个兴趣值，最好按照这个兴趣值进行排序，返回top n兴趣项目。
  对排序器进行评价的一下指标如下：
* Precision-Recall精确率-召回率
  精确率-召回率已经在分类器的评价指标中介绍过。它们同样也可以用于对排序器进行评价。如下图所示：

precision=happy correct answerstotal items returned by ranker

recall=happy correct answerstotal relevant items

  一般的，排序器返回top k的items，如k＝5, 10, 20, 100等。那么该评价指标改为“precision@k”和“recall@k”。
  在推荐系统中，它相当于一个多兴趣查询，即每个用户是一个查询词，然后返回每个查询词相关的top k项目，即返回每个用户感兴趣的top k项目，那么在计算评价指标值时，则需要对每个用户的精确率与召回率进行平均(average precision@k” and “average recall@k”)，将平均值作为模型的精确率与召回率。
* Precision-Recall Curve和F1 Score
  当我们改变top k中的k值时，便可以得到不同的精确率与召回率，那么我们可以通过改变k值而得到精确率曲线和召回率曲线。与ROC曲线一样，我们也需要一个定量的指标对其ROC曲线进行描述而来评价其对应的模型进行评价。可取多个k值，然后计算其评价的精确率与召回率。
  除了Precision-Recall曲线外，另一个便是F1 Score，在分类器评价指标中也有提及到，它将精确度与召回率两个指标结合起来，如下：

F1=2∗precision∗recallprecision+recall

F1-score是精确率与召回率的调和平均值，它的值更接近于Precision与Recall中较小的值。
* NDCG
  在精确率与召回率中，返回集中每个项目的地位（权值）是一样，即位置k处的项目与位置1处的项目地位一样，但是实际情况应该是越排在前面的项目越相关，得分越高。NDCG（normalized discounted cumulative gain）指标便考虑了这种情况，在介绍NDCG之前，首先介绍一下CG(cumulative gain与DCG(discounted cumulative gain)。CG是对排序返回的top k个项目的相关性（即得分）求和，而DCG在每个项目的得分乘上一个权值，该权值与位置成反方向（如成反比），即位置越近，权值越大。而NDCG则对每项的带权值得分先进行归一化，然后再求和。
  在信息检索中或者那些对项目的返回位置关心的模型中经常使用DCG或NDCG。

注意事项

数据倾斜

  在对模型进行评价的时候，数据的好坏往往对评价指标有着很大的影响。其中数据倾斜便是一个常见的数据特征，具体指分类中每个类别的数据量不均衡，相差较大，存在一些异常点，这些异常点会对评价指标的计算产生较大的影响等。

类别不均衡（Imbalanced Classes）

  在前面我们提到使用average per-class accuracy(平均类别准确率)来解决类别不均衡所带来的评价指标问题。举例：假设数据集中正类的数据记录数占总记录数的1%（现实世界中如广告系统中的点击率CTR、推荐系统中的发生行为的用户-项目对、恶意软件检测中的恶意软件），那么这种情况下，如果将所有对象都预测为负类，那么准确率则为99%，然而一个好的分类器准确率应该超过99%。在ROC曲线中，只有左上角的那个部分菜重要，如下图所示：
  如果评价指标对待每一个类别下的每一个实例都采用相等的权值，那么就很难处理类别不平衡问题。因为此时评价指标会被数据量大的类别占主导，起决定性作用。并且不止是影响模型评价阶段，而且会影响模型的训练阶段。如果数据的类别不平衡不做处理，那么就会影响到对小类别的数据记录的分类。
  例如在推荐系统中，真实的数据中，有行为的用户-项目对很少，即大部分用户有发生行为的项目量很少，以及大部分项目只有少量的用户在上面有行为。这两个问题会对推荐系统模型的训练与评价都会产生影响，但训练数据很少时，模型很难学习都用户的偏好，或者项目的兴趣相似项目量很少，导致在对模型进行评价时会得到一个很低的评价指标值，即会得到一个性能较差的推荐模型。

异常点（Outliers）

  异常点是另一种数据倾斜问题。值大的异常点会对回归造成很大的影响与问题。例如，Million Song Dataset中，一个用户对一首歌曲的评分为该用户听这首歌曲的次数，回归模型的预测得分中最高得分竟然超过了16000分，这说明回归模型出现了一些问题，并且导致其它的误差相对于该误差都是极小的。我们可以使用误差的中位数来减少这个异常点所所带来的影响。从而增加鲁棒性。但是该方法不能解决在模型训练阶段的该问题。有效的解决方法是在数据预处理阶段对数据进行数据清洗从而剔除异常点，以及对人物进行重新定义与建模，使得其对异常低能不敏感。

离线评价机制

  在模型的原型设计阶段包：特征选择、模型类型的选择、模型训练等。该部分内容仍然放在模型的原型设计阶段。

模型训练(Training)、验证(Validation)与模型选择(Model Selection)

  我们在解决机器学习任务之时，需要选择一个合适正确的模型去拟合数据，模型的选择发生在模型的验证阶段而不是模型的训练阶段。即当我们训练出多个模型之时，需要选择一个较好的模型，具体而言，便是使用一个新的数据集（称为验证数据集）去对每个模型进行评价，选择一个最优的模型，最优不止是指效果，还有模型复杂度，模型可实践性等方面。如下图所示：
在上图中，超参数调优（hyperparameter tuning ）作为控制模型训练的一个元过程（“meta” process），即前奏过程，将会在后面详细介绍。图中将历史数据集划分成两个部分（一般是随机划分），一个作为模型的训练集，一个作为模型的验证数据集。模型训练阶段使用训练集来训练模型并输出之，然后使用验证集对该模型进行评价。并将验证结果反馈到超参数调优器中，对超参数进行调优后继续训练模型。
   为何要将历史数据划分为两个数据集呢？在统计模型世界中，任何事物的发生都假设是随机的，它们服从一个随机分布。模型便是从随机数据中学习而来的，因此模型也是随机的。并且这个学习的模型需要被一个随机的已观察到的数据集进行测试评估，因此测试结果也是随机的。为了确保准确性与公平性，需要使用一个与训练集独立的数据集对模型进行验证。必须使用与训练样本集不同的数据样本集进行测试，从而可以得到模型的泛化误差。那么如何产生一个新的数据集呢？
  在离线阶段，我们只有一个历史数据集合。那么如何去获得另一个独立的数据集呢？因此我们需要一种机制去产生另一个数据集。一种方式是留下一部分数据来作为验证集，如hold-out validation与cross-validation， 另一种方式是重采样技术，如bootstrapping与Jackknife。如下图所示：
  从上图可以看出，cross-validation与bootstrapping都是将数据集划分为多个较小的数据集，而hold-out validation只是将数据集划分为一大一小的两个部分，大的部分作为训练集，较小的部分作为验证集。

Hold-out Validation

  Hold-out Validation较简单，它假设数据集中的每个数据点都是独立同分布的（i.i.d,independently and identically distributed）。因此我们只需要简单得将原数据集随机划分成两个部分，较大的部分作为训练集，用来训练数据，较小的部分作为验证集，用来对模型进行验证。
  从计算的角度来说，Hold-out Validation是简单的并运行时间快的。缺点便是它是强假设的，缺乏有效的统计特征，并且验证数据集较小，那么其验证的结果则可靠性较低，同时也很难在单个数据集上计算方差信息与置信区间。因此如果需要使用 hold-out validation方法，则需要足够的数据以确保验证集数据足够而确保可靠的统计估计。

Cross-Validation

  Cross-Validation是另一种模型训练集与验证集的产生方法，即将数据集划分成多个小部分集合，如划分成k个部分，那么就变为了k-fold cross validation。依次使用其中的k-1个数据集对模型进行训练（每次使用k-1个不同的数据集），然后使用剩下的一个数据集对模型进行评价，计算评价指标值。接着重复前面的步骤，重复k次，得到k个评价指标值。最后计算这k个评价指标的平均值。其中k是一个超参数，我们可以尝试多个k，选择最好的平均评价指标值所对应的k为最终的k值。
  另一个Cross-Validation的变种便是leave-one-out。该方法与k-fold cross validation方法类似，只是k等于数据集中样本的总数目，即每次使用n-1个数据点对模型进行训练，使用最好一个数据点对模型进行训练。重复n次，计算每次的评价指标值，最后得到平均评价指标值。该方法又称为n-fold cross validation。
  当数据集较小时以致hold-out validation效果较差的时候，cross validation是一种非常有效的训练集-验证集产生方法。

Bootstrapping和Jackknife

  Bootstrapping是一种重采样技术，翻译成自助法。它通过采样技术从原始的单个数据集上产生多个新的数据集，每个新的数据集称为一个bootstrapped dataset，并且每个新的数据集大小与原始数据集大小相等。这样，每个新的数据集都可以用来对模型进行评价，从而可以得到多个评价值，进一步可以得到评价方差与置信区间。
  Bootstrapping与Cross Validation交叉校验相关。Bootstrapping对原数据集进行采样生成一个新的数据集（ bootstrapped dataset）。不同的是，Bootstrapping假设每个数据点都服从均匀分布。它采用的是一种有放回的采样，即将原始数据集通过采样生成一个新的数据集时，每次采样都是有放回得采样，那么这样在新生成的数据集中，可能存在重复的数据点，并且可能会重复多次。
  为什么使用有放回的采样？每一个样本都可以用一个真实的分布进行描述，但是该分布我们并不知道，我们只有一个数据集去推导该分布，因此我们只能用该数据集去估计得到一个经验分布。Bootstrap假设新的样本都是从该经验分布中得到的，即新的数据集服从该经验分布，并且分布一直不变。如果每次采样后不进行放回，那么这个经验分布会一直改变。因此需要进行有放回的采样。
  显然采样后得到的新数据集中会包含同样的样本多次。如果重复采样n次，那么原数据集中的样本出现在新的数据集中的概率为 1−1/e≈63.2% ，用另外一种讲法，原数据集中有约2/3的数据会在新数据集中出现，并且有的会重复多次。
  在对模型进行校验时，可以使用新生成的数据集（ bootstrapped dataset）对模型进行训练，使用未被采样的样本集来对模型进行验证。这种方式类似交叉校验。
  Jackknife翻译成刀切法。Jackknife即从原始进行不放回采样m(m

注意：模型验证与测试不同

  在前面一直都是使用“验证”这个词作为模型训练后需要进行的过程。而没有使用“测试”这个词。因为模型验证与模型测试不同。
  在原型设计阶段中，需要进行模型选择，即需要对多个候选模型在一个或多个验证集上进行性能评价。当在模型训练与验证确定了合适的模型类型（如分类中是采用决策树还是svm等）以及最优的超参数（如特征的个数）后，需要使用全部可利用的数据(包括前面对模型进行验证的验证集)对模型进行训练，训练出的模型便是最终的模型，即上线生产的模型。
  模型测试则发生在模型的原型设计之后，即包含在上线阶段又包含在离线监视（监测分布漂移 distribution drift）阶段。
  不要将训练数据、验证数据与测试数据相混淆。模型的训练、验证与测试应该使用不同的数据集，如果验证数据集、测试数据集与训练数据集有重叠部分，那么会导致模型的泛化能力差。
  就在前一段时间，某队在ImageNet（图像识别最大数据库）图像识别测试挑战赛竞赛宣称自己的效果击败了google和microsoft，图像识别错误率低至4.58%，而microsoft为4.94%，谷歌为4.8%。但是最后查出他们违规了，按照测试的官方规定，参与者每周只能向服务器提交2次测试结果，而他们却在5天内提交了40次结果。此外，ImageNet表示，他们还使用了30个不同的账号，在过去6个月中提交了约200次测试结果。从本质上讲，他们多次测试调优而得到了对测试数据集更好的拟合超参数和模型参数，因此模型的效果可能更好，但是可能会导致过拟合而使得模型的泛化能力差。

总结

  本节主要对模型离线评估与模型离线验证进行讲解。
* 在模型原型设计阶段，需要进行模型选择，包括超参数调优、模型训练、模型验证。
* Cross validation是一种生成训练数据集与验证数据集的机制；该方式在数据集较小时特别有用。
* Hyperparameter tuning是一种为模型选择最优的超参数机制，需要使用交叉校验来对超参数进行评估。
* Hold-out validation是另一种训练数据集与验证集的产生方式，它较简单。当数据集较充分时使用。
* Bootstrapping与Jackknife是两种不同的采样方式，用来产生训练集与验证集。该方法可以为模型提供评价指标值方差与置信区间。

超参数调优(Hyperparameter Tuning)

  在机器学习领域，超参数调优是学习任务的先导步骤（meta），下面将对其进行介绍。

模型参数与超参数

  什么是模型的超参数，它与模型正常的参数有什么不同。机器学习从本质上来说是一个数学模型，它代表着数据的各个方面的联系。
  例如：在线性回归模型中，使用一条线表示特征与目标之间的关系，用数学公式表示为 ：

y=wTx

其中 x 是特征向量，每个样本使用一个特征向量进行表征， y 是一个数值变量，代表目标， w 则是每个特征的权值向量，代表着这条线的斜率。这个模型假设特征与目标之间是线性的。 w 表示模型的参数，需要在模型的训练阶段进行学习更新，也就是说，模型训练其实就是使用一种优化算法决定最优的模型参数来对数据进行拟合。
  另外一种被称为模型超参数。超参数的确定不是在模型的训练阶段。普通的线性回归是没有超参数的（除了特征的个数），而Ridge回归与 Lasso回归都添加了正则项（Ridge岭回归加上L2正则项，Lasso回归加上L1正则项），这些正则项都需要一个正则参数（regularization parameter）。如决策树需要设置树的深度和叶子数、支持向量机（SVM）需要设置一个分类错误的惩罚因子、带核的SVM还需要设置核的参数（如RBF径向基函数的宽度）等。

超参数的作用

   模型的超参数是用来干什么的呢？如正则化因子是来控制模型的能力，模型拟合数据的自由度（degrees of freedom）决定了模型的灵活度。合理的控制模型的能力能够有效得防止过拟合现象。因此为了防止过拟合的发生，需要牺牲一些精度。因此合理的设置模型的超参数则非常重要。
  另一种类型的模型超参数来自于模型的训练阶段。模型训练是一个使损失函数（或代价函数，训练阶段的评价指标）最小化的过程，这过程会用到很多最优化技术与方法，使用的最优化方法中需要用到一些参数。如SGD（ stochastic gradient descent）中，需要一个学习速率因子、初始点以及收敛阈值等。又如，随机森林（Random Forests）和自助提升决策树（Boosted decision trees）需要设置树的个数的参数与正则化参数等等。这些超参数需要被合理地设置以找到一个好的模型。

超参数调优机制

  超参数设置的好坏对模型的评价指标值产生较大的影响。不同的数据集上面创建模型会有不同的最优超参数，因此对于不同的数据集需要各自调优。
  如下图，超参数的设置过程为：首先设置一个初始的超参数值，然后进行模型训练，将模型的指标反馈都超参数调优机制中，调节超参数，继续训练模型，一直进行下去，若干次后得到一个目前最优的超参数值。最后使用该最优的超参数去训练模型，并进行模型验证。

超参数调优算法

  从概念上讲，超参数调优是一个最优化任务过程，就像模型训练一样。然而，这两者之间相当的不同。在模型训练中，使用一个称为代价函数的数据公式为目标去进行对模型参数进行训练调优。而在超参数调优中，无法使用一个形式化的公式为目标去进行调优，它就像一个黑盒子，需要使用模型训练结束后的模型评价结果为指导去进行调优。这就是为什么超参数调优较为困难。下面是一些具体的超参数调优方法：

格搜索(Grid Search)

  顾名思义，格搜索便是将超参数的取值范围划分成一个个格子，然后对每一个格子所对应的值进行评估，选择评估结果最好的格子所对应的超参数值。例如，对于决策树叶子节点个数这一超参数，可以将值划分为这些格子：10, 20, 30, …, 100, …；又如正则化因子这一超参数，一般使用指数值，那么可以划分为：1e-5, 1e-4 1e-3, …, 1。有时可以进行猜测对格子进行搜索去获得最优的超参数。如，当从第一个开始，发现效果较差，第二个好了一点，那么可以第三个可以取最后一个。格搜索较为简单并且可以进行并行化。

随机搜索(Random Search)

  在论文 “Random Search for Hyper Parameter Optimization” (Bergstra and Bengio)中，已经验证了随机搜索是一个简单而有效的方法。它是格搜索的变种。相比于搜索整个格空间，随机搜索只对随机采样的那些格进行计算，然后在这中间选择一个最好的。因此随机搜索比格搜索的代价低。随机搜索有个缺点，即其可能找不到最优的点。但是前面的那篇论文已经证明，随机采样60个点的性能已经足够好了。从概率的角度来说，对于任何的分布的样本空间若存在最大值，那么随机采样60个点中的最大值位于整个样本空间top5%的值的集合中的概率达到95%。证明如下：
  对于top%5的值，我们每次随机采样，得到top5%的值的概率为5%，没有得到top5%的值的概率为(1-0.05)，重复有放回地采样n次，那么至少有一次得到top5的值这件事发生的概率若要超过95%，则：

1−(1−0.05)n>=0.95⇒n>=60

这表示我们只需要从所有候选格中随机采样60个格，便可以以95%的概率得到至少一个的top5%最优的格。因此随机搜索60个格进行计算便可以以很高的概率得到top%5最优的格。当最优格以及近似最优格的集合较大，加上机器学习模型对超参数一个近似最优值与最优值不会太敏感，因此，随机搜索算法便是有效的。由于随机搜索简单并且有效，一般是超参数调优的首选搜索算法。并且其容易并行化。

智能搜索(Smart Search)

  除了前面的两种搜索算法，还可以利用智能搜索算法，但是相对于前面的两种方法，智能搜索算法最大的缺点便是不能并行化。它的处理过程是一个序列，并只处理一部分候选点，然后对当前点进行评估，决定下一个点。智能搜索的目的是只对一部分点进行评估从而节省调优时间。
  可以看出，智能搜索需要时间去计算下一个评估的点，于是相对于前面的方法，可能需要更多的时间。因此只有在对点进行评估所用的时间大于决定下一个需要评估的点的时间时才有意义。当然智能搜索算法也需要自己的超参数，因此也需要调优。有时好的智能搜索算法超参数可以确保智能搜索快于随机搜索。
  文章前面提到，超参数调优是一个困难的过程，因为它不能想模型参数调优那样，给出一个形式化的数学函数，而对数学函数进行调优。因此很多优化算法，如牛顿优化算法、随机梯度下降算法都不能使用。目前有超参数三个智能调优算法：derivative-free optimization, Bayesian optimization和random forest smart tuning。derivative-free优化算法采用启发式来决定下一个计算的点；Bayesian和random forest优化算法都是创建一个响应函数曲面模型，由模型决定下一步需要计算的点。
  Jasper Snoek等使用高斯过程对响应函数进行建模。Frank Hutter等使用回归随机森林来近似这个响应曲面。Misha Bilenko等使用Nelder-Mead来进行超参数调优。

嵌套交叉校验(Nested Cross-Validation)

  嵌套交叉校验又称为嵌套超参数调优。模型选择与超参数调优的不同之处在于：模型选择不仅包括对某个模型的参数进行调优（如决策树的深度），并且包括对不同模型的选择（如分类中，选择决策树还是SVM）。嵌套交叉校验即在进行某个模型训练后，需要对该模型进行交叉校验，然后将结果反馈到超参数调优机制中，对超参数调优，并使用更新后的超参数继续训练模型，一直迭代下去，知道满足一定的要求，同时对其它模型也需要如此进行训练，最后在所有训练好的模型选择一个综合各方面因素最优的模型。

A/B测试的陷阱

   A/B测试（A/B Testing）是机器学习实践中广泛应用的一种方法。但是在应用该方法时，会遇到一些陷阱。下面便对相关问题进行讨论。
  在本文的前部分已经讲述到，机器学习模型的评价分为离线评价与在线评价两个阶段。离线评价阶段发生在模型原型设计阶段，对不同的超参数、不同的特征集、不同模型进行评价，它是一个迭代的过程，使用选定的评价指标对每个迭代过程中生成的模型进行评价。一旦达到指定的迭代次数，则选择所有迭代中最优的模型，作为最终模型并投入到生产环境中使用。而在线评价则是使用一些商业评价指标来对模型进行评价以及更新。而A/B测试则属于在线测试。

什么是A/B测试

  A/B测试是目前在线测试中最主要的方法。该方法可以用来回答“新的模型比旧的模型更好吗（模型）？”、“这个按钮是使用黄色好一些还是蓝色好（设计）”等等问题。在A/B测试中，与两个部分：A和B，或控制/实验（control and experiment），A代表旧模型（设计）的评价，B代表新的模型（设计）的评价，然后将它们进行对比，得到是否新的模型比旧模型更好。当然是由具体的机制来进行衡量。
  该衡量方法便是统计假设检验（statistical hypothesis testing）。其用来回答“新的模型或设计是否对一些关键的评价指标有着大幅度的提升或者明显的提升”。它包括两个对立的假设：空假设（null hypothesis）与替代假设（alternate hypothesis）。前者表示“新的模型或设计没有明显的提升”，后者则表示“新的模型或设计有了明显的提升”，“提升”具体反映在关键评价指标的平均值（mean value）等上面。
  有很多书籍与网上资源对A/B测试有着详细的描述，这里不再累赘。如 www.evanmiller.org，它对A/B测试进行了详细的讲解以及列举了一些工具。简而言之，A/B测试包括以下几个步骤：
* 随机划分成两组A与B
* 使用一些方法分别观察两组中的行为
* 计算一些统计指标
* 计算p-value
* 最后输出孰好孰坏
  举个最简单的例子，在网页设计中使用A/B测试。首先需要建立一个测试页面（experiment page），这个页面可能在标题字体，背景颜色，措辞等方面与原有页面（control page）有所不同，然后将这两个页面以随机的方式同时推送给所有浏览用户。接下来分别统计两个页面的用户转化率，即可清晰的了解到两种设计的优劣。
  A/B测试虽然通俗易懂，但是要想正确的使用它则较为棘手。下面将介绍一些在使用A/B测试时可能会遇到的一些陷阱与问题，这些问题包括理论层面的和实践层面的。

A/B测试的一些陷阱

实验完全分离

  在A/B测试中，需要将用户随机分为两组。一部分用户使用旧的模型或设计（如浏览原来的网页），另一部分用户使用新的模型或设计（如浏览新设计的网页）。那么需要保证experimentation组（使用新的模型或设计的组）的用户的纯净度，什么意思呢？
  A/B测试中，划分为完全独立的，干净的两组是非常重要的。设想一下，在对网页中的按钮新样式进行测试时，需要确保统一用户自始自终是使用同一个按钮设计，那么我们在对用户进行随机划分时，就需要使用能够唯一代表用户的来进行划分（即导流），如用户ID，用户sessions等。Kohavi等的KDD 2012论文表明一些使用旧设计的用户再使用新的设计时会带着某着偏见。

使用什么评价指标

  另一个重要的问题便是，在A/B测试中使用什么评价指标。因为A/B测试是在在线评价阶段，因此使用的评价指标便是商业指标。但是商业指标有没有离线阶段那些评价指标那么容易计算。举个例子，在搜索引擎中，一般对用户的数目、用户在结果站点的逗留时间、以及市场份额。在现实中，统计比较并不是那么容易，因此我们需要对独立用户每天访问数、平均会话时间长度等这些能够反映市场份额的指标进行计算，以便能够对市场份额进行估计。并且一般短期指标并不与长期指标保持一致。
  在机器学习过程中，一般会用到四种类型的评价指标，分别是：训练评价指标（training metrics）、离线评价指标（验证评价指标，offline evaluation metrics or validation metrics）、新生数据评价指标（live metrics）、商业指标（business metrics）。训练评价指标是指模型优化的评价指标，即代价函数（目标函数或损失函数），如在线性回归中使用平方误差和、svm中分类平面几何间隔最大化等。离线评价指标是指模型训练完毕需要使用验证数据集来对模型进行评价，即前面所提到的那些指标，如分类模型评价指标、回归模型评价指标以及排序模型评价指标等。新生数据评价指标即使用模型上线后新生成的数据来评价模型，评价指标同离线评价指标，只是评价所用的数据不同。而商业指标即系统真正关心的最终指标，如转化率、点击率、PV访问量、UV访问量等。每个阶段使用的评价指标不一样，并且这些指标可能并不呈现线性相关，如在回归模型中，随着RMSE的下降，但是点击率（click-through rates.）并没有提高，详细可以参见Kohavi‘s paper。

多少改变才算是真正的改变？

  当确定了使用什么商业指标进行评价以及如何去计算这些指标时，接下来需要明确指标值提升了多少才算正在的提升，即多少的提升才可接受。这在某种程度上取决于实验的观察者数量。并且与问题2一样，它并不是一个数据科学范畴的问题，而是一个商业问题。因此需要根据经验挑选一个合适的值。

单面测试还是双面测试（One-Sided or Two-Sided Test）？

  单面测试只能告诉你新的模型是否比基准的是否更好，而无法告诉你是否更糟。因此需要进行双面测试，其不仅会告诉你新的模型是否会更好并且会告诉你是否更糟。是否更好与是否更糟需要进行分开对待。

多少的FP(False Positives)能够忍受？

  比基准模型更好，但是实际上确不是。FP的代价取决于实际应用。如在医药中，FP意味着病人使用无效药，这样便会对患者的健康造成很大的威胁。又如在机器学习中，FP意味着会使用一个认为会更有效的但却未更有效的模型来代替单前的模型。而FN意味着放弃了一个实际上会更有效的模型。
  统计假设检验可以通过设定显著性水平（ the significance level）控制FP的概率，并通过测试的力（the power of the test.）度来控制FN的概率。
  

需要多少观察者？

  观察者的数量由期望的统计功效（statistical power）部分决定。而统计功效在测试进行之前便需设定。一个常见的尝试时运行测试直到观察到一个重要的结果。这个方法是错误的。测试的力度是能够正确识别那些正样本。它能够使用显著性水平、A组的评价指标值与B组的评价指标值之差、观察者的个数这些去形式化地表示。选择合理的统计功效、显著水平等。然后选择每组中观察者的数量。StitchFix与Evan Miller’s website详细地进行了介绍。
  

评价指标是否满足高斯分布

  A/B测试中绝大部分是使用T检验，但是T检验的所做出的假设前提并不是所有的评价指标都满足的。一个好的方法便是去查看指标的分布与检查T检验所做的假设是否有效。T检验假设是满足高斯分布的，那么评价指标释放满足高斯分布呢？通常，使用中心极限定理可以得到任何独立同分布并且具有期望与方差的随机变量都收敛于高斯分布。不难得出，评价指标假设以下条件成立：
* 指标值是采用平均值
* 指标值的分布是同一分布
* 指标值分布是对称的
但是还是会有一些指标不满足的，如点击率是一个平均值，但是AUC却是一个积分值。并且可能不服从同一分布，如在A/B组中的用户种群不一样。同时，也有可能不是对称的。Kohavi等例举了一些例子说明评价指标不服从高斯分布，在这些例子中，标准误差不会随着测试的进行而降低。比如那些计数评价指标服从负二项式分布。当这些假设不成立时，分布遍不再收敛于高斯分布。
  

方差是否相等

  

p-value意味着什么

  

多模型，多参数

  

测试的时间需要多长

  

分布漂移问题

原文地址：http://www.oreilly.com/data/free/evaluating-machine-learning-models.csp