DFS与BFS详解(很不错的)
有需要关注微信公众号:算法那些事儿
转载至http://www.cnblogs.com/pengyingh/articles/2396432.html 作者July
---------------------
咱们由BFS开始:
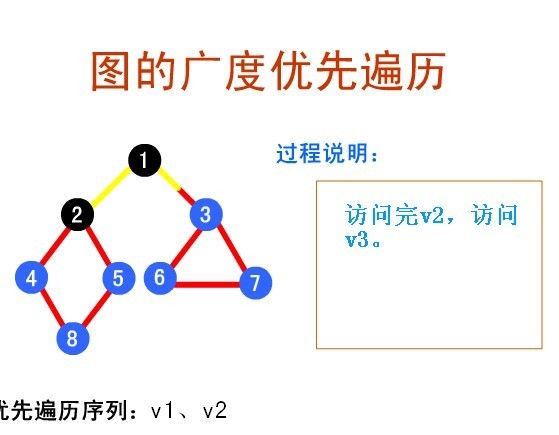
首先,看下算法导论一书关于 此BFS 广度优先搜索算法的概述。
算法导论第二版,中译本,第324页。
广度优先搜索(BFS)
在Prime最小生成树算法,和Dijkstra单源最短路径算法中,都采用了与BFS 算法类似的思想。
//u 为 v 的先辈或父母。
BFS(G, s)
1 for each vertex u ∈ V [G] - {s}
2 do color[u] ← WHITE
3 d[u] ← ∞
4 π[u] ← NIL
//除了源顶点s之外,第1-4行置每个顶点为白色,置每个顶点u的d[u]为无穷大,
//置每个顶点的父母为NIL。
5 color[s] ← GRAY
//第5行,将源顶点s置为灰色,这是因为在过程开始时,源顶点已被发现。
6 d[s] ← 0 //将d[s]初始化为0。
7 π[s] ← NIL //将源顶点的父顶点置为NIL。
8 Q ← Ø
9 ENQUEUE(Q, s) //入队
//第8、9行,初始化队列Q,使其仅含源顶点s。
10 while Q ≠ Ø
11 do u ← DEQUEUE(Q) //出队
//第11行,确定队列头部Q头部的灰色顶点u,并将其从Q中去掉。
12 for each v ∈ Adj[u] //for循环考察u的邻接表中的每个顶点v
13 do if color[v] = WHITE
14 then color[v] ← GRAY //置为灰色
15 d[v] ← d[u] + 1 //距离被置为d[u]+1
16 π[v] ← u //u记为该顶点的父母
17 ENQUEUE(Q, v) //插入队列中
18 color[u] ← BLACK //u 置为黑色
由下图及链接的演示过程,清晰在目,也就不用多说了:
广度优先遍历演示地址:
http://sjjg.js.zwu.edu.cn/SFXX/sf1/gdyxbl.html
-----------------------------------------------------------------------------------------------------------------
ok,不再赘述。接下来,具体讲解深度优先搜索算法。
深度优先探索算法 DFS
//u 为 v 的先辈或父母。
DFS(G)
1 for each vertex u ∈ V [G]
2 do color[u] ← WHITE
3 π[u] ← NIL
//第1-3行,把所有顶点置为白色,所有π 域被初始化为NIL。
4 time ← 0 //复位时间计数器
5 for each vertex u ∈ V [G]
6 do if color[u] = WHITE
7 then DFS-VISIT(u) //调用DFS-VISIT访问u,u成为深度优先森林中一棵新的树
//第5-7行,依次检索V中的顶点,发现白色顶点时,调用DFS-VISIT访问该顶点。
//每个顶点u 都对应于一个发现时刻d[u]和一个完成时刻f[u]。
DFS-VISIT(u)
1 color[u] ← GRAY //u 开始时被发现,置为白色
2 time ← time +1 //time 递增
3 d[u] <-time //记录u被发现的时间
4 for each v ∈ Adj[u] //检查并访问 u 的每一个邻接点 v
5 do if color[v] = WHITE //如果v 为白色,则递归访问v。
6 then π[v] ← u //置u为 v的先辈
7 DFS-VISIT(v) //递归深度,访问邻结点v
8 color[u] <-BLACK //u 置为黑色,表示u及其邻接点都已访问完成
9 f [u] ▹ time ← time +1 //访问完成时间记录在f[u]中。
//完
第1-3行,5-7行循环占用时间为O(V),此不包括调用DFS-VISIT的时间。
对于每个顶点v(-V,过程DFS-VISIT仅被调用依次,因为只有对白色顶点才会调用此过程。
第4-7行,执行时间为O(E)。
因此,总的执行时间为O(V+E)。
下面的链接,给出了深度优先搜索的演示系统:
图的深度优先遍历演示系统:
http://sjjg.js.zwu.edu.cn/SFXX/sf1/sdyxbl.html
===============
最后,咱们再来看深度优先搜索的递归实现与非递归实现
1、DFS 递归实现:
void dftR(PGraphMatrix inGraph)
{
PVexType v;
assertF(inGraph!=NULL,"in dftR, pass in inGraph is null/n");
printf("/n===start of dft recursive version===/n");
for(v=firstVertex(inGraph);v!=NULL;v=nextVertex(inGraph,v))
if(v->marked==0)
dfsR(inGraph,v);
printf("/n===end of dft recursive version===/n");
}
void dfsR(PGraphMatrix inGraph,PVexType inV)
{
PVexType v1;
assertF(inGraph!=NULL,"in dfsR,inGraph is null/n");
assertF(inV!=NULL,"in dfsR,inV is null/n");
inV->marked=1;
visit(inV);
for(v1=firstAdjacent(inGraph,inV);v1!=NULL;v1=nextAdjacent(inGraph,inV,v1))
//v1当为v的邻接点。
if(v1->marked==0)
dfsR(inGraph,v1);
}
2、DFS 非递归实现
非递归版本---借助结点类型为队列的栈实现
联系树的前序遍历的非递归实现:
可知,其中无非是分成“探左”和“访右”两大块访右需借助栈中弹出的结点进行.
在图的深度优先搜索中,同样可分成“深度探索”和“回访上层未访结点”两块:
1、图的深度探索这样一个过程和树的“探左”完全一致,
只要对已访问过的结点作一个判定即可。
2、而图的回访上层未访结点和树的前序遍历中的“访右”也是一致的.
但是,对于树而言,是提供rightSibling这样的操作的,因而访右相当好实现。
在这里,若要实现相应的功能,考虑将每一个当前结点的下层结点中,如果有m个未访问结点,
则最左的一个需要访问,而将剩余的m-1个结点按从左到右的顺序推入一个队列中。
并将这个队列压入一个堆栈中。
这样,当当前的结点的邻接点均已访问或无邻接点需要回访时,
则从栈顶的队列结点中弹出队列元素,将队列中的结点元素依次出队,
若已访问,则继续出队(当当前队列结点已空时,则继续出栈,弹出下一个栈顶的队列),
直至遇到有未访问结点(访问并置当前点为该点)或直到栈为空(则当前的深度优先搜索树停止搜索)。
将算法通过精简过的C源程序的方式描述如下:
//dfsUR:功能从一个树的某个结点inV发,以深度优先的原则访问所有与它相邻的结点
void dfsUR(PGraphMatrix inGraph,PVexType inV)
{
PSingleRearSeqQueue tmpQ; //定义临时队列,用以接受栈顶队列及压栈时使用
PSeqStack testStack; //存放当前层中的m-1个未访问结点构成队列的堆栈.
//一些变量声明,初始化动作
//访问当前结点
inV->marked=1; //当marked值为1时将不必再访问。
visit(inV);
do
{
flag2=0;
//flag2是一个重要的标志变量,用以、说明当前结点的所有未访问结点的个数,两个以上的用2代表
//flag2:0:current node has no adjacent which has not been visited.
//1:current node has only one adjacent node which has not been visited.
//2:current node has more than one adjacent node which have not been visited.
v1=firstAdjacent(inGraph,inV); //邻接点v1
while(v1!=NULL) //访问当前结点的所有邻接点
{
if(v1->marked==0) //..
{
if(flag2==0) //当前结点的邻接点有0个未访问
{
//首先,访问最左结点
visit(v1);
v1->marked=1; //访问完成
flag2=1; //
//记录最左儿子
lChildV=v1;
//save the current node's first unvisited(has been visited at this time)adjacent node
}
else if(flag2==1) //当前结点的邻接点有1个未访问
{
//新建一个队列,申请空间,并加入第一个结点
flag2=2;
}
else if(flag2==2)//当前结点的邻接点有2个未被访问
{
enQueue(tmpQ,v1);
}
}
v1=nextAdjacent(inGraph,inV,v1);
}
if(flag2==2)//push adjacent nodes which are not visited.
{
//将存有当前结点的m-1个未访问邻接点的队列压栈
seqPush(testStack,tmpQ);
inV=lChildV;
}
else if(flag2==1)//only has one adjacent which has been visited.
{
//只有一个最左儿子,则置当前点为最左儿子
inV=lChildV;
}
else if(flag2==0)
//has no adjacent nodes or all adjacent nodes has been visited
{
//当当前的结点的邻接点均已访问或无邻接点需要回访时,则从栈顶的队列结点中弹出队列元素,
//将队列中的结点元素依次出队,若已访问,则继续出队(当当前队列结点已空时,
//则继续出栈,弹出下一个栈顶的队列),直至遇到有未访问结点(访问并置当前点为该点)或直到栈为空。
flag=0;
while(!isNullSeqStack(testStack)&&!flag)
{
v1=frontQueueInSt(testStack); //返回栈顶结点的队列中的队首元素
deQueueInSt(testStack); //将栈顶结点的队列中的队首元素弹出
if(v1->marked==0)
{
visit(v1);
v1->marked=1;
inV=v1;
flag=1;
}
}
}
}while(!isNullSeqStack(testStack));//the algorithm ends when the stack is null
}
-----------------------------
上述程序的几点说明:
所以,这里应使用的数据结构的构成方式应该采用下面这种形式:
1)队列的实现中,每个队列结点均为图中的结点指针类型.
定义一个以队列尾部下标加队列长度的环形队列如下:
struct SingleRearSeqQueue;
typedef PVexType QElemType;
typedef struct SingleRearSeqQueue* PSingleRearSeqQueue;
struct SingleRearSeqQueue
{
int rear;
int quelen;
QElemType dataPool[MAXNUM];
};
其余基本操作不再赘述.
2)堆栈的实现中,每个堆栈中的结点元素均为一个指向队列的指针,定义如下:
#define SEQ_STACK_LEN 1000
#define StackElemType PSingleRearSeqQueue
struct SeqStack;
typedef struct SeqStack* PSeqStack;
struct SeqStack
{
StackElemType dataArea[SEQ_STACK_LEN];
int slot;
};
为了提供更好的封装性,对这个堆栈实现两种特殊的操作
2.1) deQueueInSt操作用于将栈顶结点的队列中的队首元素弹出.
void deQueueInSt(PSeqStack inStack)
{
if(isEmptyQueue(seqTop(inStack))||isNullSeqStack(inStack))
{
printf("in deQueueInSt,under flow!/n");
return;
}
deQueue(seqTop(inStack));
if(isEmptyQueue(seqTop(inStack)))
inStack->slot--;
}
2.2) frontQueueInSt操作用以返回栈顶结点的队列中的队首元素.
QElemType frontQueueInSt(PSeqStack inStack)
{
if(isEmptyQueue(seqTop(inStack))||isNullSeqStack(inStack))
{
printf("in frontQueueInSt,under flow!/n");
return '/r';
}
return getHeadData(seqTop(inStack));
}