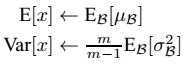深度学习优化策略---炼丹trick之正确使用BN（训练和测试/预测时怎么用）

【深度学习】深入理解Batch Normalization批标准化

一、为什么需要batch normalization

尽管梯度下降法训练神经网络很简单高效，但是需要人为地去选择参数，比如学习率，参数初始化，权重衰减系数，Dropout比例等，而且这些参数的选择对于训练结果至关重要，以至于我们很多时间都浪费到这些调参上。BN算法的强大之处在下面几个方面：

• 可以选择较大的学习率，使得训练速度增长很快，具有快速收敛性。
• 可以不去理会Dropout，L2正则项参数的选择，如果选择使用BN，甚至可以去掉这两项。
• 去掉局部响应归一化层（LRN）。（AlexNet中使用的方法，BN层出来之后这个就不再用了）
• 可以把训练数据打乱，防止每批训练的时候，某一个样本被经常挑选到。（不是很理解啊）

首先来说归一化的问题，神经网络训练开始前，都要对数据做一个归一化处理，归一化有很多好处，原因是网络学习的过程的本质就是学习数据分布，一旦训练数据和测试数据的分布不同，那么网络的泛化能力就会大大降低，另外一方面，每一批次的数据分布如果不相同的话，那么网络就要在每次迭代的时候都去适应不同的分布，这样会大大降低网络的训练速度，这也就是为什么要对数据做一个归一化预处理的原因。另外对图片进行归一化处理还可以处理光照，对比度等影响。
网络一旦训练起来，参数就要发生更新，出了输入层的数据外，其它层的数据分布是一直发生变化的，因为在训练的时候，网络参数的变化就会导致后面输入数据的分布变化，比如第二层输入，是由输入数据和第一层参数得到的，而第一层的参数随着训练一直变化，势必会引起第二层输入分布的改变，把这种改变称之为：Internal Covariate Shift，BN就是为了解决这个问题的。

二、BN基本原理

三、BN算法实现

3、BN与激活函数的结合

根据文献说，BN可以应用于一个神经网络的任何神经元上。
按照原文第一章的理论，应当在每一层的激活函数之后（例如ReLU=max(Wx+b,0)之后），对数据进行归一化。然而，文章中说这样做在训练初期，分界面还在剧烈变化时，计算出的参数不稳定，所以退而求其次，在Wx+b之后进行归一化。因为初始的W是从标准高斯分布中采样得到的，而W中元素的数量远大于x，Wx+b每维的均值本身就接近0、方差接近1，所以在Wx+b后使用Batch Normalization能得到更稳定的结果。

文献主要是把BN变换，置于网络激活函数层的前面。在没有采用BN的时候，激活函数层是这样的：

z=g(Wu+b)

也就是我们希望一个激活函数，比如s型函数s(x)的自变量x是经过BN处理后的结果。因此前向传导的计算公式就应该是：

z=g(BN(Wu+b))

其实因为偏置参数b经过BN层后其实是没有用的，最后也会被均值归一化，当然BN层后面还有个β参数作为偏置项，所以b这个参数就可以不用了。因此最后把BN层+激活函数层就变成了：

z=g(BN(Wu))

四 实际使用(测试与预测)

可能学完了上面的算法，你只是知道它的一个训练过程，一个网络一旦训练完了，就没有了min-batch这个概念了。测试阶段我们一般只输入一个测试样本，看看结果而已。
因此**测试样本前向传导的时候，上面的均值u、标准差σ 要哪里来？**其实网络一旦训练完毕，参数都是固定的，这个时候即使是每批训练样本进入网络，那么BN层计算的均值u、和标准差都是固定不变的。我们可以采用这些训练阶段的均值u、标准差σ来作为测试样本所需要的均值、标准差，于是最后测试阶段的u和σ 计算公式如下：

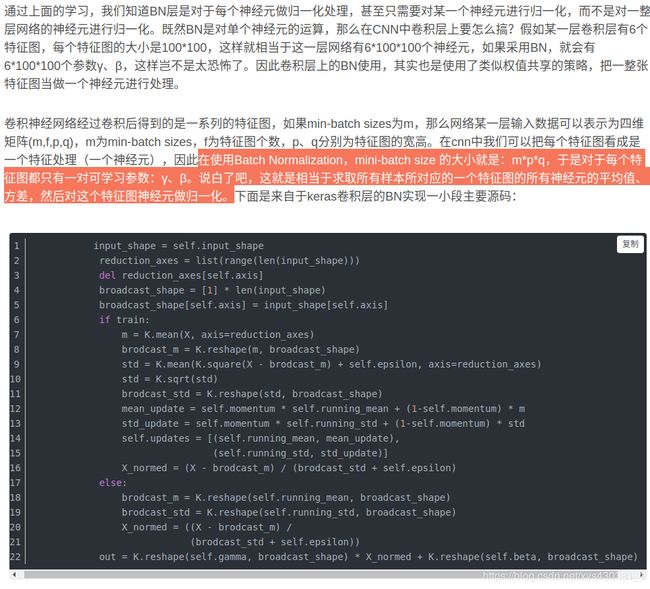
上面简单理解就是：对于均值来说直接计算所有batch u值的平均值；然后对于标准偏差采用每个batch σB的无偏估计。最后测试阶段，BN的使用公式就是：

也就是说， 在test的时候，BN用的是固定的mean和var, 而这个固定的mean和var是通过训练过程中对mean和var进行移动平均得到的，被称之为moving_mean和moving_var。
在实际操作中，每次训练时应当更新一下moving_mean和moving_var，然后把BN层的这些参数保存下来，留作测试和预测时使用。

五、BN在CNN中的应用

示意图与伪代码

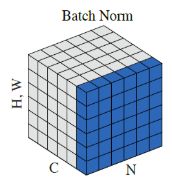
对于同一batch的input，假设输入大小为[batch_num, height, width, channel]，逐channel地计算同一batch中所有数据的mean和variance，再对input使用mean和variance进行归一化，最后的输出再进行线性平移，得到batch_norm的最终结果。伪代码如下：

for i in range(channel):
	x = input[:,:,:,i]
	mean = mean(x)
	variance = variance(x)
	x = (x - mean) / sqrt(variance)
	x = scale * x + offset
	input[:,:,:,i] = x

具体说明

因为batch_norm 在test的时候，用的是固定的mean和var, 而这个固定的mean和var是通过训练过程中对mean和var进行移动平均得到的。而直接使用train_op会使得模型没有计算mean和var，因此正确的方式是：
每次训练时应当更新一下moving_mean和moving_var

那如果在预测时is_traning=false呢，但BN层的参数没有从训练中保存，那使用的就是随机初始化的参数，结果不堪想象。所以需要在训练时把BN层的参数保存下来，然后在预测时加载.

六、tensorflow 中batch_normalization的正确使用姿势

tf.layers.batch_normalization()

BN在如今的CNN结果中已经普遍应用，在tensorflow中可以通过tf.layers.batch_normalization()这个op来使用BN。该op隐藏了对BN的mean var alpha beta参数的显示申明，因此在训练和部署测试中需要特征注意正确使用BN的姿势。
http://www.cnblogs.com/hrlnw/p/7227447.html

说明：
1、需要在来训练中添加update_ops以便在每一次训练完后及时更新BN的参数。
#tf.GraphKeys.UPDATE_OPS ： batch_norm中的moving_mean and moving_variance的更新操作(滑动平均)

2、预测时，需要正确读取BN的参数
与保存类似，读的时候变量也需要为global_variables。如下：
saver = tf.train.Saver()
or saver = tf.train.Saver(tf.global_variables())
saver.restore(sess, ‘here_is_your_personal_model_path’)
PS：预测时还需要把tf.layers.batch_normalization(x, training=is_training,name=scope) 这里的training设为False

https://blog.csdn.net/GAN_player/article/details/77484285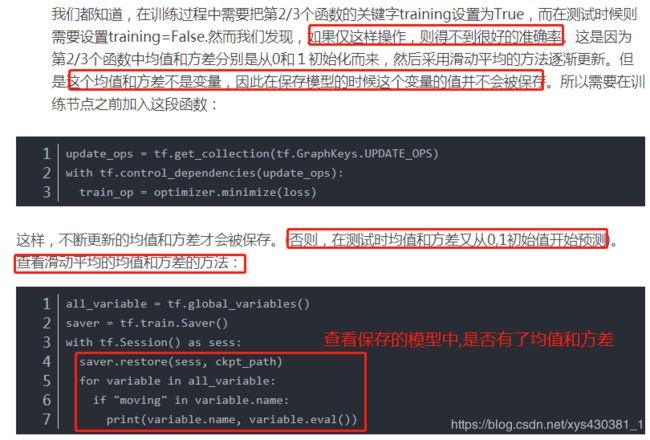

tf.contrib.layers.batch_norm

https://blog.csdn.net/qq_30638831/article/details/82877109

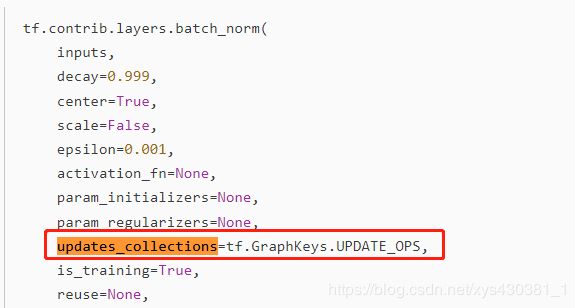
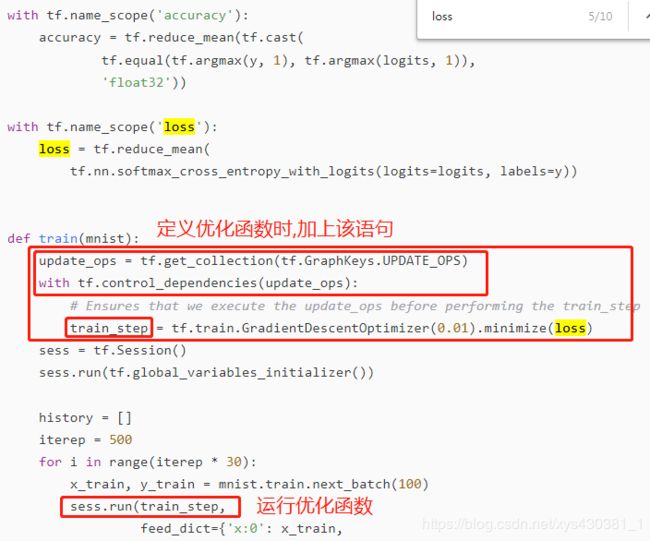
tf.contrib.layers.batch_norm实际代码中的使用

可以将updates_collections = None设置为强制更新，但可能会导致速度损失，尤其是在分布式设置中。

事实上，在DenseNet的实现代码中，都是用的这种方式（updates_collections = None）。


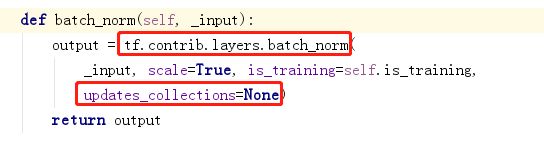
在这两份源代码中，使用batch_norm都是这种方式，而且在整个代码中都找不到如下的关键字：

 update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS)
    with tf.control_dependencies(update_ops)

源代码请参考：
https://github.com/LaurentMazare/deep-models/tree/master/densenet
https://github.com/ikhlestov/vision_networks

七、BN代码实例与效果分析

链接：https://www.jianshu.com/p/ff3768730fb0

这里构建了两个神经神经网络,唯一的区别就是一个进行了BN操作而另外一个没有。

#BN for the first layer input
        if self.norm:
            fc_mean,fc_var = tf.nn.moments(self.xs,axes=[0])
            scale = tf.Variable(tf.ones([1]))
            shift = tf.Variable(tf.zeros([1]))
            epsilon = 0.001
            self.xs = tf.nn.batch_normalization(self.xs,fc_mean,fc_var,shift,scale,epsilon)

接下来是对整个隐层中的处理

def add_layer(self,inputs,in_size,out_size,activation_function=None,norm = False):
        # add layer
        Weights =  tf.Variable(tf.random_normal([in_size,out_size],mean = 0 ,stddev =1))
        biases = tf.Variable(tf.zeros([1,out_size])+0.1)
        Wx_plus_b = tf.matmul(inputs,Weights) + biases
        if norm:
            #compute mean,variance according to the axes
            fc_mean,fc_var = tf.nn.moments(
                Wx_plus_b,
                axes=[0],
            )
            scale = tf.Variable(tf.ones([out_size]))
            shift = tf.Variable(tf.zeros([out_size]))
            epsilon = 0.001 # a smooth value, avoid the value of denominator is zero
            Wx_plus_b =  tf.nn.batch_normalization(Wx_plus_b,fc_mean,fc_var,shift,scale,epsilon)

接下来将两个网络模型的作用进行了可视化处理。

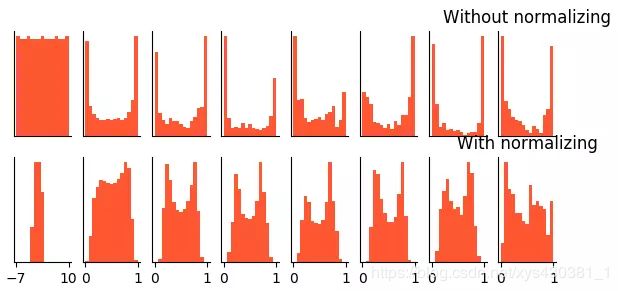
分析上图，初始输入的分布服从均匀分布，可以看出在接收输入时，无BN的模型的输入刚好满足这个分布，但是有BN的模型已经将均匀分布的数据做了标准化处理。可以看出在没有BN的情况下，数据很快就到了激活函数（sigmoid）的饱和区域。但是经过BN处理后，数据中很大一部分处在里激活函数的非饱和区域。
很明显，经过BN处理后的网络收敛的更快。下图显示了两者的loss的变化。

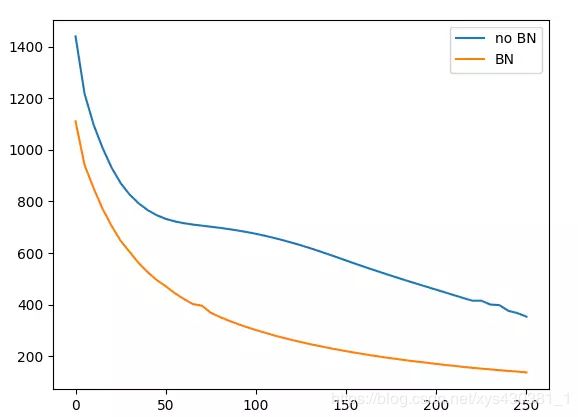
具体的代码链接

参考文献：

深度学习（二十九）Batch Normalization 学习笔记
https://blog.csdn.net/hjimce/article/details/50866313
tensorflow中batch normalization的用法
http://www.cnblogs.com/hrlnw/p/7227447.html
使用tensorflow 的slim模块fine-tune resnet/densenet/inception网络，解决batchnorm问题
https://blog.csdn.net/qq_25737169/article/details/79616671