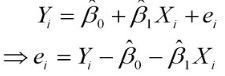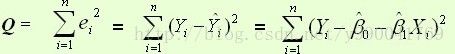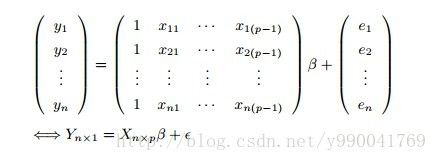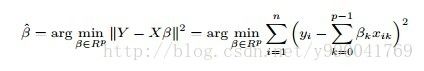线性回归最小二乘法和梯度下降法

问题描述

首先我们定义问题，线性回归要解决的问题就是根据给出的数据学习出一个线性模型。
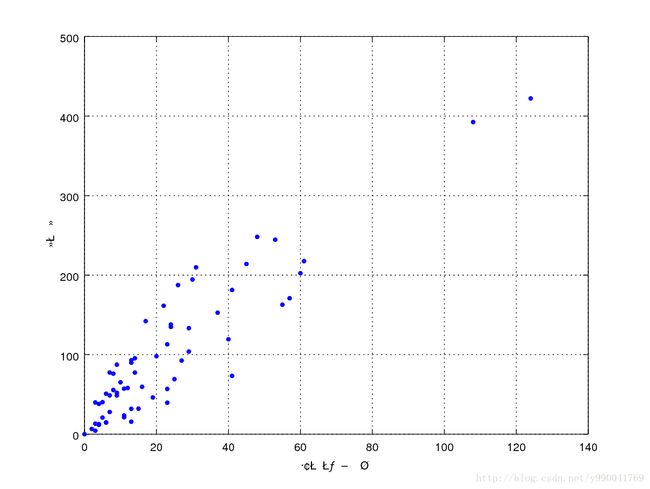
例如我们最常说的身高和体重的关系，以及房屋面积和房价的关系，这里给出一个瑞典汽车保险数据集
数据集 可以直接复制出来用
两列分别表示
索赔要求数量
对所有索赔的总赔付，以千瑞典克朗计
数据前五行

108 392,5
19  46,2
13  15,7
124 422,2
40  119,4

我们按照这个数据集作出图如下

大概观察一下可以用线性模型去定义，现在的问题是根据现有的这个数据集合，我们要学习出一个模型，然后给出索赔要求数量我们能够预测总赔付。
下面给出两种解决方法，并分析这两种方法区别。

最小二乘法

上面这个问题就是最简单的一元线性模型，首先看几个定义
分类问题 监督学习中，如果预测的变量是离散的，我们称其为分类（如决策树，支持向量机等）
回归问题如果预测的变量是连续的，我们称其为回归
一元线性回归分析中，如果只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。
多元线性如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。
对于二维空间线性是一条直线；对于三维空间线性是一个平面，对于多维空间线性是一个超平面

对于上面的数据集，我们可以用多条直线去拟合，那么怎么定义那一条直线是最优呢？

首先定义模型：
其中ei为样本误差

定义损失函数：

上面是损失函数，我们现在目的使得损失函数尽可能的小，就是求如上Q的最小值，函数求极值问题，这里就用到了导数，导数的意义是导数大于0的x处函数递增，导数小于0处x的函数递减，导数为0既为函数的极值点

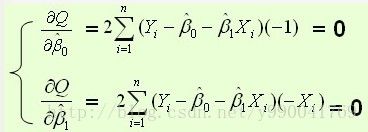
上面x和y都是已知的数据集，β是我们要求的结果，两个函数两个未知数，就可以解方程了。

证明也很简单，这里给个证明的链接,剩下就是几次求和的事儿了。

多元线性回归

首先我们假设模型：

而对于数据集合中n个个体，每个模型有：

表示成矩阵形式：

跟一元的一样，首先我们损失函数：

同样通过求偏导数为0解方程可以得到结果：

梯度下降法

我们要求解的问题和上面一样，同样定义的模型和损失函数都一样，模型为线性模型，损失函数为平方差值和最小，同样这里要求解的是线性方程的参数。

首先我们给每个参数赋值一个随机数，然后按照下面公式进行迭代：

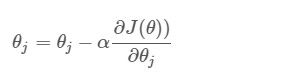
按照最小二乘法，我们直接求出导数为0的点，但是有时候很难解出方程，就考虑使用迭代的方法，首先取一个随机数，然后每一次去想着目标结果逼近，而为了效率最高，我们向着梯度下降最快的方向，既θ在偏导数上的取值。而α是学习速率，是个很重要的参数，设置过大会导致超过最小值，过小则学习的太慢。
对右边的式子展开得到：

则批量梯度下降迭代如下：

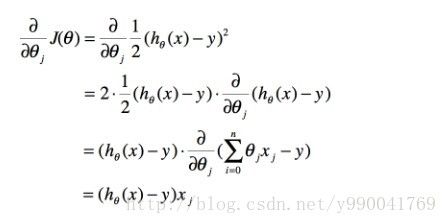
随机梯度下降

上面公式我们发现，每迭代一次我们都要遍历所有的数据去求和，如果数据量大的话可能计算一次很耗时，于是就有了随机梯度下降，这样虽然解决了数据量大的问题，但是学习速度比较曲折，并且学习到的结果可能只是几个局部最优解。如果数据量小建议用批量梯度下降：

首先哦我们看按照批量梯度得到的结果
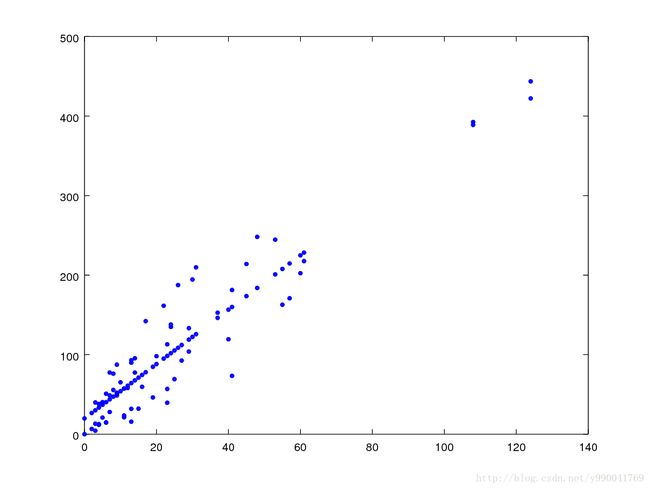
函数为：y = 19.818 + 3.418 * x
做图看一下，看图的话效果还是很不错的

下面给出上面数据的两种方法的代码
批量梯度下降法：

#!/usr/bin/env python
#coding:utf-8

import json
import sys
import time
reload(sys)
sys.setdefaultencoding('utf-8')

if __name__ == "__main__":
    x = [108.0 , 19.0 , 13.0 , 124.0 , 40.0 , 57.0 , 23.0 , 14.0 , 45.0 , 10.0 , 5.0 , 48.0 , 11.0 , 23.0 , 7.0 , 2.0 , 24.0 , 6.0 , 3.0 , 23.0 , 6.0 , 9.0 , 9.0 , 3.0 , 29.0 , 7.0 , 4.0 , 20.0 , 7.0 , 4.0 , 0.0 , 25.0 , 6.0 , 5.0 , 22.0 , 11.0 , 61.0 , 12.0 , 4.0 , 16.0 , 13.0 , 60.0 , 41.0 , 37.0 , 55.0 , 41.0 , 11.0 , 27.0 , 8.0 , 3.0 , 17.0 , 13.0 , 13.0 , 15.0 , 8.0 , 29.0 , 30.0 , 24.0 , 9.0 , 31.0 , 14.0 , 53.0 , 26.0 ]
    y = [392.5 , 46.2 , 15.7 , 422.2 , 119.4 , 170.9 , 56.9 , 77.5 , 214.0 , 65.3 , 20.9 , 248.1 , 23.5 , 39.6 , 48.8 , 6.6 , 134.9 , 50.9 , 4.4 , 113.0 , 14.8 , 48.7 , 52.1 , 13.2 , 103.9 , 77.5 , 11.8 , 98.1 , 27.9 , 38.1 , 0.0 , 69.2 , 14.6 , 40.3 , 161.5 , 57.2 , 217.6 , 58.1 , 12.6 , 59.6 , 89.9 , 202.4 , 181.3 , 152.8 , 162.8 , 73.4 , 21.3 , 92.6 , 76.1 , 39.9 , 142.1 , 93.0 , 31.9 , 32.1 , 55.6 , 133.3 , 194.5 , 137.9 , 87.4 , 209.8 , 95.5 , 244.6 , 187.5]
    print len(x),len(y)
    epsilon = 0.0001  #迭代伐值

    cnt = 0
    alpha = 0.001
    theta0 = 0
    theta1 = 0

    error1 = 0
    error0 = 0
    while True:
        sum0 = 0 
        sum1 = 0
        cnt = cnt + 1
        for i in range(0, len(x)):
            diff =y[i] - (theta0 + theta1 * x[i])

            sum0 = sum0 + diff
            sum1 = sum1 + diff * x[i]

        theta0 = theta0 + alpha * sum0 / len(x)
        theta1 = theta1 + alpha * sum1 / len(x)

        error1 = 0
        for i in range(0, len(x)):
            error1 = error1 + (y[i] - (theta0 + theta1 * x[i] )) ** 2

        if abs(error1 - error0) < epsilon:
            break
        else:
            error0 = error1

        print 'thata0 : %f, thata1 :%f error1 : %f' % (theta0, theta1, error1)

这一份数据用随机梯度搞不定，学习不出比较好的结果，考虑是不是对数据做一些预处理
随机梯度下降法：

#!/usr/bin/env python
#coding:utf-8

import json
import sys
import time
reload(sys)
sys.setdefaultencoding('utf-8')

if __name__ == "__main__":
    x = [108.0 , 19.0 , 13.0 , 124.0 , 40.0 , 57.0 , 23.0 , 14.0 , 45.0 , 10.0 , 5.0 , 48.0 , 11.0 , 23.0 , 7.0 , 2.0 , 24.0 , 6.0 , 3.0 , 23.0 , 6.0 , 9.0 , 9.0 , 3.0 , 29.0 , 7.0 , 4.0 , 20.0 , 7.0 , 4.0 , 0.0 , 25.0 , 6.0 , 5.0 , 22.0 , 11.0 , 61.0 , 12.0 , 4.0 , 16.0 , 13.0 , 60.0 , 41.0 , 37.0 , 55.0 , 41.0 , 11.0 , 27.0 , 8.0 , 3.0 , 17.0 , 13.0 , 13.0 , 15.0 , 8.0 , 29.0 , 30.0 , 24.0 , 9.0 , 31.0 , 14.0 , 53.0 , 26.0 ]
    y = [392.5 , 46.2 , 15.7 , 422.2 , 119.4 , 170.9 , 56.9 , 77.5 , 214.0 , 65.3 , 20.9 , 248.1 , 23.5 , 39.6 , 48.8 , 6.6 , 134.9 , 50.9 , 4.4 , 113.0 , 14.8 , 48.7 , 52.1 , 13.2 , 103.9 , 77.5 , 11.8 , 98.1 , 27.9 , 38.1 , 0.0 , 69.2 , 14.6 , 40.3 , 161.5 , 57.2 , 217.6 , 58.1 , 12.6 , 59.6 , 89.9 , 202.4 , 181.3 , 152.8 , 162.8 , 73.4 , 21.3 , 92.6 , 76.1 , 39.9 , 142.1 , 93.0 , 31.9 , 32.1 , 55.6 , 133.3 , 194.5 , 137.9 , 87.4 , 209.8 , 95.5 , 244.6 , 187.5]
    print len(x),len(y)
    epsilon = 0.0001  #迭代伐值

    cnt = 0
    alpha = 0.01
    theta0 = 0
    theta1 = 0

    error1 = 0
    error0 = 0
    while True:
        cnt = cnt + 1
        for i in range(0, len(x)):
            diff =y[i] - (theta0 + theta1 * x[i])

            theta0 = theta0 + alpha * diff 
            theta1 = theta1 + alpha * diff * x[i]

            error1 = 0
            for i in range(0, len(x)):
                error1 = error1 + (y[i] - (theta0 + theta1 * x[i] )) ** 2

            if abs(error1 - error0) < epsilon:
                break
            else:
                error0 = error1

            print 'thata0 : %f, thata1 :%f error1 : %f' % (theta0, theta1, error1)