BERT基础(一):self_attention自注意力详解
BERT中的主要模型为Transformer,而Transformer的主要模块就是self-attention。为了更好理解bert,就从最基本的self-attention 开始。之后的博文则一步一步推进到bert。
参考:李宏毅2019年新增课程 week 15 transformer 课程笔记
视频及课件地址:https://www.bilibili.com/video/av65521101/?p=97
一、RNN和CNN的局限
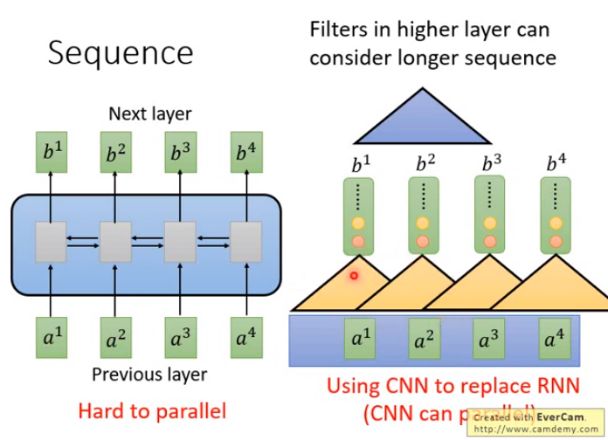
RNN的输入是一串vector sequence,输出是另外一串vector sequence。如果是单向的RNN,输出是 b 4 b^4 b4的时候,会把 a 1 a^1 a1到 a 4 a^4 a4通通都看过,输出 b 3 b^3 b3的时候,会把 a 1 a^1 a1到 a 3 a^3 a3都看过。如果是双向RNN,输出每一个 b 1 b^1 b1到 b 4 b^4 b4的时候,已经把整个input sequence通通都看过。
RNN存在的问题是不容易被平行化,即假设单向的情况下要算出 b 4 b^4 b4,需要先看 a 1 a^1 a1再看 a 2 、 a 3 、 a 4 a^2、a^3、a^4 a2、a3、a4才能算出。
解决方法:用CNN代替RNN。如图,input一个sequence a 1 a^1 a1到 a 4 a^4 a4,每一个三角形代表一个filter(滤波器),输入是sequence 中的一小段,输出一个数值。若有一堆filter,输入是一个sequence,输出是另外的sequence。
CNN也有办法考虑更长的资讯,只要叠加很多层,上层的filter就可以考虑比较多的资讯。举例来说,叠了第一层CNN再叠第二层的CNN,第二层CNN的filter 会把第一层的output当作input。如图,蓝色的filter由 b 1 , b 2 , b 3 b^1,b^2,b^3 b1,b2,b3决定输出,而 b 1 , b 2 , b 3 b^1,b^2,b^3 b1,b2,b3是由来 a 1 a^1 a1到 a 4 a^4 a4决定他们的输出,所以等同于蓝色的filter 已经看到了 a 1 a^1 a1到 a 4 a^4 a4的内容。CNN的好处是可以平行化,每一个同颜色的filter可以同时计算。
CNN 的缺点:每一个CNN只能考虑非常有限的内容,要叠很多层才能看到长期资讯。
二、 self-Attention
假设我们想用机器翻译的手段将下面这句话翻译成中文:
“The animal didn’t cross the street because it was too tired”
“The animal didn’t cross the street because it was too wide”
当机器读到“it”时,“it”代表“animal”还是“street”呢?对于人类来讲,这是一个极其简单的问题,但是对于机器或者说算法来讲却十分不容易。
self-Attention则是处理此类问题的一个解决方案,当模型处理到“it”时,self-Attention可以将“it”和“animal‘联系到一起。
它是怎么做到的呢?
通俗地讲,当模型处理一句话中某一个位置的单词时,self-Attention允许它看一看这句话中其他位置的单词,看是否能够找到能够一些线索,有助于更好地表示(或者说编码)这个单词。
1. self-Attention优势
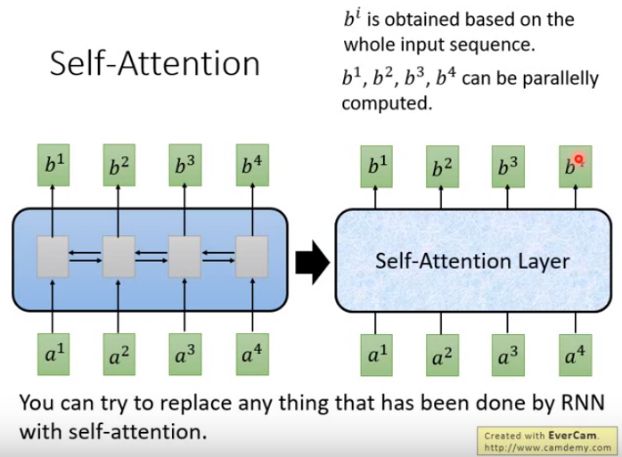
Self-Attention:输入和输出都是sequence,跟Bi-RNN有同样的能力,每个输出都看过input sequence,但特别的地方是 b 1 b^1 b1到< b 4 b^4 b4可以并行计算。
self-Attention这个概念最早出现在谷歌的论文 Attention is all you need,意思是不需要CNN也不需要RNN,唯一需要的就是attention。
2. self-Attention具体推导过程
如图:
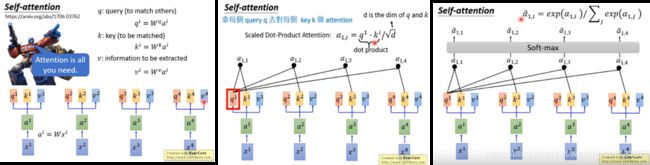
(1) x 1 x^1 x1到 x 4 x^4 x4是 i n p u t s e q u e n c e input sequence inputsequence,每一个 i n p u t input input通过 e m b e d d i n g embedding embedding 乘上一个矩阵,变成 a 1 a^1 a1到 a 4 a^4 a4:
a i = W x i a^i=Wx_i ai=Wxi
(2)每一个 a i a^i ai上分别乘上3个不同的transformation产生三个 v e c t o r vector vector。 q ( q u e r y ) q(query) q(query)指和其他项作匹配, k ( k e y ) k(key) k(key)指被匹配项, v ( v a l u e ) v(value) v(value)是被取出来的信息。此中三个向量的维度一致。
q i = W q a i q^i=W^qa^i qi=Wqai
k i = W k a i k^i=W^ka^i ki=Wkai
v i = W v a i v^i=W^va^i vi=Wvai
(3)拿每个 q q q 去对每一个 k k k做attention,attention 有各式各样的算法,本质是将两个向量合成一个数值,此处用了原始paper的方法。具体方法:
拿 q 1 q^1 q1对 k 1 k^1 k1到 k 4 k^4 k4做attention得到 α 1 , 1 \alpha_{1,1} α1,1到 α 1 , 4 \alpha_{1,4} α1,4,在self-attention layer里面attention算法用的是 scaled dot-product (点乘:求出两个向量的相似性)attention:
α 1 , i = q 1 . k i / d \alpha_{1,i}=q^1.k^i/\sqrt{d} α1,i=q1.ki/d
其中 d d d 为向量 q q q 和 v v v 的 维度,直观解释公式中除以 d \sqrt{d} d 是因为 q q q 和 k k k 做dot product的数值会随着维度的增加而增大,为了把注意力矩阵变成标准正态分布,使得softmax归一化后的结果更加稳定,以便反向传播的时候获取平衡的梯度。
此处提一下点积的集合意义:两个向量越相似,他们的点积就越大,否则越小。
(4)把 α 1 , 1 \alpha_{1,1} α1,1到 α 1 , 4 \alpha_{1,4} α1,4通过softmax归一化得到 α ^ 1 , 1 \hat{\alpha}_{1,1} α^1,1到 α ^ 1 , 4 \hat{\alpha}_{1,4} α^1,4。
α ^ 1 , i = e x p ( α 1 , i ) / ∑ j e x p ( α 1 , i ) \hat{\alpha}_{1,i}=exp(\alpha_{1,i})/\sum_j{exp(\alpha_{1,i})} α^1,i=exp(α1,i)/j∑exp(α1,i)
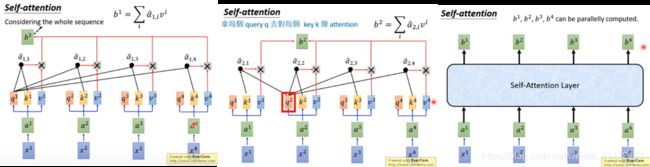
(5)把 v 1 v^1 v1到 v 4 v^4 v4和 α ^ 1 , 1 \hat{\alpha}_{1,1} α^1,1到 α ^ 1 , 4 \hat{\alpha}_{1,4} α^1,4分别相乘再相加,得到sequence的第一个输出向量 b 1 b^1 b1。
可以注意到,产生 b 1 b^1 b1的时候用了 v 1 v^1 v1到 v 4 v^4 v4的 w e i g h t e d s u m weighted sum weightedsum;而 v 1 v^1 v1到 v 4 v^4 v4由 α 1 , 1 \alpha_{1,1} α1,1到 α 1 , 4 \alpha_{1,4} α1,4做 t r a n s f o r m a t i o n transformation transformation得到,所以相当于产生 b 1 b^1 b1的时候看了 α 1 , 1 \alpha_{1,1} α1,1到 α 1 , 4 \alpha_{1,4} α1,4。如果产生 b 1 b^1 b1的时候不想考虑整个句子的资讯,只想考虑 l o c a l local local的 i n f o r m a t i o n information information,可以让远的 α ^ 1 , 1 \hat{\alpha}_{1,1} α^1,1到 α ^ 1 , 4 \hat{\alpha}_{1,4} α^1,4的值变为0;如果考虑 g l o b a l global global的 i n f o r m a t i o n information information,让 α ^ 1 , 3 \hat{\alpha}_{1,3} α^1,3到 α ^ 1 , 4 \hat{\alpha}_{1,4} α^1,4有值就可以。
(6)重复以上的步骤计算出 b 2 , b 3 , b 4 b^2,b^3,b^4 b2,b3,b4, s e l f − a t t e n t i o n l a y e r self-attention layer self−attentionlayer做的事情和RNN是一样的,与RNN 不同的是, b 1 b^1 b1到 b 4 b^4 b4可以平行的计算出来。
三、Multi-head self-attention (多头注意力)
为什么是多头呢?因为我们要用注意力机制来提取多重语意的含义。
原理:每个 a i a^i ai都会得到 q i , k i , v i q^i,k^i,v^i qi,ki,vi,在2头的情况下,把 q i q^i qi进一步分裂得到 q i , 1 q^{i,1} qi,1和 q i , 2 q^{i,2} qi,2,把 k i k^i ki和 v i v^i vi也进行分裂。接下来做 s e l f − a t t e n t i o n self-attention self−attention,只是 q i , 1 q^{i,1} qi,1只会对 k i , 1 , k j , 1 k^{i,1},k^{j,1} ki,1,kj,1即跟它同样是第一个的 v e c t o r vector vector做 d o t p r o d u c t dot product dotproduct(点积),然后计算出 b i , 1 , q i , 2 b^{i,1},q^{i,2} bi,1,qi,2只会对 k i , 2 , k j , 2 k^{i,2},k^{j,2} ki,2,kj,2做attention得到 b i , 2 b^{i,2} bi,2,然后把 b i , 1 b^{i,1} bi,1和 b i , 2 b^{i,2} bi,2连接起来。可以对连接起来的向量乘上一个 t r a n s f o r m transform transform做降维得到最终的输出 b i b^i bi。
多头的好处是不同的head关注的点不一样。举例来说,有的 h e a d head head关注 l o c a l local local的资讯,有的 h e a d head head关注比较长时间的资讯,比较 g l o b a l global global的资讯,有了 m u l t i − h e a d multi-head multi−head之后,每个 h e a d head head会各司其职,做自己想做的事情。
公式表达:
四、self-attention的局限性
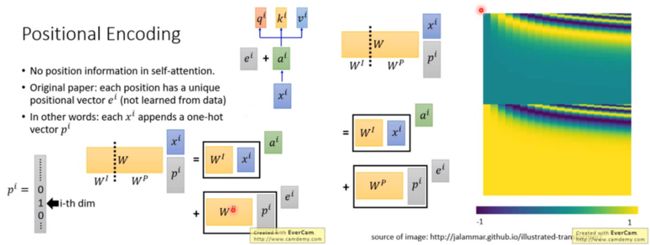
对self-attention来说,它跟每一个input vector都做attention,所以没有考虑到input sequence的顺序。而我们希望考虑input sequence的顺序。所以在原始paper里,每一个input x i x^i xi通过transform 变成 a i a^i ai以后还要加上一个维度相同的向量 e i e^i ei, e i e^i ei是手设的,代表位置的资讯。
换一种说法就是,在 i n p u t input input x i x^i xi后连接一个 o n e − h o t v e c t o r one-hot vector one−hotvector p i p^i pi, p i p^i pi代表位置资讯,第 i i i维是1,其他维是0。连接之后乘上一个矩阵 W W W做 t r a n s f o r m transform transform, W W W可以拆成 W I W^I WI和 W P W^P WP,把 W I W^I WI跟 x i x^i xi相乘得到 a i a^i ai, W p W^p Wp跟 P i P^i Pi相乘得到 e i e^i ei。 W P W^P WP是可以通过学习得到的,论文里面 W P W^P WP是人手设的。
五、总结
self—attention最终要得到的结果总结为:
A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d k ) V Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V Attention(Q,K,V)=softmax(dkQKT)V
其含义是用注意力权重对已用数学表达的字向量进行加权线性组合,从而使每个字向量都含有当前句子内所有字向量的信息。
位置嵌入的内容将在transformer 中讲到: