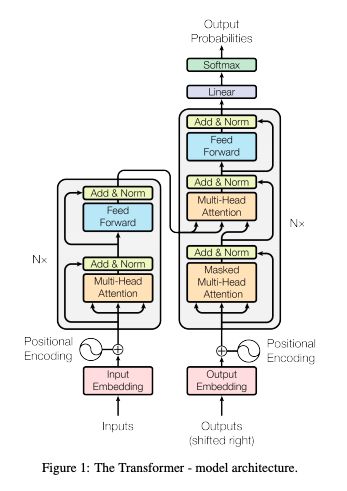
BERT基础(二):Transformer 详解
Transformer 中 self - attention 的详解参考:
BERT基础(一):self_attention自注意力详解
在 Transformer 之前,多数基于神经网络的机器翻译方法依赖于循环神经网络(RNN),后者利用循环(即每一步的输出馈入下一步)进行顺序操作(例如,逐词地翻译句子)。尽管 RNN 在建模序列方面非常强大,但其序列性意味着该网络在训练时非常缓慢,因为长句需要的训练步骤更多,其循环结构也加大了训练难度。与基于 RNN 的方法相比,Transformer 不需要循环,而是并行处理序列中的所有单词或符号,同时利用自注意力机制将上下文与较远的单词结合起来。通过并行处理所有单词,并让每个单词在多个处理步骤中注意到句子中的其他单词。
下面就细致理解一下Transformer的模型结构,理解每一步在做什么。
0. 总体结构
- 先把Transformer想象成一个黑匣子,在机器翻译的领域中,这个黑匣子的功能就是输入一种语言然后将它翻译成其他语言。如下图:
![]()
- 这个黑匣子由2个部分组成,一个Encoders和一个Decoders。
![]()
- 对这个黑匣子进一步的剖析,发现每个Encoders中分别由6个Encoder组成(论文中是这样配置的)。而每个Decoders中同样也是由6个Decoder组成。
![]()
- 对于Encoders中的每一个Encoder,他们结构都是相同的,但是并不会共享权值。每层Encoder有2个部分组成,如下图:
![]()
Self-attention的输出会被传入一个全连接的前馈神经网络,每个encoder的前馈神经网络参数个数都是相同的,但是他们的作用是独立的。
- 每个Decoder也同样具有这样的层级结构,但是在这之间有一个Attention层,帮助Decoder专注于与输入句子中对应的那个单词。
![]()
1. Positional Encoding
使用Self-Attention方式进行编码时无法处理以下的顺序问题:
我从北京到上海
我从上海到北京
上述两个语句进行编码时,第一句的北京与上海两个词的编码与第二句的北京与上海两个词的编码会完全相同,但这两个语句中的两个地点代表着不同的含义:起始位置、终点位置。为了解决此问题,进行自编码时在输入层引入了一个位置编码,如下所示:
P E ( p o s , 2 i ) = s i n ( p o s 1000 0 2 i / d m o d e l ) {PE}_{(pos,2i)}=sin(\frac {pos}{10000^{2i/d_{model}}}) PE(pos,2i)=sin(100002i/dmodelpos)
P E ( p o s , 2 i + 1 ) = c o s ( p o s 1000 0 2 i / d m o d e l ) {PE}_{(pos,2i+1)}=cos(\frac {pos}{10000^{2i/d_{model}}}) PE(pos,2i+1)=cos(100002i/dmodelpos)
与输入的计算过程:拼接
X = E m b e d d i n g L o o k u p ( X ) + P o s i t i o n a l E n c o d i n g ( t ) X=EmbeddingLookup(X)+PositionalEncoding(t) X=EmbeddingLookup(X)+PositionalEncoding(t)
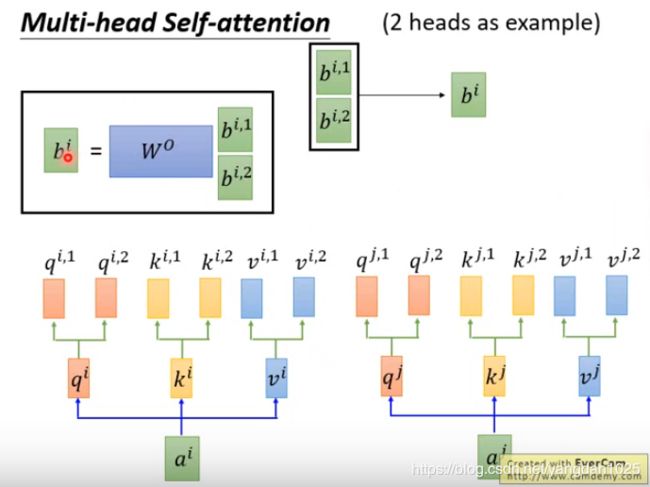
2. self-attention
q i = W q a i q^i=W^qa^i qi=Wqai
k i = W k a i k^i=W^ka^i ki=Wkai
v i = W v a i v^i=W^va^i vi=Wvai
A t t e n t i o n ( Q , K , V = s o f t m a x ( Q K T d k ) V Attention(Q,K,V=softmax(\frac{QK^T}{\sqrt{d_k}})V Attention(Q,K,V=softmax(dkQKT)V
![]()
- Multi-head
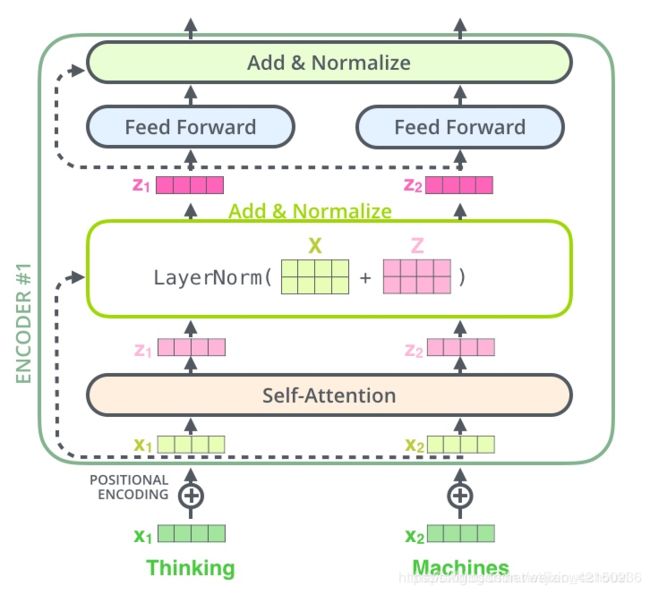
3. Layer Normalization和残差连接
(1) 残差连接
我们在上一步得到了经过注意力矩阵加权后的V,也就是 A t t e n t i o n ( Q , K , V ) Attention(Q,K,V) Attention(Q,K,V), 对它进行转置(图中的Z),使其和 X e m b e d d i n g X_{embedding} Xembedding的维度一致,然后把它们加起来做残差连接,直接进行元素相加,因为他们的维度一致。
X e m b e d d i n g + A t t e n t i o n ( Q , K , V ) X_{embedding}+Attention(Q,K,V) Xembedding+Attention(Q,K,V)
(2)LayerNorm
作用是把神经网络中隐藏层归一化为标准正态分布,以起到加快训练速度,加速收敛的作用:
- 上式中以矩阵的行(row)为单位求均值:
μ i = 1 m ∑ i = 1 m x i j \mu_i=\frac1m\sum^m_{i=1}x_{ij} μi=m1i=1∑mxij
- 上式中以矩阵的行(row)为单位求方差:
σ j 2 = 1 m ∑ i = 1 m ( x i j − μ j ) 2 \sigma_j^2=\frac1m\sum^m_{i=1}(x_{ij}-\mu_j)^2 σj2=m1i=1∑m(xij−μj)2
- 然后用每一行的每一个元素减去这行的均值,再除以这行的标准差,从而得到归一化以后的数值:
L a y e r N o r m ( x ) = α ∗ x i j − μ i σ i 2 + ϵ + β LayerNorm(x)=\alpha*\frac{x_{ij}-\mu_i}{\sqrt{\sigma_i^2+\epsilon}}+\beta LayerNorm(x)=α∗σi2+ϵxij−μi+β
式中的 ϵ \epsilon ϵ是为了防止除0;之后引入两个可训练参数 α 、 β \alpha、\beta α、β 来弥补归一化过程中损失掉的信息。此处一般初始化 α \alpha α为全1,而 β \beta β 为全0。
最后输出 :(X为输入词向量, X a t t e n t i o n X_{attention} Xattention为self-attention输出序列)
X a t t e n t i o n = X + X a t t e n t i o n X_{attention}=X+X_{attention} Xattention=X+Xattention
X a t t e n t i o n = L a y e r N o r m ( X a t t e n t i o n ) X_{attention}=LayerNorm(X_{attention}) Xattention=LayerNorm(Xattention)
4. Feed Forward
两层线性映射并用激活函数激活,比如ReLU:
X h i d d e n = A c t i v a t e ( L i n e a r ( L i n e a r ( X a t t e n t i o n ) ) ) X_{hidden}=Activate(Linear(Linear(X_{attention}))) Xhidden=Activate(Linear(Linear(Xattention)))
ReLU :
f ( x ) = m a x ( 0 , x ) f(x)=max(0,x) f(x)=max(0,x)
5. Encoder和Decoder之间的信息交互
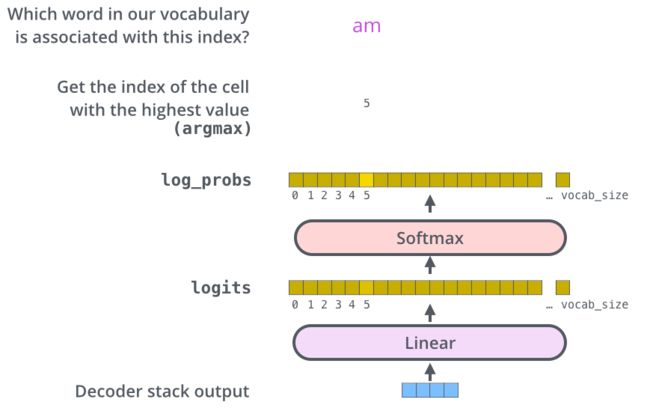
解码器最后输出的是一个向量,如何把它变成一个单词,这就要靠它后面的线性层和 softmax 层
线性层是一个简单的全连接神经网络,它是由Decoder堆栈产生的向量投影到一个更大,更大的向量中,称为对数向量;
在线性层之后是一个softmax层,softmax将这些分数转换为概率。选取概率最高的索引,然后通过这个索引找到对应的单词作为输出。