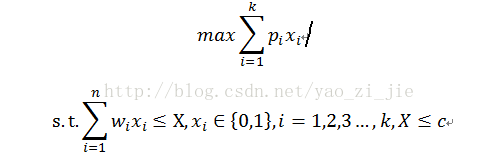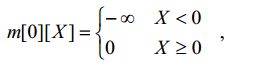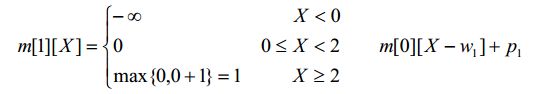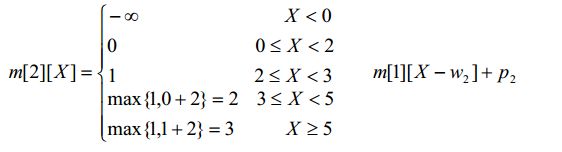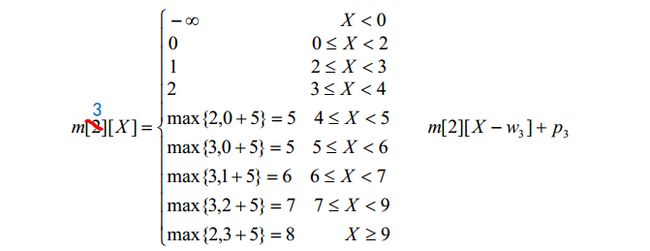动态规划算法的个人理解

多段图最短路径规划问题

我们知道，问题可以采用动态规划算法进行解决的一个重要性质即是该问题必须具备最优子结构性质，所谓的最优子结构性质用大白话说就是指原问题的最优解必然包含了原问题的子问题的一个最优解。这样听起来还是挺绕的，因此下面先通过一个实例，即多段图最短路径规划问题来理解下什么是最优子结构性质，以及采用动态规划算法解决问题的一些基本步骤。

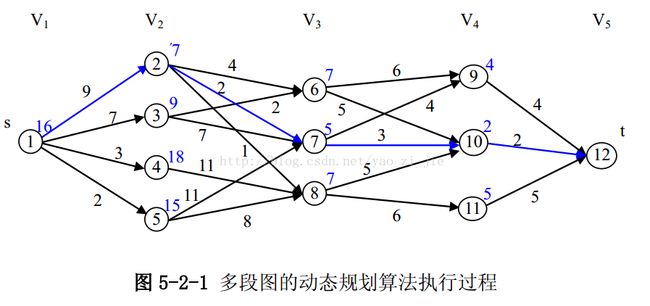
多段图最短路径问题是理解动态规划算法的一个较为容易的问题。该问题的一个实例图（有向图）如下。可看出该图中共有12个节点（小圆圈中带标记那些）；然后每条边上都附上了节点到节点间的连接权值，可以理解为从节点到节点间的路径长度；其中V1~V5表明该有向图被分成了5段，第一段仅含有源节点s，第五段仅含有终点t，而V2段含有4个节点分别为2、3、4、5，V3段含有3个节点分别为6、7、8，V4段含有3个节点分别为9、10、11。多段图最短路径规划问题的目的是找到一条从s-t的路径，且该路径的长度最短（即选择的路径的各边的权值加和最小）。

假如采用贪心算法解决上述问题，从源点出发，采取的贪心准则是每次都取当前两个子段图间连接的最短值，则选择的路径是s->4->8->10->t，总的路

径长度为3+11+5+2=21，显然这不是最短路径，因为像s-2-7-10-t这一条路径的总的路径长度为9+2+3+2=16。因此首先要明确动态规划算法与贪心算

法的区别，因为贪心算法并没有关心全局最优，每次只是选取当前的局部最优解。在多段图最短路径问题中，贪心算法在两个子段图的连接中选择了当

前两个子段图间最短的那一段，但是这样的选择可能会导致后面的路径选择错过了实际最优的选择。

采用动态规划算法解决多段图最短路径规划问题的思想就是，我们要计算每一个子段图到下一个子段图的所有可能的连接情况，并保留每种可能选择中

最短的那个连接，假设我们从终点反推到起点，则具体的操作可以是这样的：

1、首先计算V4段到t的各可能路径长度，即9、10、11到t的路径长度，明显为9->t的最短路径长度为4，10->t的最短路径长度为2，11->t的最短路径长

度为5，可以简记为(9,t)=4，(10,t)=2，(11,t)=5，下面也会一直采用这种简记方式。

2、继续计算V3段到t的各可能路径长度，此时对于节点6，有两种选择，分别为6->9->t和6->10->t，此时分别对应的路径长度为6+4=10和5+2=7（注意

此处的4和2分别是指(9,t)和(10,t)，即V4段中各节点到t的最短距离），此时保留最短的一段，简记为(6,t)=7。同理，7->t的路径选择有7->9->t和7->10-

>t，路径长度分别为4+4=8和3+2=5，保留最短的一段，简记为(7,t)=5。同理可计算出(8,t)=7。

依此类推，对于V2段，有：

(2,t)=min(4+(6,t) ,2+(7,t) ,1+(8,t))=min(4+7,2+5,1+7)=7，

(3,t)=min(2+(6,t) ,7+(7,t))=min(2+7,7+5)=9，

(4,t)=min(4+(8,t))=min(11+7)=18，

(5,t)=min(11+(7,t),8+(8,t))=min(11+5,8+7)=15。

最后有 (s,t)=min(s+(2,t),s+(3,t),s+(4,t),s+(5,t))=min(9+7,7+9,3+18,2+15)=16，

3、综上有此时可以选择两条路径，即s->2->7->10->t和s->3->6->10->12，最短路径为16，这是全局最优解。

从上面的推演过程中可以看出动态规划算法每一次都会保留所有可能的选择策略中的最优者，因为总体的最优必然包含某个局部最优解，而构成全局最

优的局部最优解不一定就是当前的可选的最优解，例如贪心算法每次都是选择最短的连接，但是其实在贪心策略下所得的解并不是全局最优。因此需要

将所有情况都做一个记录。

一般我们采用动态规划算法解决问题时，首先要明确问题是否具有最优子结构，然后找出问题最优子结构的递推关系式，例如多段图最短路径规划问题

中的递推公式可表述如下：

cost(i,j) = min{ c(j,l) + cost(i+1,l) }，l∈Vi+1，(j,l)∈E，E为多段图的边集，Vi+1为第i+1段中的点集

其中cost(i,j)表示的是第i段的第j个顶点到终点t的路径长度的最短值，l为第i+1段中的某个顶点，然后c(j,l)为顶点j到l之间的连接权值，即距离值。一般的

可采用动态规划进行求解的问题，只要能够找到对应的递推表达式，就可以很容易地编写出相应的代码（用递归方式编写代码会很直观，但是这样往往

会导致一个子问题被重复计算多次，因此常采用备忘录的方式，即保存每次迭代计算所得的子问题的解，然后后续在利用到子问题的解时仅需要做查表

的工作即可，因此大大降低了时间复杂度，当然这样要付出空间代价），例如多段图最短路径的代码。

0/1背包问题

动态规划算法中比较经典的一个问题是0/1背包问题，0/1背包问题即是有一堆物品和一个背包，物品有质量和价值两个属性，背包有容量限制，问如何

装这些物品使得背包所能获得的总价值最大，且所装物品的总质量不会超过背包的容量限制。通俗点说就是对于一个物品，我们选择要不要将它放入背

包中，0即表示不放入，1即表示放入，最终对所有物品是否放入背包会构成一个决策仅含0或1的决策序列，这个决策序列能够满足背包装物品的总重

量不会超过背包容量的限制。0/1背包问题对应了一个整数规划问题如下：

0/1背包问题具有最优子结构，其递推关系式可表示为：

其中m[k][c]表示当背包容量为c时，对第k个物品是否放入背包中进行决策后（是否放入）对应的背包的最优总价值。解释上述的递推关系式即是，当前

背包容量为c，现在要放入第k个物品，此时有两种可选策略，一种是不放入，一种是放入。不放入则此时的价值与对第k-1个物品是否放入的决策的价

值是一致的，且背包容量维持为c不变；而如果选择放入，则此时放入物品后的背包总容量要减掉第k个物品的重量，而总价值为对前面k-1个物品进行

决策后的价值加上第k个物品的价值所得的总价值。

可以通过一个实例的推演来理解这个问题：假设有3个物品，质量分别为(w1,w2,w3)=(2,3,4)，价值分别为(p1,p2,p3)=(1,2,5)，背包容量为6。按顺序

放入物品，下文中的X即是当前背包容量，此时对于m[0][X]，满足：

对于m[1][X]，满足：

对于m[2][X]，满足：其中当3≤X<5时，max{1,0+2}中的1是放入第一个物品后的价值，而0+2意味着此时选择放入第二个物品，则无论第一个物品无法

放入，因为已经超过了背包的容量范围。

对于m[3][X]，满足：

从上面的推演可以看出，每对一个新物品是否加入背包进行决策，都需要考虑前面的物品是否加入背包的决策的最优情况，最终背包问题的最优解综合

了所有物品是否加入背包的最优决策。而针对每一个物品是否放入的决策都保存在m[][]这个二维数组中，因此每次计算新问题的时候都不需要在对子问

题进行重复计算，只是直接调用m[][]中对应的数组项即可。通过0/1背包问题的递推表达式，可以较为容易地写出0/1背包问题的程序：0/1背包问题程

序。

参考博客：

http://blog.csdn.net/huahuahailang/article/details/9042935

http://blog.csdn.net/yeepom/article/details/8712224