KNN及影响其算法性能的优化(交叉验证、是否过拟合等)——自学第二篇
- 介绍实现KNN的两种基础算法
- 通过使用交叉验证、防止过拟合、超参数调整等方法对KNN的计算精度进行调整。
- 总结KNN算法和机器学习流程
-
- 1、KNN(K近邻)
-
-
- 方法一:底层算法
- 方法二:利用skleran库
-
-
- 2、影响KNN算法性能的优化
- 3、超参数
-
-
- (1)超参数——K
- (2)超参数——距离权重
- (3)超参数——P
-
-
- 4、网格搜索
- 5、KNN总结
- 6、机器学习的流程
- 1、KNN(K近邻)
1、KNN(K近邻)
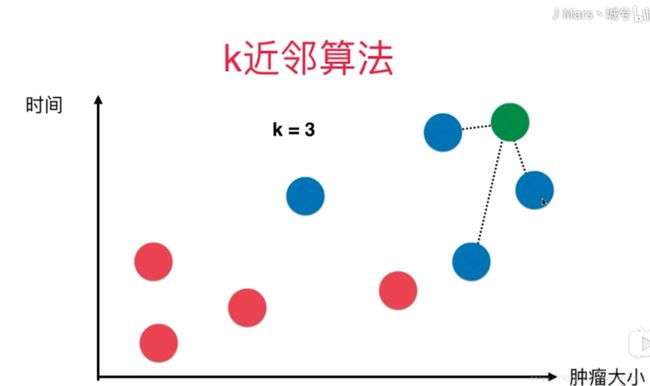
如图所示为每一个病人的肿瘤大小与其发现肿瘤的时间的关系,以此来判断肿瘤是否为恶性,其中恶性为蓝色,良性为红色,如果新来的病人为绿色的,需要用knn判断是否为恶性。
若k值取3,则找出之前数据中的点离新的数据点的距离最近的三个点,再分别将这三个点进行投票,若三个点中蓝色的居多,则新的点也为蓝色(恶性),反之则为红色(良性)。
上图所示离绿色点最近的三个点中,有两个为红色一个为蓝色,所以最终绿色的点属于红色(良性)。
新的数据属于离它最近的k个数据中数量最多的类别
距离通过计算两个点(a和b)的欧拉距离得到:
注:其中i为某一个点的第i个维度上的坐标
整体代码如下:
方法一:底层算法
from numpy import *
import operator
import matplotlib.pyplot as plt
##给出训练数据以及对应的类别
def createDataSet():
group = array([[1.0, 2.0], [1.2, 0.1], [0.1, 1.4], [0.3, 3.5]])
labels = ['A', 'A', 'B', 'B']
return group, labels
###通过KNN进行分类
def classify(input, dataSet, label, k):
dataSize = dataSet.shape[0]
####计算欧式距离
diff = tile(input, (dataSize, 1)) - dataSet # 将测试数据在行方向上重复datasize次,列方向上重复1次,即展开成训练数据格式
sqdiff = diff ** 2
squareDist = sum(sqdiff, axis=1) ###行向量分别相加,从而得到新的一个行向量
dist = squareDist ** 0.5
##对距离进行排序
sortedDistIndex = argsort(dist) ##argsort()根据元素的值从大到小对元素进行排序,返回下标
print(sortedDistIndex)
classCount = {}
for i in range(k):
voteLabel = label[sortedDistIndex[i]]
###对选取的K个样本所属的类别个数进行统计
classCount[voteLabel] = classCount.get(voteLabel, 0) + 1 #字典中的键voteLabel,若没有则添加键的默认值位0
###选取出现的类别次数最多的类别
maxCount = 0
for key, value in classCount.items(): #.item遍历字典中所有键
if value > maxCount:
maxCount = value
classes = key #返回出现次数最多的类别
return classes
if __name__ == '__main__':
dataSet, labels = createDataSet()
plt.scatter(dataSet[:,0],dataSet[:,1])
plt.show()
input = array([1.1, 0.3])
K = 1
output = classify(input, dataSet, labels, K)
print("测试数据为:", input, "分类结果为:", output)
# 1)计算测试数据与各个训练数据之间的距离;
#
# 2)按照距离的递增关系进行排序;
#
# 3)选取距离最小的K个点;
#
# 4)确定前K个点所在类别的出现频率;
#
# 5)返回前K个点中出现频率最高的类别作为测试数据的预测分类。方法二:利用skleran库
采用scikit-learn中已经封装好的knn库
from sklearn.neighbors import KNeighborsClassifier # K最近邻(kNN,k-NearestNeighbor)分类算法
#建立模型,创建实例
knn = KNeighborsClassifier(n_neighbors=3) #k=3
#训练模型
knn.fit(X_train, y_train)
#将准确率打印出
print(knn.score(X_test, y_test))
#预测某个数x
knn.predict(x)
#最好将x写成数组的形式
x_predict=x.reshape(1,-1)
knn.predict(x_predict)scikit-learn中训练模型的步骤
- 加载机器学习模块
- 创建算法实例(将算法的类实例化)并传入参数
- 拟合训练数据集,训练模型
- 用predict预测数据
2、影响KNN算法性能的优化
问题:如果用所有的数据集都输入模型得到的模型很差并且没有其他的数据对其进行调整,那遇到新的数据时的预测效果会不好。(用所有的数据都作为训练集是不恰当的)
解决:
- 分训练集和测试集:训练集和测试集为7:3,用训练数据训练模型,再用测试集检验模型好坏
from sklearn.datasets import load_iris # iris数据集
from sklearn.neighbors import KNeighborsClassifier # K最近邻(kNN,k-NearestNeighbor)分类算法
import matplotlib.pyplot as plt #可视化模块
#直接用k近邻算法
#加载iris数据集
iris = load_iris()
X = iris.data
y = iris.target
#分割数据并
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3) #将数据集中30%作为测试集
#建立模型
knn = KNeighborsClassifier()
#训练模型
knn.fit(X_train, y_train)
#将准确率打印出
print(knn.score(X_test, y_test))
- 交叉验证
from sklearn.datasets import load_iris # iris数据集
from sklearn.neighbors import KNeighborsClassifier # K最近邻(kNN,k-NearestNeighbor)分类算法
from sklearn.cross_validation import cross_val_score # K折交叉验证模块
import matplotlib.pyplot as plt #可视化模块
#直接用k近邻算法
#加载iris数据集
iris = load_iris()
X = iris.data
y = iris.target
#建立模型
knn = KNeighborsClassifier()
#使用K折交叉验证模块(把样本分成5份,每一份都为训练集,得到精确度再求平均值)
scores = cross_val_score(knn, X, y, cv=5, scoring='accuracy')
#将5次的预测准确率打印出
print(scores)
# [ 0.96666667 1. 0.93333333 0.96666667 1. ]
#将5次的预测准确平均率打印出
print(scores.mean())可视化不同k值的精度和误差,并判断是否过拟合
from sklearn.datasets import load_iris # iris数据集
from sklearn.model_selection import train_test_split # 分割数据模块
from sklearn.neighbors import KNeighborsClassifier # K最近邻(kNN,k-NearestNeighbor)分类算法
from sklearn.cross_validation import cross_val_score # K折交叉验证模块
import matplotlib.pyplot as plt #可视化模块
#************************************************************************************************
#加载iris数据集
iris = load_iris()
X = iris.data
y = iris.target
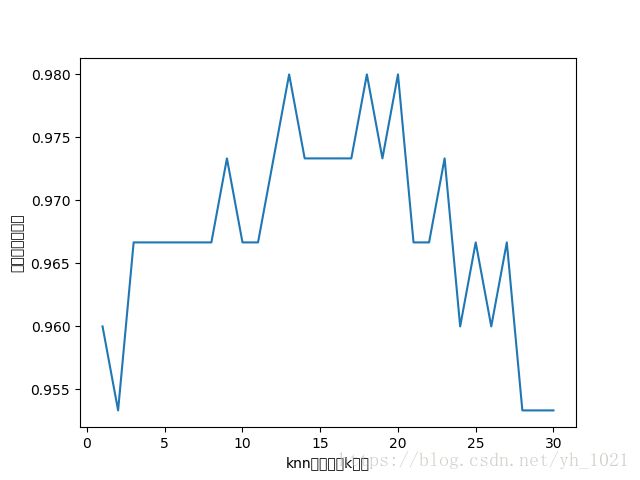
#通过对不同的k求精度值,得到精度最高的k值
k_range=range(1,31)
k_score=[]
max=0
index=0
for i in k_range:
knn = KNeighborsClassifier(n_neighbors=i)
score=cross_val_score(knn,X,y,cv=10,scoring='accuracy')
if score.mean() > max:
max = score.mean()
index = i
k_score.append(score.mean())
print('k is %d' %index)
plt.plot(k_range,k_score)
plt.xlabel('knn中近邻数k的值')
plt.ylabel('交叉验证精确度')
plt.show()
#************************************************************************************************
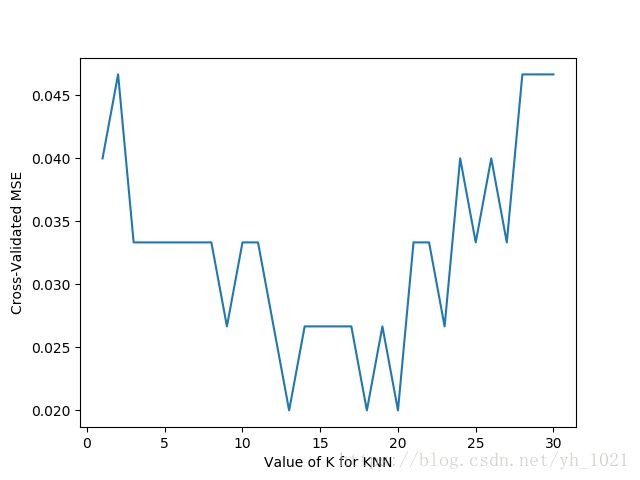
#用平均方差(Mean squared error)判断模型好坏
k_scores=[]
for k in k_range:
knn = KNeighborsClassifier(n_neighbors=k)
loss = -cross_val_score(knn, X, y, cv=10, scoring='mean_squared_error')
k_scores.append(loss.mean())
plt.plot(k_range, k_scores)
plt.xlabel('Value of K for KNN')
plt.ylabel('Cross-Validated MSE')
plt.show()
#************************************************************************************************
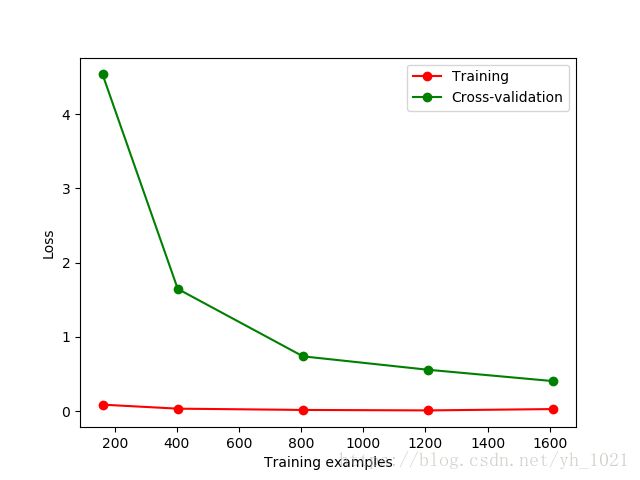
#通过学习曲线模块看是否产生过拟合
from sklearn.learning_curve import learning_curve #学习曲线模块
from sklearn.datasets import load_digits #digits数据集
from sklearn.svm import SVC #Support Vector Classifier
import matplotlib.pyplot as plt #可视化模块
import numpy as np
#通过学习曲线模块看是否产生过拟合
digits = load_digits()
X = digits.data
y = digits.target
#得到训练集的样本数,训练集上的分数和测试集上的分数,也可以选择优化器SVC,选择精确度计算方式(此为平均方差)
train_sizes, train_loss, test_loss = learning_curve(
SVC(gamma=0.0008), X, y, cv=10, scoring='mean_squared_error',
train_sizes=[0.1, 0.25, 0.5, 0.75, 1])
#平均每一轮所得到的平均方差(共5轮,分别为样本10%、25%、50%、75%、100%)
train_loss_mean = -np.mean(train_loss, axis=1)
test_loss_mean = -np.mean(test_loss, axis=1)
#可视化模型
plt.plot(train_sizes, train_loss_mean, 'o-', color="r",
label="Training")
plt.plot(train_sizes, test_loss_mean, 'o-', color="g",
label="Cross-validation")
plt.xlabel("Training examples")
plt.ylabel("Loss")
plt.legend(loc="best") #显示图例
plt.show()
#************************************************************************************************
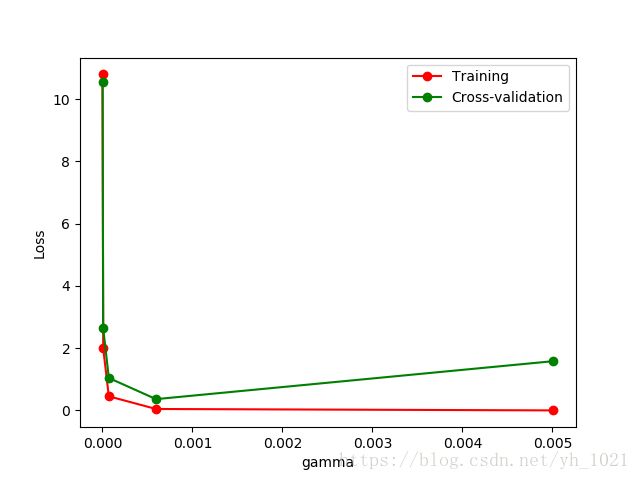
#用验证曲线 validation curve 选择超参数gamma,找到正常拟合的参数,防止过拟合和欠拟合
from sklearn.learning_curve import validation_curve #validation_curve模块
from sklearn.datasets import load_digits
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import numpy as np
#digits数据集
digits = load_digits()
X = digits.data
y = digits.target
#建立参数测试集
param_range = np.logspace(-6, -2.3, 5) #gamma取值为10e-6到10e-2.3中的5个数
#使用validation_curve快速找出参数gamma对模型的影响
train_loss, test_loss = validation_curve(
SVC(), X, y, param_name='gamma', param_range=param_range, cv=10, scoring='mean_squared_error')
#平均每一轮的平均方差
train_loss_mean = -np.mean(train_loss, axis=1)
test_loss_mean = -np.mean(test_loss, axis=1)
#可视化图形
plt.plot(param_range, train_loss_mean, 'o-', color="r",
label="Training")
plt.plot(param_range, test_loss_mean, 'o-', color="g",
label="Cross-validation")
plt.xlabel("gamma")
plt.ylabel("Loss")
plt.legend(loc="best")
plt.show()用平均方差来计算不同k值的误差曲线
通过学习曲线模块看是否产生过拟合
用验证曲线 validation curve 选择超参数gamma,找到正常拟合的参数,防止过拟合和欠拟合,如图可知选择gamma=0.001时未发生过拟合。
3、超参数
- 超参数:在算法运行前需要决定的参数
- 模型参数:算法过程中学习的参数
(1)超参数——K
上面已经讨论过不同的k值对模型的精确度的影响,可以通过遍历k值得到精确度的折线图
(2)超参数——距离权重
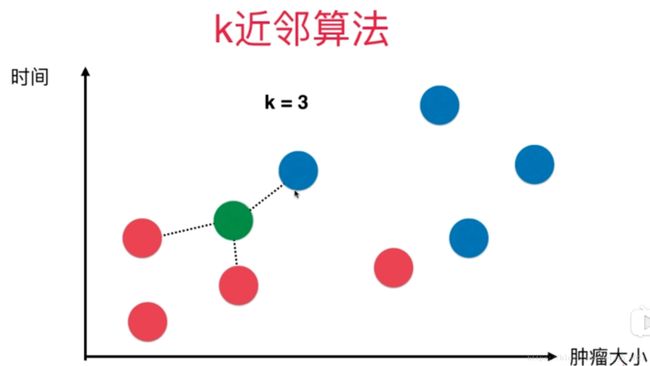
在KNN中K的值为超参数,当然除此以外还有很多超参数。比如下图所示的KNN算法中,若只考虑离绿色的点最近的三个点中哪一类的数量最多,那么绿色的点将属于蓝色。

但是很明显绿色的点离红色的更近,所以在使用KNN算法中还需要将距离的权重考虑在内。将距离的倒数作为权重,距离越远,权重越小。

考虑了距离权重之后能够很好的解决平票问题,若K=3时,距离绿色点最近的三个点分别为三个不同的分类,则需要根据权重的大小选择最优解。
from sklearn.neighbors import KNeighborsClassifier # K最近邻
knn=KNeighborsClassifier(n_neighbors=k, weights="uniform",)
#若weights=uniform则不计入权重,若weights=distance,sklearn则会考虑距离权重(3)超参数——P
明科夫斯基距离:
若P等于1,该式子为曼哈顿距离,当P=2为欧拉距离
(可设置不同的P值,得到精确度最高的P)
总结:可使用搜索的策略,遍历各项超参数,得到精确度最高的一组超参数
4、网格搜索
概念:Grid Search:一种调参手段,是一种穷举搜索:在所有候选的参数选择中,通过循环遍历,尝试每一种可能性,表现最好的参数就是最终的结果。其原理就像是在数组里找最大值。(为什么叫网格搜索?以有两个参数的模型为例,参数a有3种可能,参数b有4种可能,把所有可能性列出来,可以表示成一个3*4的表格,其中每个cell就是一个网格,循环过程就像是在每个网格里遍历、搜索,所以叫grid search)
作者:七八音
链接:https://www.jianshu.com/p/55b9f2ea283b
來源:简书
简书著作权归作者所有,任何形式的转载都请联系作者获得授权并注明出处。
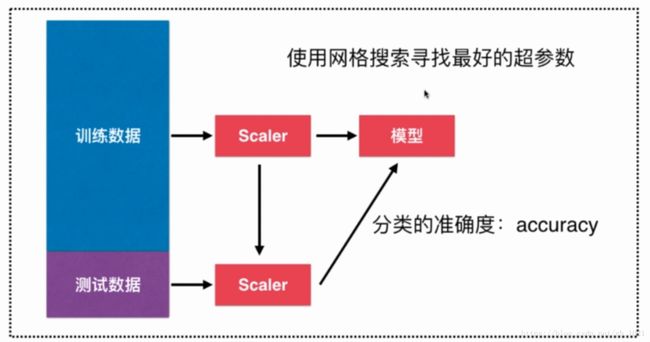
将网格搜索和交叉验证相结合能得到更好的模型,sklearn中有这样的类GridSearchCV将两者相结合,这个类实现了fit,predict,score等方法,被当做了一个estimator,使用fit方法可得到最佳参数
from sklearn.model_selection import GridSearchCV
#把要调整的参数以及其候选值列出来,写成字典形式;
param_grid = {"gamma":[0.001,0.01,0.1,1,10,100],
"C":[0.001,0.01,0.1,1,10,100]}
print("Parameters:{}".format(param_grid))
grid_search = GridSearchCV(SVC(),param_grid,cv=5) #实例化一个GridSearchCV类,第一个为模型,第二个为超参数值,第三个为交叉验证个数
X_train,X_test,y_train,y_test = train_test_split(iris.data,iris.target,random_state=10)
grid_search.fit(X_train,y_train) #训练,找到最优的参数,同时使用最优的参数实例化一个新的SVC estimator。
#grid_search.best_estimator 可以得到最佳分类器和里面的参数
#grid_search.best_score_ 可以得到最佳准确度
print("Test set score:{:.2f}".format(grid_search.score(X_test,y_test)))
print("Best parameters:{}".format(grid_search.best_params_)) #得到最佳参数
print("Best score on train set:{:.2f}".format(grid_search.best_score_))
作者:七八音
链接:https://www.jianshu.com/p/55b9f2ea283b
來源:简书
简书著作权归作者所有,任何形式的转载都请联系作者获得授权并注明出处。输出:
Parameters:{'gamma': [0.001, 0.01, 0.1, 1, 10, 100], 'C': [0.001, 0.01, 0.1, 1, 10, 100]}
Test set score:0.97
Best parameters:{'C': 10, 'gamma': 0.1}
Best score on train set:0.98
作者:七八音
链接:https://www.jianshu.com/p/55b9f2ea283b
來源:简书
简书著作权归作者所有,任何形式的转载都请联系作者获得授权并注明出处。
grid_search = GridSearchCV(SVC(),param_grid,cv=5,n_jobs=-1,verbose=2)
#n_jobs为并行处理时采用几个核计算,-1为根据电脑情况选择核的数量
#verbose为了在搜索的过程中有结果的输出,可以了解搜索的过程,数值越大输出的信息越详细。注:因为时穷举搜索,耗时比较长,先定大范围再细化
5、KNN总结
- 解决多分类问题
- 思想简单,功能强大
- 可以解决回归问题
离绿色点最近的有三个蓝色点,可以将距离作为权值,求出三个点的加权平均作为绿色点的值,也可直接将三个点的平均值作为绿色点的值,从而进行值的预测。
缺点:
- 效率低下,计算量大
- 与数据高度相关,若3个近邻中有两个误差大的数据,则会有很大影响
- 预测结果不具有可解释性,只能知道某个数据属于某一类,但无法知道为什么
- 如果数据维数较多,会发生维数灾难,随着维度增加,“看似相近”的两个点的
距离会越来越大(10000维的距离就为100)