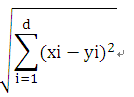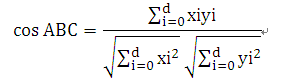聚类算法(一)层次聚类
聚类
聚类是对点集进行考察并按照某种距离测度将他们聚成多个“簇”的过程。聚类的目标是使得同一簇内的点之间的距离较短,而不同簇中点之间的距离较大。
一、聚类算法介绍
层次法聚类和点分配法聚类。
1.1 点、空间和距离
点集是一种适合于聚类的数据集,每个点都是某空间下的对象。一般意义上,空间只是点的全集,也就是说数据集中的点从该集合中抽样而成。特别地,欧式空间下的点就是实数向量。向量的长度就是空间的维度数,而向量的分量通常称为所表示点的坐标(coordinate)。
能够进行聚类的所有空间下都有一个距离测度,即给出空间下任意两点的距离。一般的欧氏距离(点的坐标在各个维度上差值的平方和的算术平方根)可以作为所有欧式空间下的距离测度。
现代聚类问题可能并不这么简单。他们可能牵涉非常高维的欧式空间或者根本不在欧式空间下聚类。比如,基于文档间高频区分词的共现情况来依据主题对文档聚类。而按照电影爱好者所喜欢的电影类别对他们进行聚类。
1.2 聚类策略
按照聚类算法使用的两种不同的基本策略,可以将聚类算法分成两类。
1) 层次(hierarchical)或凝聚式(agglomerative)算法。
这类算法一开始将每个点都看成簇。簇与簇之间按照接近度(closeness)来组合,接近度可以按照“接近”的不同含义采用不同的定义。当进一步的组合导致多个原因之下的非期望结果时,上述组合过程结束。比如停止条件为:达到预先给定的簇数目,或者使用簇的紧密度测度方法,一旦两个小簇组合之后得到簇内的点分散的区域较大就停止簇的构建。
2) 点分配过程算法。按照某个顺序依次考虑每个点,并将它分配到最适合的簇中。该过程通常有一个短暂的初始簇估计阶段。一些变形算法允许临时的簇合并或分裂的过程,或者当点为离群点时允许不将该点分配到任何簇中。
聚类算法也可以使用如下方式分类:
1) 欧式空间下,我们可以将点集合概括为其质心,即点的平均。而在非欧式空间下根本没有质心的概念,因此需要其他的簇概括方法。
2) 算法是否假设数据足够小的能够放入内存?或者说数据是否必须主要存放在二次存储器?由于不能将所有簇的所有点都同时放入内存,所以我们将簇的概括表示存放在内存中也是必要的。
1.3 维数灾难
“灾难”的一个体现是,在高维空间下,几乎所有点对之间的距离都差不多相等。另一个表现是,几乎任意的两个向量之间都近似正交。
1. 高维空间下的距离分布
一个d维欧式空间,假设在一个单位立方体内随机选择n个点,每个点可以表示成[x1,x2,…,xd],其每个xi都是0到1之间。假定d非常大,两个随机点[x1,x2,…,xd]和[y1,y2,…,yd]之间的欧式距离为
上述基于随机数据的论证结果表明,在这么多所有距离近似相等的点对之中发现聚类是很难的一件事。
2. 向量之间的夹角
在d维空间的随机点A,B,C,其中d很大。AC可以在任意位置,而B处于坐标原点。那么夹角ABC的余弦为:
当d不断增长时,分母会随d线性增长,但是分子却是随机值之和,可能为正也可能为负。分子期望为0,分子最大值为 。所以对于很大的d而言,任意两个向量的夹角余弦值几乎肯定接近为0,即夹角近似度等于90度。
推论为:如果dAB = d1, dBC=d2,dAC≈ 。
二、层次聚类
首先考虑欧式空间下的层次聚类。该算法仅可用于规模相对较小的数据集。层次聚类用于非欧式空间时,还有一些与层次聚类相关的额外问题需要考虑。因此,当不存在簇质心或者说簇平均点时,可以考虑采用簇中心点(clustroid)来表示一个簇。
2.1 欧式空间下的层次聚类
首先,每个点看作一个簇,通过不断的合并小簇而形成大簇。我们需要提前确定
(1) 簇如何表示?
(2) 如何选择哪两个簇进行合并?
(3) 簇合并何时结束?
对于欧式空间,(1)通过簇质心或者簇内平均点来表示簇。对于单点的簇,该点就是簇质心。可以初始化簇数目为欧式空间点的数目Cnumber=n。簇之间的距离为质心之间的欧式距离,
(2)选择具有最短距离(或者其他方式)的两个簇进行合并。
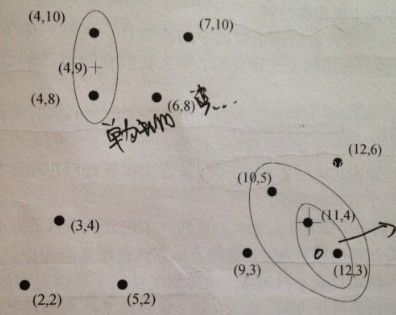
例如,有如下12个点,首先我们将每一个点看做一个簇。
point.txt文件
4 10
4 8
7 10
6 8
3 4
2 2
5 2
9 3
10 5
11 4
12 3
12 6
#include
#include
#include
#include
using namespace std;
const int iniClusNum = 12;
const int stopNum = 3;
class Point
{
public:
double x;
double y;
int NumPBelong;
Point()
{
x=0;
y=0;
NumPBelong = -1;
}
Point(double x1, double y1, int f=-1):x(x1),y(y1),NumPBelong(f){}
const Point& operator=(const Point& p)
{
x = p.x;
y=p.y;
NumPBelong = p.NumPBelong;
return *this;
}
};
class ManagerP
{
public:
double getDistance(const Point& p1, const Point& p2)
{
return sqrt(pow((p1.x-p2.x),2)+pow((p1.y-p2.y),2));
}
Point getMean(const Point& p1, const Point& p2)
{
Point p;
p.x = (p1.x+p2.x)/2;
p.y=(p1.y+p2.y)/2;
return p;
}
};
class ManagerC
{
public:
Point Cluster[iniClusNum];
vector ClusterLast[iniClusNum];
bool isIndexClose[iniClusNum];
bool isIndexClose2[iniClusNum];
void initCluster()//use txt to init, import txt
{
ifstream myfile ( "point.txt" ) ;
if ( !myfile )
{
cout << "cannot open file." ; return ;
}
Point p;
int x,y;
int i=0;
while(!myfile.eof())
{
myfile>>x>>y;
p.x=x;
p.y=y;
Cluster[i]=p;
i++;
}
myfile.close();
}
void initIndexClose()
{
for(int i=0;i::iterator ite=ClusterLast[i].begin();
for(;ite!= ClusterLast[i].end();ite++)
{
cout<<*ite<<"\t";
}
cout<stopNum)
{
double min=INT_MAX;
int x=-1,y=-1;
ManagerP mp;
for(int i=0;i::iterator ite = ClusterLast[Cluster[y].NumPBelong].begin();//put y's node in x
for(;ite!=ClusterLast[Cluster[y].NumPBelong].end();ite++)
{
ClusterLast[Cluster[x].NumPBelong].push_back(*ite);
}
ClusterLast[Cluster[y].NumPBelong].clear();
isIndexClose[y]=true;//y is closed
p.NumPBelong = Cluster[x].NumPBelong;
Cluster[x]=p;//new p is open
}
ClustNum--;
}
int total_size =0;
for(int i=0;i