图论算法——加权无向图的数据结构

引言

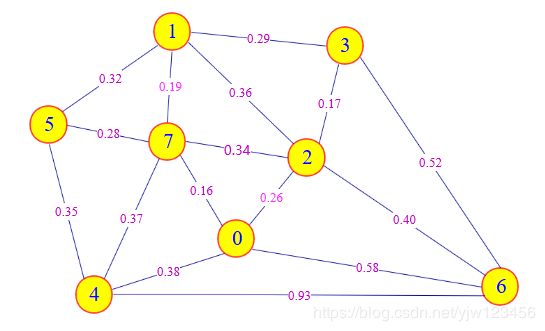
我们要在一幅加权连通无向图中找到它的最小生成树。首先要考虑的是如何表示这个无向图。

有关概念可参考博文数据结构之图的概述

加权边的表示

package com.algorithms.graph;

/**
 * 带权重的无向边的数据结构(不可变类)
 *
 * @author yjw
 * @date 2019/5/23/023
 */
public final class Edge implements Comparable<Edge> {
    /**
     * 边的两个顶点v,w
     */
    private final int v;
    private final int w;
    //边的权重
    private final double weight;


    public Edge(int v, int w, double weight) {
        this.v = v;
        this.w = w;
        this.weight = weight;
    }

    /**
     * 返回边的权重
     *
     * @return
     */
    public double weight() {
        return weight;
    }

    /**
     * 当两个顶点都不知道时可以调用该方法
     * (either:(两者中的) 任何一个)
     * @return 边的顶点之一
     */
    public int either() {
        return v;
    }

    /**
     * 返回边上的另一个顶点
     *
     * @param vertex
     * @return
     */
    public int other(int vertex) {
        if (vertex == v) {
            return w;
        } else if (vertex == w) {
            return v;
        }
        throw new RuntimeException("No that vertex");
    }

    @Override
    public int compareTo(Edge that) {
        if (this.weight < that.weight) {
            return -1;
        } else if (this.weight > that.weight) {
            return +1;
        }
        return 0;
    }

    @Override
    public String toString() {
        return String.format("%d-%d(%.2f)", v, w, weight);
    }
}

这是无向边的实现，因为是无向的，因此该边的两个顶点的邻接集中都可以引用它。这里设计为不可变的使我们不需要担心变化后会怎样。

关于不可变类的设计可阅读博文《Effective Java 3rd》读书笔记——类和接口之使类和成员的可访问性最小化

边定义好了之后我们再来定义加权无向图的结构

加权无向图的表示

package com.algorithms.graph;

import java.util.HashSet;
import java.util.Set;

/**
 * 加权无向图的数据结构
 * @author yjw
 * @date 2019/5/23/023
 */
@SuppressWarnings("unchecked")
public class EdgeWeightedGraph {
    private final int vertexNum;
    private int edgeNum;
    private Set<Edge>[] adj;

    public EdgeWeightedGraph(int vertexNum) {
        this.vertexNum = vertexNum;
        this.edgeNum = 0;
        adj = (Set<Edge>[]) new HashSet[vertexNum];
        for (int v = 0; v < vertexNum; v++) {
            adj[v] = new HashSet<>();
        }
    }

    public int vertexNum() {
        return vertexNum;
    }

    public int edgeNum() {
        return edgeNum;
    }

    /**
     * 增加一条边
     * TODO 注意 可能两个不同的Edge对象有相同的顶点信息，就是允许平行边的存在
     * @param e
     */
    public void addEdge(Edge e) {
        int v = e.either(),w = e.other(v);
        if (adj[v].add(e) && adj[w].add(e)) {
            edgeNum++;
        }
    }

    /**
     * 通过顶点的方式增加一条边(因为是无向图，所以起点和终点是哪个不重要)
     * @param start 边的起点
     * @param end  边的终点
     * @param weight 权重
     */
    public void addEdge(int start,int end,double weight) {
        addEdge(new Edge(start,end,weight));
    }

    //提供增加边的便利方法

    /**
     * 以同一起点增加两条边
     */
    public void addEdges(int start,int end1,double weight1,int end2,double weight2) {
        addEdge(start,end1,weight1);
        addEdge(start,end2,weight2);
    }

    /**
     * 增加三条边
     */
    public void addEdges(int start,int end1,double weight1,
                         int end2,double weight2,
                         int end3,double weight3) {
        addEdges(start,end1,weight1,end2,weight2);
        addEdge(start,end3,weight3);
    }


    /**
     * 增加四条边
     */
    public void addEdges(int start,int end1,double weight1,
                         int end2,double weight2,
                         int end3,double weight3,
                         int end4,double weight4) {
        addEdges(start,end1,weight1,end2,weight2,end3,weight3);
        addEdge(start,end4,weight4);
    }

    /**
     * 增加五条边
     */
    public void addEdges(int start,int end1,double weight1,
                         int end2,double weight2,
                         int end3,double weight3,
                         int end4,double weight4,
                         int end5,double weight5) {
        addEdges(start,end1,weight1,end2,weight2,end3,weight3,end4,weight4);
        addEdge(start,end5,weight5);
    }


    public Iterable<Edge> adj(int v) {
        return adj[v];
    }

    /**
     * 返回加权无向图中的所有边
     * @return
     */
    public Iterable<Edge> edges() {
        Set<Edge> set = new HashSet<>();
        for (int v = 0; v < vertexNum; v++) {
            set.addAll(adj[v]);//用了Set就不用担心重复问题
        }
        return set;
    }

    @Override
    public String toString() {
        StringBuilder s = new StringBuilder("(" + vertexNum + " vertices, " + edgeNum + " edges)\n");
        for (int v = 0; v < vertexNum; v++) {
            s.append(v).append(": ");
            for (Edge e: this.adj(v)) {
                s.append(e).append(" ");
            }
            s.append("\n");
        }
        return s.toString();
    }

    public static void main(String[] args) {
        //构造时注意不要重复添加
        EdgeWeightedGraph g = new EdgeWeightedGraph(8);
        g.addEdges(0,6,.58,2,.26,4,.38,7,.16);
        g.addEdges(1,3,.29,2,.36,7,.19,5,.32);
        g.addEdges(2,6,.40,7,.34,3,.17);
        g.addEdge(3,6,.52);
        g.addEdges(4,6,.93,7,.37,5,.35);
        g.addEdge(5,7,.28);

        System.out.println(g);
    }

}

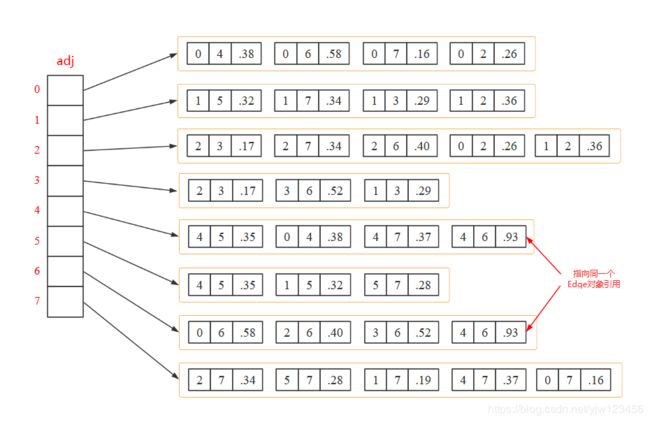
该实现只是在无向图的邻接表实现中用Edge对象代替了Graph中的整数来表示边上的两个顶点。添加了一些增加无向边的便利方法，虽然写起来有点麻烦，但是还是很好用的。

我们就来通过这个类构造上面这个图吧，构造代码：

EdgeWeightedGraph g = new EdgeWeightedGraph(8);
g.addEdges(0,6,.58,2,.26,4,.38,7,.16);
g.addEdges(1,3,.29,2,.36,7,.19,5,.32);
g.addEdges(2,6,.40,7,.34,3,.17);
g.addEdge(3,6,.52);
g.addEdges(4,6,.93,7,.37,5,.35);
g.addEdge(5,7,.28);

System.out.println(g);

输出：

(8 vertices, 16 edges)
0: 0-4(0.38) 0-6(0.58) 0-7(0.16) 0-2(0.26) 
1: 1-5(0.32) 1-7(0.19) 1-3(0.29) 1-2(0.36) 
2: 2-3(0.17) 2-7(0.34) 2-6(0.40) 0-2(0.26) 1-2(0.36) 
3: 2-3(0.17) 3-6(0.52) 1-3(0.29) 
4: 4-5(0.35) 0-4(0.38) 4-7(0.37) 4-6(0.93) 
5: 4-5(0.35) 1-5(0.32) 5-7(0.28) 
6: 0-6(0.58) 2-6(0.40) 3-6(0.52) 4-6(0.93) 
7: 2-7(0.34) 5-7(0.28) 1-7(0.19) 4-7(0.37) 0-7(0.16) 

对应的结构为：