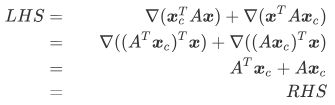机器学习线性回归最小二乘法推导及几何解释
文章目录
- 最小二乘法原理
- 代数解法
- 矩阵解法
- 几何解释
- 最小二乘法的局限性
最小二乘法原理
目 标 函 数 = ∑ ( 观 测 值 − 理 论 值 ) 2 目标函数 =\sum (观测值-理论值)^2 目标函数=∑(观测值−理论值)2
n个只有一个特征的训练样本为 ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x n , y n ) (x_1,y_1),(x_2,y_2),\cdots ,(x_n,y_n) (x1,y1),(x2,y2),⋯,(xn,yn)
拟合函数 f k , b ( x ) = k x + b f_{k,b}(x)=kx+b fk,b(x)=kx+b
则目标函数 J ( k , b ) = ∑ i = 1 n ( f ( x i ) − y i ) 2 = ∑ i = 1 n ( k x i + b − y i ) 2 J(k,b)=\sum_{i=1}^{n}(f(x_i)-y_i)^2=\sum_{i=1}^{n}(kx_i+b-y_i)^2 J(k,b)=∑i=1n(f(xi)−yi)2=∑i=1n(kxi+b−yi)2
代数解法
以k为未知数整理 J ( k , b ) J(k,b) J(k,b)得到:
J ( k ) = ∑ i = 1 n ( k x i + b − y i ) 2 = ( ∑ i = 1 n x i 2 ) k 2 + 2 ( ∑ i = 1 n x i ( b − y i ) ) k + ∑ i = 1 n ( b − y i ) 2 J(k) = \sum_{i=1}^{n}(kx_i+b-y_i)^2 = (\sum_{i=1}^{n}x_i^2)k^2+2(\sum_{i=1}^{n}x_i(b-y_i))k+\sum_{i=1}^{n}(b-y_i)^2 J(k)=i=1∑n(kxi+b−yi)2=(i=1∑nxi2)k2+2(i=1∑nxi(b−yi))k+i=1∑n(b−yi)2
以b为未知数整理 J ( k , b ) J(k,b) J(k,b)得到:
J ( b ) = ∑ i = 1 n ( k x i + b − y i ) 2 = n b 2 + ( 2 ∑ i = 1 n ( k x i − y i ) ) b + ∑ i = 1 n ( k x i − y i ) 2 J(b) = \sum_{i=1}^{n}(kx_i+b-y_i)^2 = nb^2+(2\sum_{i=1}^{n}(kx_i-y_i))b+\sum_{i=1}^{n}(kx_i-y_i)^2 J(b)=i=1∑n(kxi+b−yi)2=nb2+(2i=1∑n(kxi−yi))b+i=1∑n(kxi−yi)2
以上两式是关于 k k k或 b b b的开口向上的抛物线表达式,对于形如 y = a x 2 + b x + c y=ax^2+bx+c y=ax2+bx+c的抛物线其对称轴为 x = − b 2 a x=-\frac{b}{2a} x=−2ab,则当 x = − b 2 a x=-\frac{b}{2a} x=−2ab式,y取得极值(也是最值)。
所以有
b = − 2 ∑ i = 1 n ( k x i − y i ) 2 n = 1 n ( ∑ i = 1 n y i − k ∑ i = 1 n x i ) b=-\frac{2\sum_{i=1}^{n}(kx_i-y_i)}{2n}=\frac{1}{n}(\sum_{i=1}^{n}y_i-k\sum_{i=1}^{n}x_i) b=−2n2∑i=1n(kxi−yi)=n1(i=1∑nyi−ki=1∑nxi)
k = − 2 ( ∑ i = 1 n x i ( b − y i ) ) 2 ∑ i = 1 n x i 2 = ∑ i = 1 n ( x i y i ) − b ∑ i = 1 n x i ∑ i = 1 n x i 2 k=-\frac{2(\sum_{i=1}^{n}x_i(b-y_i))}{2\sum_{i=1}^{n}x_i^2}=\frac{\sum_{i=1}^{n}(x_iy_i)-b\sum_{i=1}^{n}x_i}{\sum_{i=1}^{n}x_i^2} k=−2∑i=1nxi22(∑i=1nxi(b−yi))=∑i=1nxi2∑i=1n(xiyi)−b∑i=1nxi
联立两式,求得 k , b k,b k,b
k = n ∑ i = 1 n x i y i − ( ∑ i = 1 n x i ) ( ∑ i = 1 n y i ) n ∑ i = 1 n x i 2 − ( ∑ i = 1 n x i ) 2 k=\frac{n\sum_{i=1}^{n}x_iy_i-(\sum_{i=1}^{n}x_i)(\sum_{i=1}^{n}y_i)}{n\sum_{i=1}^{n}x_i^2-(\sum_{i=1}^{n}x_i)^2} k=n∑i=1nxi2−(∑i=1nxi)2n∑i=1nxiyi−(∑i=1nxi)(∑i=1nyi)
b = ∑ i = 1 n x i 2 ∑ i = 1 n y i − ∑ i = 1 n x i ∑ i = 1 n x i y i n ∑ i = 1 n x i 2 − ( ∑ i = 1 n x i ) 2 b=\frac{\sum_{i=1}^{n}x_i^2\sum_{i=1}^{n}y_i-\sum_{i=1}^{n}x_i\sum_{i=1}^{n}x_iy_i}{n\sum_{i=1}^{n}x_i^2-(\sum_{i=1}^{n}x_i)^2} b=n∑i=1nxi2−(∑i=1nxi)2∑i=1nxi2∑i=1nyi−∑i=1nxi∑i=1nxiyi
矩阵解法
OLS的目标函数(矩阵形式)为: J ( w ) = ∥ y − X w ∥ 2 2 J(\mathbf{w})=\left \| \mathbf{y}-\textbf{X}\mathbf{w} \right \|_2^2 J(w)=∥y−Xw∥22
其中 X ∈ R m ∗ n , w ∈ R n ∗ 1 , y ∈ R m ∗ 1 \textbf{X}\in \mathbb{R}^{m*n},\mathbf{w}\in \mathbb{R}^{n*1},\mathbf{y}\in \mathbb{R}^{m*1} X∈Rm∗n,w∈Rn∗1,y∈Rm∗1
补充:实值函数对向量求导
- ∇ ( a T x ) = ∇ ( x T a ) = a \nabla(\boldsymbol{a}^T\boldsymbol{x}) = \nabla(\boldsymbol{x}^T\boldsymbol{a}) = \boldsymbol{a} ∇(aTx)=∇(xTa)=a
- 证明: ∂ a T x ∂ x i = ∂ ∑ j a j x j ∂ x i = ∂ a i x i ∂ x i = a i \dfrac{\partial\boldsymbol{a^Tx}}{\partial x_i} = \dfrac{\partial\sum_j a_j x_j}{\partial x_i} = \dfrac{\partial a_i x_i}{\partial x_i} = a_i ∂xi∂aTx=∂xi∂∑jajxj=∂xi∂aixi=ai
- ∇ ∣ ∣ x ∣ ∣ 2 2 = ∇ ( x T x ) = 2 x \nabla ||\boldsymbol{x}||_2^2 = \nabla(\boldsymbol{x}^T\boldsymbol{x}) = 2\boldsymbol{x} ∇∣∣x∣∣22=∇(xTx)=2x
- 证明: ∂ ∣ ∣ x ∣ ∣ 2 2 ∂ x i = ∂ ∑ j x j 2 ∂ x i = ∂ x i 2 ∂ x i = 2 x i \dfrac{\partial ||\boldsymbol{x}||_2^2}{\partial x_i} = \dfrac{\partial\sum_j x_j^2}{\partial x_i} = \dfrac{\partial x_i^2}{\partial x_i} = 2x_i ∂xi∂∣∣x∣∣22=∂xi∂∑jxj2=∂xi∂xi2=2xi
- ∇ ( x T A x ) = ( A + A T ) x \nabla (\boldsymbol{x}^TA\boldsymbol{x}) = (A+A^T)\boldsymbol{x} ∇(xTAx)=(A+AT)x
下面推导OLS的目标函数(矩阵形式):
J ( w ) = ∥ y − X w ∥ 2 2 = ( y − X w ) T ( y − X w ) = y T y − y T X w − w T X T y + w T X T X w J(\mathbf{w})=\left \| \mathbf{y}-\textbf{X}\mathbf{w} \right \|_2^2 =(\mathbf{y}-\textbf{X}\mathbf{w})^T(\mathbf{y}-\textbf{X}\mathbf{w}) =\mathbf{y}^T\mathbf{y}-\mathbf{y}^T\textbf{X}\mathbf{w}-\mathbf{w}^T\textbf{X}^T\mathbf{y}+\mathbf{w}^T\textbf{X}^T\textbf{X}\mathbf{w} J(w)=∥y−Xw∥22=(y−Xw)T(y−Xw)=yTy−yTXw−wTXTy+wTXTXw
上述式子中展开项的每一项实际都是标量,因为 X ∈ R m ∗ n , w ∈ R n ∗ 1 , y ∈ R m ∗ 1 \textbf{X}\in \mathbb{R}^{m*n},\mathbf{w}\in \mathbb{R}^{n*1},\mathbf{y}\in \mathbb{R}^{m*1} X∈Rm∗n,w∈Rn∗1,y∈Rm∗1,所以 y T y ∈ R 1 ∗ 1 \mathbf{y}^T\mathbf{y}\in \mathbb{R}^{1*1} yTy∈R1∗1,其余展开项同理可得也是标量。
对于标量 a a a我们知道 a T = a a^T=a aT=a,中间两项 y T X w , w T X T y \mathbf{y}^T\textbf{X}\mathbf{w},\mathbf{w}^T\textbf{X}^T\mathbf{y} yTXw,wTXTy互为转置,又都是标量,所以实际二者相等。
又因为 ∇ x ( x T A x ) = ( A + A T ) x \nabla_\boldsymbol{x} (\boldsymbol{x}^TA\boldsymbol{x}) = (A+A^T)\boldsymbol{x} ∇x(xTAx)=(A+AT)x,所以 w T X T X w = ( X T X + ( X T X ) T ) w = 2 X T X w \mathbf{w}^T\textbf{X}^T\textbf{X}\mathbf{w}=(\textbf{X}^T\textbf{X}+(\textbf{X}^T\textbf{X})^T)\mathbf{w}=2\textbf{X}^T\textbf{X}\mathbf{w} wTXTXw=(XTX+(XTX)T)w=2XTXw
y T y \mathbf{y}^T\mathbf{y} yTy与 w \mathbf{w} w无关,所以 ∇ w ( y T y ) = 0 \nabla_\mathbf{w} (\mathbf{y}^T\mathbf{y}) = 0 ∇w(yTy)=0
则 J ( w ) J(\mathbf{w}) J(w)对 w \mathbf{w} w求导,得: ∂ J ( w ) ∂ w = − 2 X T y + 2 X T X w \frac{\partial J(\mathbf{w})}{\partial \mathbf{w}}=-2\textbf{X}^T\mathbf{y}+2\textbf{X}^T\textbf{X}\mathbf{w} ∂w∂J(w)=−2XTy+2XTXw
令 ∂ J ( w ) ∂ w = 0 ⇒ − 2 X T y + 2 X T X w = 0 ⇒ X T X w = X T y \frac{\partial J(\mathbf{w})}{\partial \mathbf{w}}=0\Rightarrow -2\textbf{X}^T\mathbf{y}+2\textbf{X}^T\textbf{X}\mathbf{w}=0\Rightarrow \textbf{X}^T\textbf{X}\mathbf{w}=\textbf{X}^T\mathbf{y} ∂w∂J(w)=0⇒−2XTy+2XTXw=0⇒XTXw=XTy
w ^ O L S = ( X T X ) − 1 X T y \widehat{\mathbf{w}}_{OLS}=(\textbf{X}^T\textbf{X})^{-1}\textbf{X}^T\mathbf{y} w OLS=(XTX)−1XTy
几何解释

如上图n个特征向量 ( x 1 , x 2 , ⋯ , x n ) (x_1,x_2,\cdots ,x_n) (x1,x2,⋯,xn)组成一个n维空间。不失一般性,假设n=2。
X w \textbf{X}\mathbf{w} Xw是 ( x 1 , x 2 , ⋯ , x n ) (x_1,x_2,\cdots ,x_n) (x1,x2,⋯,xn)的线性组合, y − X w \mathbf{y}-\textbf{X}\mathbf{w} y−Xw是图中的红色向量,
目标函数为 J ( w ) = ∥ y − X w ∥ 2 2 J(\mathbf{w})=\left \| \mathbf{y}-\textbf{X}\mathbf{w} \right \|_2^2 J(w)=∥y−Xw∥22,几何意义即为使 y − X w \mathbf{y}-\textbf{X}\mathbf{w} y−Xw的模长最小,三角形中斜边大于直角边,所以当且仅当 X w \textbf{X}\mathbf{w} Xw是 y \mathbf{y} y在平面上的投影,即 y − X w \mathbf{y}-\textbf{X}\mathbf{w} y−Xw与平面垂直时目标函数有最小值
对于两个列向量 a , b \textbf{a},\textbf{b} a,b,若 a ⊥ b \textbf{a}\perp \textbf{b} a⊥b,则 a T b = 0 \textbf{a}^{T}\textbf{b}=0 aTb=0,
所以有 X T ( y − X w ) = 0 \textbf{X}^T(\mathbf{y}-\textbf{X}\mathbf{w})=0 XT(y−Xw)=0(向量垂直平面)
X T ( y − X w ) = 0 ⇒ w ^ O L S = ( X T X ) − 1 X T y \textbf{X}^T(\mathbf{y}-\textbf{X}\mathbf{w})=0\Rightarrow \widehat{\mathbf{w}}_{OLS}=(\textbf{X}^T\textbf{X})^{-1}\textbf{X}^T\mathbf{y} XT(y−Xw)=0⇒w OLS=(XTX)−1XTy
最小二乘法的局限性
- 若 X T X \textbf{X}^T\textbf{X} XTX的逆矩阵不存在,则无法使用最小二乘法,此时可用梯度下降法求解
- 当特征n非常大时,计算 X T X \textbf{X}^T\textbf{X} XTX的逆矩阵很耗时
- 若拟合函数不是线性的,则无法使用最小二乘法