GCMC - Graph Convolutional Matrix Completion 图卷积矩阵补全 KDD 2018

论文：Graph Convolutional Matrix Completion （GCMC） 图卷积矩阵补全

作者：来自于荷兰阿姆斯特丹大学的Rianne van den Berg, Thomas N. Kipf（GCN的作者）, Max Welling

来源：KDD 2018 Workshop

论文链接：https://www.kdd.org/kdd2018/files/deep-learning-day/DLDay18_paper_32.pdf

Github链接：https://github.com/riannevdberg/gc-mc

图卷积神经网络（GCN）是现在深度学习的热点之一，这篇文章基于user-item的二部图（Bipartite graph），提出了一种图自编码器框架，从链路预测的角度解决推荐系统中的评分预测问题。此外，为了验证所提出的消息传递方案，在标准的协同过滤任务上测试了所提出的模型，并展示出了一个有竞争力的结果。

1 相关介绍

1.1 背景

随着电子商务和社交媒体平台的爆炸式增长，推荐算法已经成为许多企业不可或缺的工具。
其中，推荐系统的一个子任务就是矩阵补全。文中把矩阵补全视作在图上的链路预测问题：users和items的交互数据可以通过一个在user和item节点之间的二分图来表示，其中观测到的评分/购买用links来表示。因此，预测评分就相当于预测在这个user-item二分图中的links。

据此，作者提出了一个图卷积矩阵补全（GCMC）框架：在用深度学习处理图结构的数据的研究进展的基础上，对矩阵进行补全的一种图自编码器框架。这个自编码器通过在二部交互图中信息传递的形式生成user和item之间的隐含特征。这种user和item之间的隐含表示用于通过一个双线性的解码器重建评分links。

当推荐图中带有结构化的外部信息(如社交网络)时，将矩阵补全作为二部图上的链接预测任务的好处就变得尤为明显。将这些外部信息与交互数据相结合可以缓解与冷启动问题相关的性能瓶颈。实验证明了作者提出的的图自编码器模型能够有效地将交互数据与side information结合起来。进一步证明了，在纯协同过滤场景中，这种方法能够与最新最先进的方法竞争。

1.2 side information

边信息（Side Information）：是指利用已有的信息Y辅助对信息X进行编码，可以使得信息X的编码长度更短。

边信息一个通俗的例子是：假设到马场去赌马，根据每个马的赔率可以得到一个最佳的投资方案。但是如果知道赌马的一些历史数据，例如上几场的胜负情况，那么可以得出一个更优的投资方案。赌马中的历史数据就是边信息。

1.3 contributions

• 将图神经网络应用于带有结构化side information的矩阵补全任务，并证明这种简单消息传递模型比基于复杂图形的方法有更好的性能
• 我们引入了节点dropout，这是一种有效的正则化技术，它以固定的概率删除单个节点的所有传出消息的整个集合

1.4 相关介绍

自编码器

下面的基于user或item的自动编码器是一类最新最先进的协同过滤模型，可以看作是文中的图数据自编码器模型的一个特例，其中编码器只考虑user或item的embedding。

• Autorec: Autoencoders meet collaborative filtering，WWW 2015
• Dropout: a simple way to prevent neural networks from overfitting，2014
• [CF-NADE] A neural autoregressive approach to collaborative filtering，ICML 2016

Autorec是这的第一个这样的模型，在这个模型中，其中，部分观察到的user或item的评分向量通过编码器层投影到潜在空间，并使用均方重建误差损失的解码器层重建。

CF-NADE算法可视为上述自动编码器体系结构的一个特例。在基于user的场景中，消息只从items传递给users
，在基于item的情况下，反之亦然。和文中的自编码器不同的是，评级的items在编码器中被分配了默认的3级，从而创建了一个完全连接的交互图。CF-NADE在节点上强制执行随机排序，并通过随机剪切将传入的消息分成两组，只保留其中一组。因此，该模型可以看作是一个去噪自动编码器，在每次迭代中，输入空间的一部分被随机丢弃。

矩阵分解模型

文中提出的模型和很多矩阵分解方法有关：

• 概率矩阵分解(Probabilistic matrix factorization，2008) (PMF)：采样概率的方法，将矩阵$M$分解为$M\approx U{V}^T$
• BiasedMF( Matrix Factorization Techniques for Recommender Systems，2009):通过合并一个user和item的特定bias以及全局bias来改进PMF
• 神经网络矩阵分解 （Neural network matrix factorization，2015） (NNMF)：扩展了MF方法，通过前馈神经网络传递潜在的users和items特征
• 局部低秩矩阵近似（ Local low rank matrix approximation，ICML 2013）：利用低秩近似的不同(与entry相关)组合来重建评价矩阵entries

Matrix completion with side information

• 在matrix completion (MC)（Exact matrix completion via convex optimization，2012）中，目标是用一个低秩评分矩阵去近似一个评分矩阵。然而，秩最小化是一个棘手的问题，论文中将秩最小化替换为核范数最小化(矩阵奇异值的总和)，将目标函数转化为可处理的凸函数。
• Inductive matrix completion (IMC)（Provable inductive matrix completion，2013）将users和items的内容信息合并到特征向量中，将评分矩阵中观察到的元素近似为$M_{ij}=x_i^{T}U{V}^T{y}_j$，其中$x_i$和$y_j$分别代表user$i$和item$j$的特征向量。
• geometric matrix completion (GMC) model（Matrix completion on graphs，2014）通过以user图和item图的形式添加side information，引入了MC模型的正则化
• Collaborative Filtering with Graph Information: Consistency and Scalable Methods（INPS 2015） 针对图正则化矩阵补全问题，提出了一种更有效的交替最小二乘优化方法(GRALS)。
• RGCNN（Geometric matrix completion with recurrent multi-graph neural networks，NIPS 2017） 是和本文最相关的工作。探讨了基于切比雪夫多项式的users和items k-nearest图的谱图滤波器的应用。文中的模型在一个编码器-解码器步骤中直接建模评级图，而不是使用递归估计，速度有显著的提升。
• PinSage，这是一个高度可扩展的图卷积网络，基于GraphSAGE框架，用于推荐的web级图，其中对邻居进行下采样以增强可扩展性。与PinSage相比，此文关注包含于图的side information，例如以社交网络图的形式，并进一步引入正则化技术来提高泛化。

2 在二部图中矩阵补全作为一种连接预测

2.1 符号定义

• $M$:评分矩阵，维度为$N_u\times N_v$，其中$N_u$是users的数量，$N_v$是items的数量
• 非零的$M_{ij}$表示user$i$对item$j$的评分，$M_{ij}=0$表示一个没有观测到评分

图1表示了整个模型的流程。在一个二分的user-item交互图中，矩阵补全任务(即对未观察到的交互的预测)可以转换为链接预测问题，并使用端到端可训练的图自编码器进行建模。

• 交互数据可以用无向图G表示：$G=(\mathcal{W},\mathcal{E},\mathcal{R})$
• $\mathcal{W}={\mathcal{W}}_u\cup {\mathcal{W}}_v$；${\mathcal{W}}_u$表示user节点的集合,维度为$N_u$；${\mathcal{W}}_v$表示item节点的集合,维度为$N_v$
• 边 $\left(u_i,r,v_j\right)\in \mathcal{E}$带有含评分等级类型的标签，$r\in \{1,\dots ,R\}=\mathcal{R}$

2.2 Revisiting graph auto-encoders 图自编码器

先前的推荐系统的基于图的方法通常采用多级pipline（此论文有介绍：Recommendation as link prediction in bipartite graphs: A graph kernel-based machine learning approach），其中包括图特征提取模型和链接预测模型，所有这些都分别进行训练。 然而，通过使用端到端学习技术对图结构数据进行建模，通常可以显着改善结果，特别是使用图自动编码器用于在无向图上进行无监督学习和链接预测。

本文采用（Thomas N. Kipf and Max Welling. Variational graph auto-encoders. NIPS Bayesian Deep Learning Work- shop, 2016.）中介绍的setup，因为它可以有效利用（卷积）权重共享，并允许以节点特征的形式包含边信息。其中

图自编码器模型：$Z=f(X,A)$

• 输入：一个$N\times D$的特征矩阵$X$和一个图邻接矩阵$A$,$D$表示节点特征的数量
• 输出：一个$N\times H$的节点embedding矩阵$Z={\left[z_1,\dots ,z_N\right]}^T$,$H$表示embedding的size

解码器：$\check{A}=g(Z)$

• 输入：节点的embedding对$(z_i,z_j)$
• 输出：预测邻接矩阵中的各个tntries：${\check{A}}_{ij}$

对于推荐系统的二部图$G=(\mathcal{W},\mathcal{E},\mathcal{R})$，将编码器重新公式化:

• $\left[Z_u,Z_v\right]=f\left(X_u,X_v,M_1,\dots ,M_R\right)$，其中$M_r\in \{0,1{\}}^{N_u\times N_v}$表示评分等级类型$r\in \mathcal{R}$相关的邻接矩阵（此时为元素是1或0的矩阵，元素为1表示观测到评分等级类型，元素为0就表示没有观测到评分的）
• $Z_u$是user的embedding矩阵，维度为$N_u\times H$
• $Z_v$是item的embedding矩阵，维度为$N_v\times H$
• 单个user$i$的embedding是一个真值特征向量$z_i^u$
• 单个item$j$的embedding是一个真值特征向量$z_j^v$

类似地，对解码器重新公式化：

• $\check{M}=g\left(Z_u,Z_v\right)$，表示作用在user和item的embedding上的函数，返回一个重构的评分矩阵$\check{M}$，维度为$N_u\times N_v$

可以使用最小化$\check{M}$中的预测等级和$M$中观测到的ground-true等级的reconstruction error训练这个图自编码器。reconstruction error可以使用

• 均方根误差
• 当把评分等级分作不同类时，可以使用交叉熵损失

2.3 Graph convolutional encoder 图卷积编码器

本文针对推荐任务提出一种图自编码器的变体图卷积编码器。本文提出的编码器模型可以有效利用图形中各个位置之间的权重分配，并为每种边类型（或评分）$r\in \mathcal{R}$分配单独的处理通道。这种权值共享的形式受到了最近的一类卷积神经网络的启发，这些神经网络直接对图形结构的数据进行操作。图数据卷积层执行的局部操作只考虑节点的直接邻居，因此在图数据的所有位置都应用相同的转换。

局部图卷积可以看作是消息传递，其中特征值的信息被沿着图的边传递和转换

• Discriminative Embeddings of Latent Variable Models for Structured Data，ICML 2016
• Neural Message Passing for Quantum Chemistry 量子化学的神经信息传递，ICML 2017

文中为每个等级分配特定的转换，从item $j$到user $i$传递的信息${\mu }_{j\to i,r}$表示为

$${\mu }_{j\to i,r}=\frac{1}{c_{ij}}{W}_r{x}_j^v\text{\hspace{1em}(1)}$$

• $c_{ij}$表示正则化常数，选择$\left|\mathcal{N}\left(u_i\right)\right|$(left normalization)或$\sqrt{\left|\mathcal{N}\left(u_i\right)\right|\left|\mathcal{N}\left(v_j\right)\right|}$(symmetric normalization)
• $\mathcal{N}\left(u_i\right)$定义为user$i$的邻居集合
• $W_r$是一个边类型的参数矩阵
• $x_j^v$是item节点$j$的特征向量

从users到items的消息${\mu }_{i\to j,r}$也以类似的方式传递。在消息传递之后，对每个节点都进行消息累计操作：对每种评分$r$下的所有邻居 $\mathcal{N}\left(u_i\right)$求和，并将它们累积为单个矢量表示：

$$h_i^u=\sigma \left[\mathrm{accum}\left(\sum _{j\in {\mathcal{N}}_i\left(u_i\right)}{\mu }_{j\to i,1},\dots ,\sum _{j\in {\mathcal{N}}_R\left(u_i\right)}{\mu }_{j\to i,R}\right)\right]\text{\hspace{1em}(2)}$$

• accum（·）表示一个聚合运算，例如stack（·），或sum（·）
• $\sigma (\cdot )$表示激活函数，例如ReLU(·) = max(0, ·)

把中间的输出$h_i$进行转换就得到了每个user最终的embedding：

$$z_i^u=\sigma \left(W{h}_i^u\right)\text{\hspace{1em}(3)}$$
item的embedding$z_i^v$使用同样的参数矩阵$W$进行同样计算。在存在特定于user和item的辅助信息（side information）的情况下，文中将单独的参数矩阵用于users和items的embedding。

公式（2）称为一个图卷积层，公式（3）称为一个稠密层。可以通过使用适当的激活函数堆叠几层（任意组合）来构建更深层次的模型。在最初的实验中，发现堆叠多个卷积层并不能提高性能，而将卷积层与稠密层进行简单组合的效果最佳（一个卷积层后跟着一个稠密层）。

2.4 Bilinear decoder 双线性解码器

为了在二部交互图中重建links，考虑一个双线性解码器，把每个评分等级看作是一类。$\check{M}$表示user$i$和item$j$之间重建的评分等级。解码器通过对可能的评分等级进行双线性运算，然后应用softmax函数生成一个概率分布：

$$p\left({\check{M}}_{ij}=r\right)=\frac{e^{{\left(z_i^u\right)}^T{Q}_r{z}_j^v}}{{\sum }_{s=1}^R{e}^{{\left(z_i^u\right)}^T{Q}_s{v}_j}}\text{\hspace{1em}(4)}$$

• $Q_r$是一个维度为$H\times H$的可训练参数矩阵，$H$是user或item隐含特征的维度

预测的评分等级计算方式为

$${\check{M}}_{ij}=g\left(u_i,v_j\right)={\mathbb{E}}_{p\left({\check{M}}_{ij}=r\right)}[r]=\sum _{r\in R}rp\left({\check{M}}_{ij}=r\right)\text{\hspace{1em}(5)}$$

2.5 模型训练

Loss function

交叉熵损失

$$\mathcal{L}=-\sum _{i,j;{\Omega }_{ij}=1}\sum _{r=1}^{R}I\left[M_{ij}=r\right]\log p\left({\check{M}}_{ij}=r\right)\text{\hspace{1em}(6)}$$

• $I[k=l]=1$指示函数表示当$k=l$时值为1，否则为0
• $\Omega \in \{0,1{\}}^{N_u\times N_v}$作为未观察到的评分等级的mask，这样对于在$M$中的元素，如果值为1就代表观测到了的评分等级，为0则对应未观测到的。因此，只需要优化观测到的评分等级。

Mini-batching

• 只采样固定数量的user和item对。这既是一种有效的正则化方法，也减少了训练模型所需的内存，而训练模型是将整个movielens-10M放入GPU内存中所必需的
• 通过实验验证了当调整正则化参数时，mini-batches和full batches训练，在MovieLens-1M数据集可以得到相似的结果
• 对于除了MovieLens-10M之外的所有数据集，选择full batches训练，因为mini-batches训练收敛更快

Node dropout

• 为了使该模型能够很好地泛化到未观测到的评分等级，在训练中使用了dropout ，以一定概率$p_{dropout}$随机删除特定节点的所有传出消息，将其称为节点dropout。
• 在初始实验中，发现节点dropout比消息dropout更能有效地进行正则化
• 节点dropout也会使embedding更不受特定user或item的影响
• 在公式（3）的隐含层中使用了常规的dropout

Weight sharing

• 并不是所有的users和items对于同一个评分等级都有相同的评分，这可能导致在卷积层中的权重矩阵$W_r$的某些列优化得没有其他列频繁
• 在不同$r$的矩阵$M_r$间使用一些形式的权值共享对于消除上述优化过程中的问题是可取的

$$W_r=\sum _{s=1}^r{T}_s\text{\hspace{1em}(7)}$$

作为成对的双线性解码器正则化的一种有效方法，采用一组基权重矩阵$P_s$的线性组合形式的权值共享:

$$Q_r=\sum _{s=1}^{n_b}{a}_{rs}{P}_s\text{\hspace{1em}(8)}$$

• $s\in \left(1,\dots ,n_b\right)$
• $n_b$表示基权重矩阵$P_s$的数量
• $a_{rs}$是可学习的系数，这个系数决定了每一个解码器权重矩阵$Q_r$的线性组合
• 为了避免过拟合并减少参数的数量，基权重矩阵的数量$n_b$应低于评分级别的数量

2.6 Input feature representation and side information

包含每个节点信息的特征可以直接在输入时，以输入特征矩阵$X_u$和$X_v$的形式输入到图编码器中。然而，当特征矩阵中没有足够的信息来区分不同的users（或items）及其兴趣时，这就产生了信息流的瓶颈问题。为此，文中加入了user和item的side information：通过单独处理的通道直接在稠密隐含层中加入user节点$i$的side information$x_i^{u,f}$和item节点$j$的side information$x_j^{v,f}$。

对于user的特征向量:
$$z_i^u=\sigma \left(W{h}_i^u+W_2^{u,f}{f}_i^u\right)\text{ with }{f}_i^u=\sigma \left(W_1^{u,f}{x}_i^{u,f}+b^u\right)\text{\hspace{1em}(9)}$$

• $W_1^{u,f}$和$W_2^{u,f}$都是可训练的权重矩阵
• $b^u$是一个bias

类似地，对于item的特征向量：
$$z_i^v=\sigma \left(W{h}_i^v+W_2^{v,f}{f}_i^v\right)\text{ with }{f}_i^v=\sigma \left(W_1^{v,f}{x}_i^{v,f}+b^v\right)\text{\hspace{1em}(10)}$$

在图卷积层的节点输入特征矩阵$X_u$和$X_v$，选择包含图中每个节点的唯一的 one-hot 向量。

3 实验

数据集

• 来自论文（Geometric matrix completion with recurrent multi-graph neural networks，NIPS 2017）Flixster, Douban，YahooMusic预处理的子集
• MovieLens(100K, 1M, and 10M)

这些数据集包括users对items的评分并且以特征的形式合并了一些user/item的其他信息。

experiments settings

• accumulation function ( stack vs. sum )
• whether to use ordinal weight sharing in the encoder
• left vs. symmetric normalization
• dropout rate $p\in \{0.3,0.4,0.5,0.6,0.7,0.8\}$
• Adam optimizer，learning rate of 0 . 01
• weight sharing in the decoder with 2 basis weight matrices
• dense layer (no activation function)
• graph convolution (with ReLU )
• layer sizes of 500 and 75
• decay factor set to 0.995

3.1 MovieLens 100K

• 使用user 和 item side information，GCMC都要比其他方法更好

• 结果表明，在二部交互图上进行信息传递的简单的自编码模型比更复杂的递归估计有更好的性能

• RMSE:均方根误差

$$RMSE=\sqrt{MSE}=\sqrt{SSE/n}=\sqrt{\frac{1}{n}\sum _{i=1}^n{w}_i{\left(y_i-{\hat{y}}_i\right)}^2}$$

• side information:users(e.g. age, gender, and occupation)，movies(genres)

3.2 MovieLens 1M and 10M

3.3 Flixster, Douban and YahooMusic

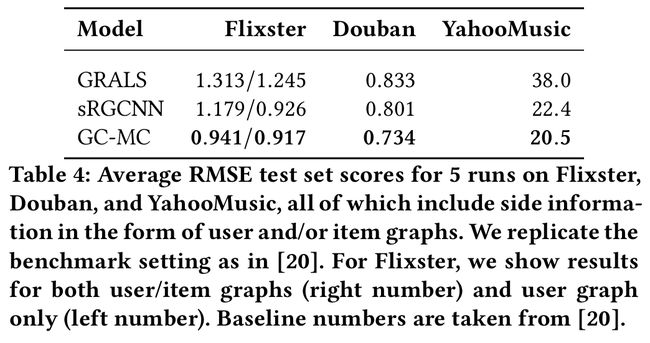
• 这些数据集以图的形式包含users和items的side information
• 通过使用邻接向量(按度归一化)作为相应 user/item的特征向量，将这个基于图的side information集成到框架中

3.4 Cold-start analysis

• 为了深入了解GC-MC模型对 side information的使用，还研究了模型中user的评分数据很少 (cold-start users)时的的性能。
• 采用了ML-100K基准数据集，因此对于固定数量的cold-start users $N_c$，除了最小数量$N_r$之外的所有评分都将从训练集中删除(实验中使用固定种子随机选择)。
• ML-100K在其原始形式中包含至少20个评分的user

• $N_r\in \{1,5,10\}$表示user的评分数量
• $N_c\in \{0,50,100,150\}$表示cold-start user的数量
• 虚线表示没有side information的实验
• 实线表示有side information的实验
• 标准误差低于0.001，因此未显示

3.5 讨论

在二部交互图上进行信息传递的简单的自编码模型比更复杂的递归估计有更好的性能。性能提高的原因：

• 消息传递在图中的差异。在sRGCNN中，分别使用user和item的k邻近图进行消息传递。因此，消息只在users之间和items之间传递。相反，GC-MC使用观察到的评分图来传递消息。结果，消息从在users发送到items，再从items发送到在users。在side information设置中，还使用Monti等人提供的k邻近来计算side information特征。
• 对应的图Laplacian的近似不同。sRGCNN使用Chebyshev展开(用user和item的k邻图近)，给定的p阶展开，就是考虑到从邻居节点到p-hop邻居的消息。GC-MC对于每个评分类型的二部相互图使用一阶近似，这样只访问每个节点的直接邻居。结果表明，一阶近似方法可以提高性能。

在ML-1M和ML-10M上的结果表明，有可能将文中方法扩展到更大的数据集，使其在预测性能方面接近最新最先进的基于user或item的协同过滤方法。

4 总结

• 提出了图卷积矩阵补全(GC-MC)模型:一种在推荐系统中用于矩阵补全任务的图自编码器框架。编码器包含一个图卷积层，它通过在二部user-item交互图上传递消息来构造users和items的embedding。结合双线性解码器，以标记边的形式预测新的评分。
• 图动编码器框架可以很自然地包含user和item的 side information。在有side information的情况下，文中提出的GC-MC模型比最近的相关方法表现得更好，这在一些基准数据集上得到了证明。在没有side information的情况下，GC-MC模型也取得了与目前最先进的协同过滤方法有竞争的结果。
• 文中提出的GC-MC模型可以扩展到大规模的多模态数据上(包括文本、图像和其他基于图的信息)。在这种情况下，GC-MC模型可以与循环或卷积神经网络相结合。