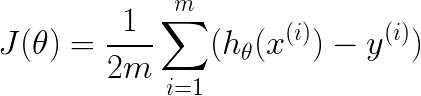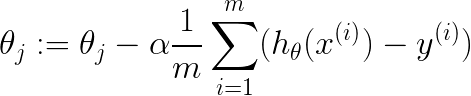0. 序
本文是对Stanford University的Machine Learning课程中Programming Exercise 1解题思路的记录
1. 文件说明
作业machine-learning-ex1文件夹中包含代码源文件夹ex1和作业说明文档ex1.pdf。
ex1.pdf主要内容包括以下几个部分:
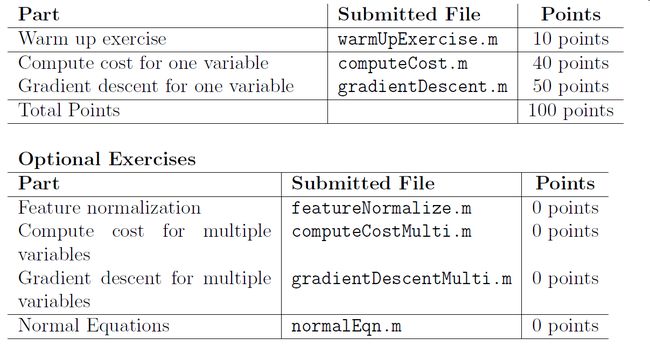
- 1. 需要完成的作业内容,其中标有星号的表示需要完成的,其他标记为可选作业
- 2. 作业得分情况:每个作业的得分不一样。
如果你完成了warm up exercise,你就能得到10分。在submit作业时,可以看到每一项的得分。
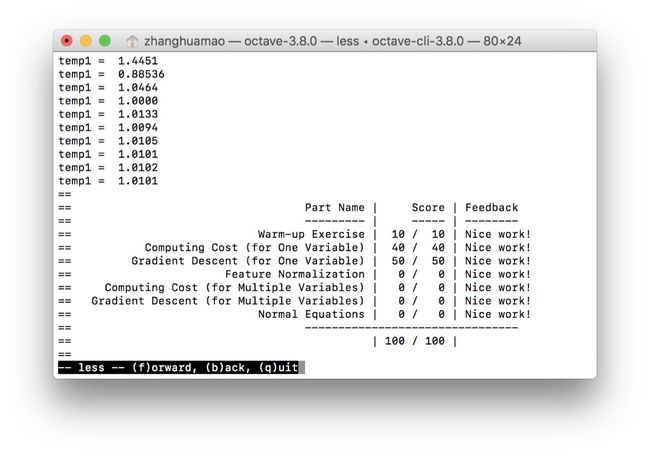
可选作业的总分为0,只能通过submit后的界面看到完成结果,Feedback为Nice work表示已完成。
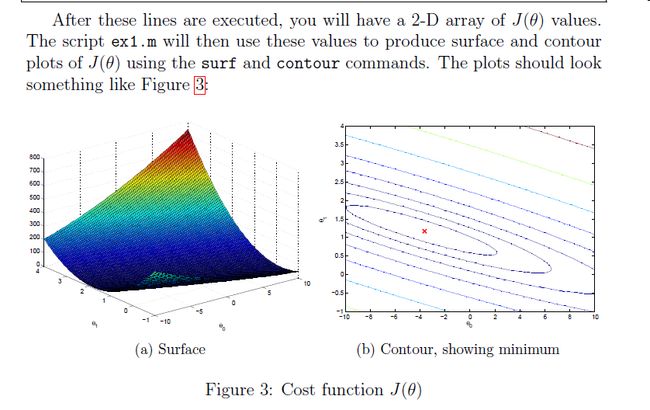
- 3. 每个需要完成的作业需要实现哪些内容?正确的运行结果长什么样子?
例如,当你完成了computeCost的代码,运行ex1.m,就可以得到这样两张图。
2. Warm up exercise
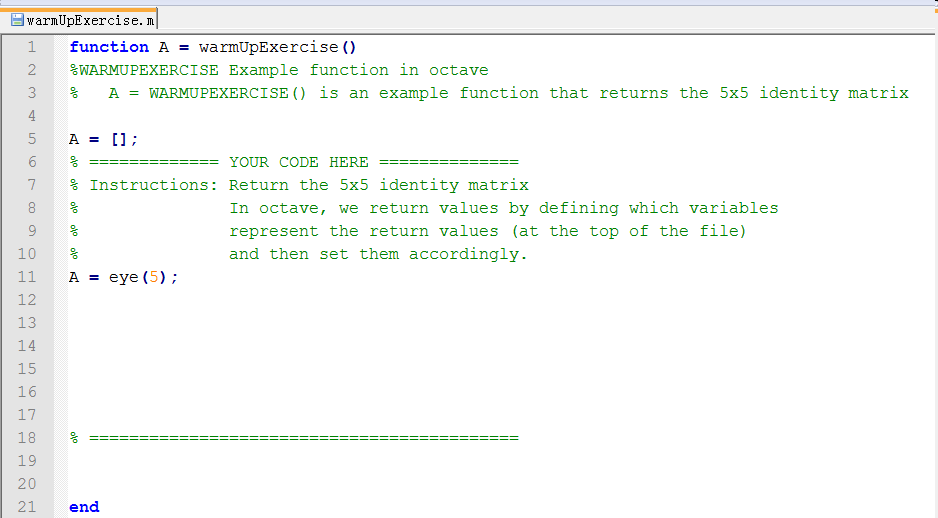
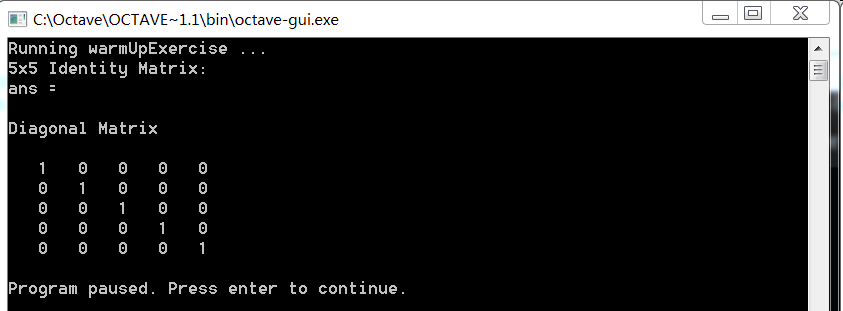
第一题是热身练习,比较简单,完成warmUpExercise.m中的代码,生成一个5x5的单位矩阵,ex1.pdf中对要实现的功能和运行结果都有说明,代码添加完成以后,在octave输入ex1就可以运行程序了。
下面是我添加的代码和运行结果
3. Plotting the Data
ex1data1.txt中存放的是ex1需要使用的training set,由于只有一个特征,第一列为特征值x,第二列为实际输出值y
通过plot函数,我们可以将这些值绘制出来,文档中已经告诉我们实现代码:
octave:65> data = load('ex1data1.txt');
octave:66> x = data(:, 1); y = data(:, 2);
octave:68> plot(x, y, 'rx', 'MarkerSize', 10);
octave:68> ylabel('Profit in $10,000s');
octave:69> xlabel('Population of City in 10,000s');
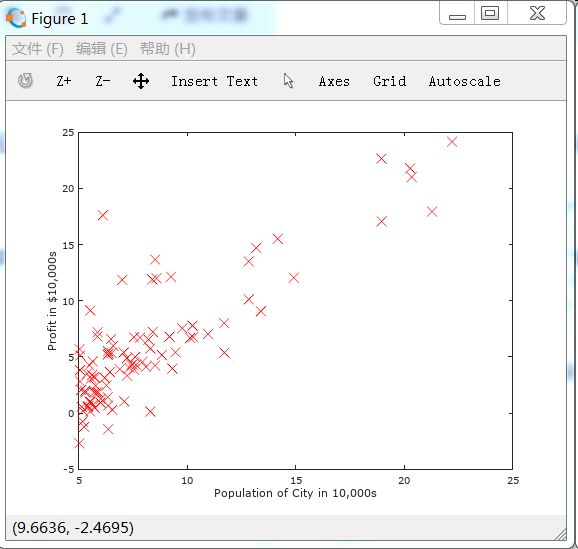
调用完这几句代码后,绘制结果如下图:
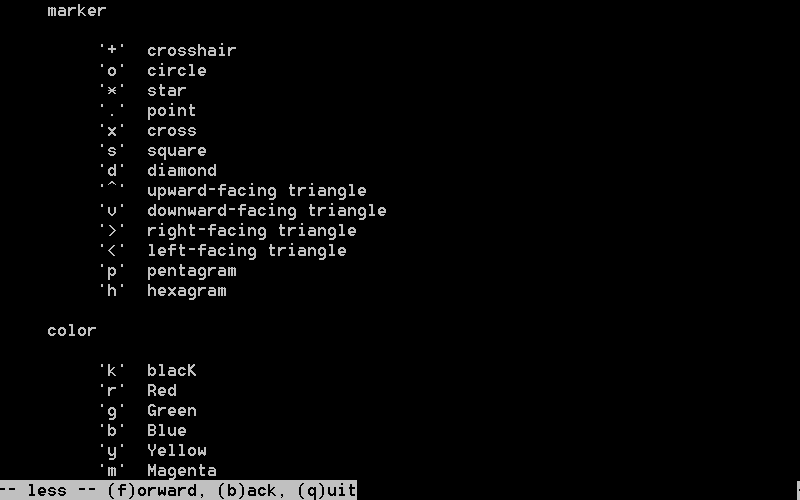
通过执行help plot命令,我们可以知道plot传入参数的含义,以plot(x, y, 'rx', 'MarkerSize', 10); 为例,其中的rx表示红色的X,MarkerSize和10决定了X显示的大小
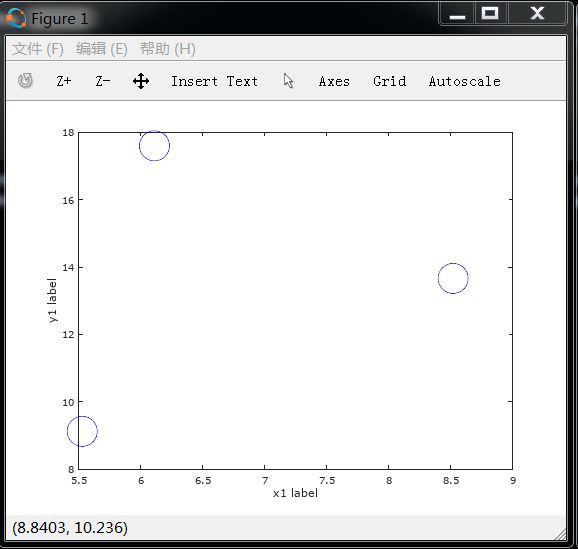
参考Plotting the Data的实现代码,我们可以自己实现一个简单的例子,使用plot函数绘制3个点(6.1101, 17.5920),(5.5277, 9.1302),(8.5186, 13.6620),这3个点显示为蓝色的圆圈。
octave:60> x1
x1 =
6.1101
5.5277
8.5186
octave:61> y1
y1 =
17.5920
9.1302
13.6620
octave:62> plot(x1, y1, 'bo', 'MarkerSize', 30);
octave:63> ylabel('y1 label');
octave:64> xlabel('x1 label');
ex1.m调用plotData的代码如下图所示:
4. Computing the cost
接着就是实现cost function的计算,cost function的公式如下图:
其中的假设函数可以通过向量化的方式来求和
我们可以先使用一组简单的数据来推算出假设函数的计算公式,假设我们现在有3个样本: (0.5, 2)、(0.3, 1.6)、(0.7, 1.8),theta0为1,theta2为2,代入cost function计算公式后,得到结果为0.06
对特征值X做向量化处理,给向量X增加了第一列值全为1,变成了3*2的矩阵。然后再初始化y和theta的值,通过以下步骤计算得出cost function为0.06
>X = [1 0.5;1 0.3; 1 0.7];
>y = [2; 1.6; 1.8];
>X
X =
1.00000 0.50000
1.00000 0.30000
1.00000 0.70000
>y
y =
2.0000
1.6000
1.8000
>theta = [1;2]
theta =
1
2
>X*theta
ans =
2.0000
1.6000
2.4000
>X*theta - y
ans =
0.00000
0.00000
0.60000
>(X*theta - y).^2 % 求得平方差
ans =
0.00000
0.00000
0.36000
>sum((X*theta - y).^2) % 求得平方差的和
ans = 0.36000
>size(X,1) % 计算样本个数m的值
ans = 3
>1/(2*length(y)) % 计算1/2m
ans = 0.16667
>(1/(2*length(y)))*(sum((X*theta - y).^2))
ans = 0.060000
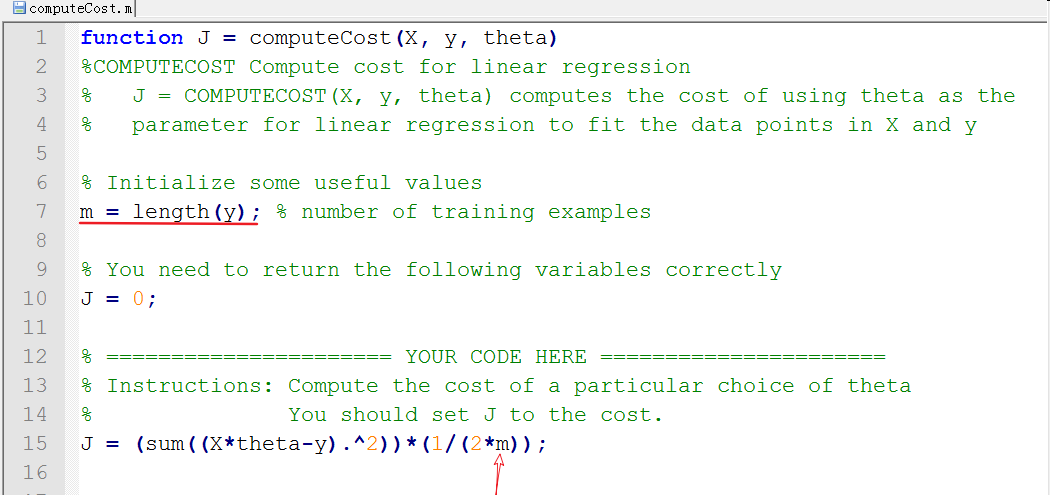
根据上述结果,得出Cost function的实现代码,补充代码到computeCost.m中
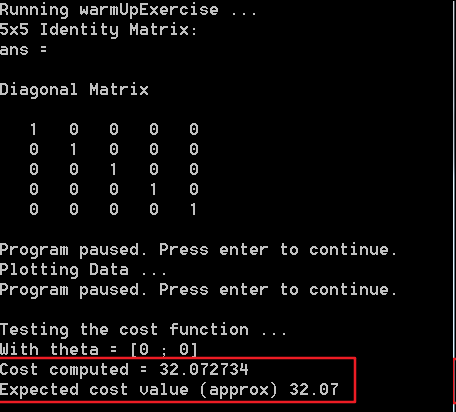
执行ex1.m,得到cost function的计算结果,Expected cost value表示正确结果,Cost computed表示通过computeCost.m计算的结果,两者一致,说明计算正确。
5. 梯度下降
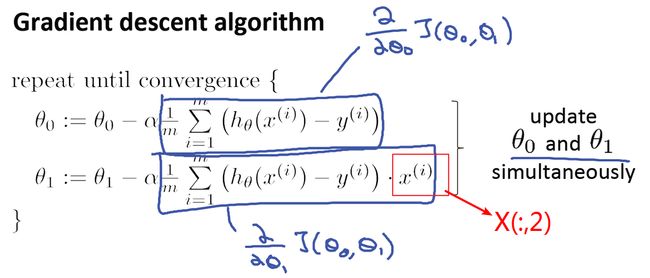
ex1.m中最后一个需要实现的是梯度下降算法,梯度下降的公式如下:
需要注意的一点是:需要同时更新theta0和theta1的值
我们也可以定义两个临时变量来保存theta0和theta1的值,括号里面求和的代码和cost function的类似,只是算出的值还需要乘以X(:,2)的求值,X(:,2)对应的就是第二列的特征值
>X
X =
1.00000 0.50000
1.00000 0.30000
1.00000 0.70000
>X(:,2)
ans =
0.50000
0.30000
0.70000
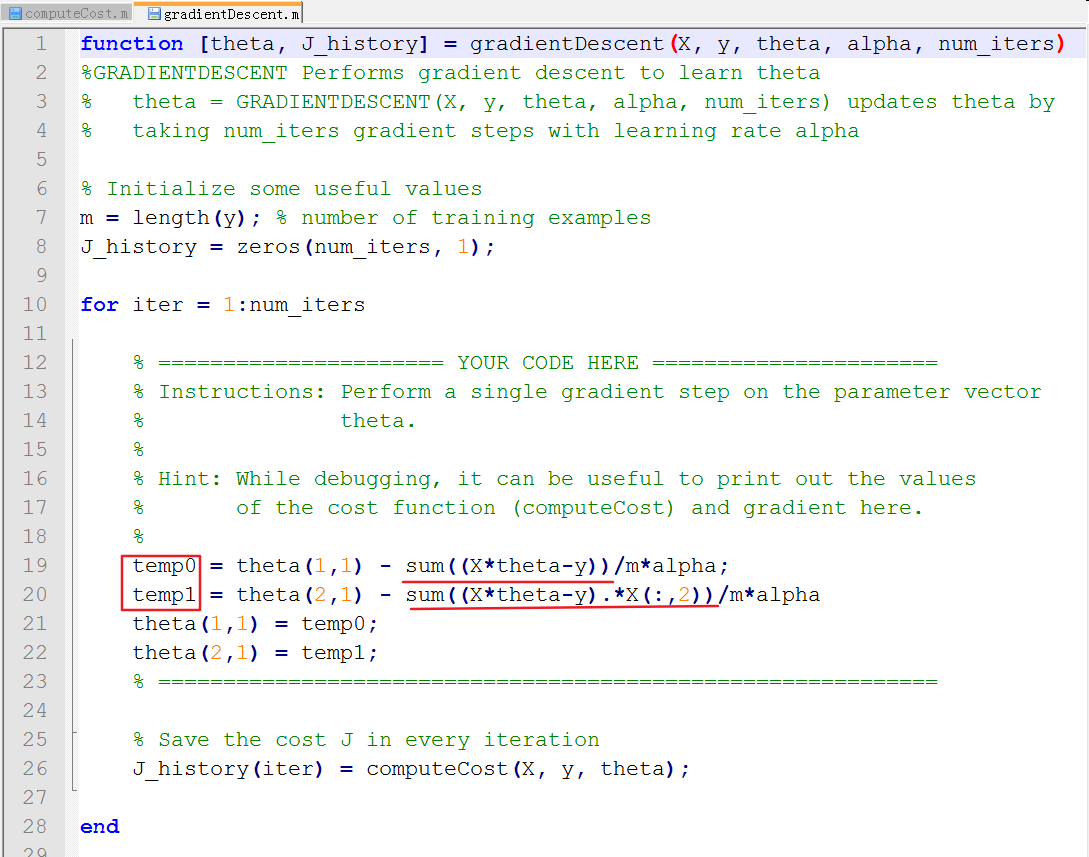
由于只有一个特征值,因此,带入theta0和theta1后,展开的公式如下图:
最终的实现代码如下图:
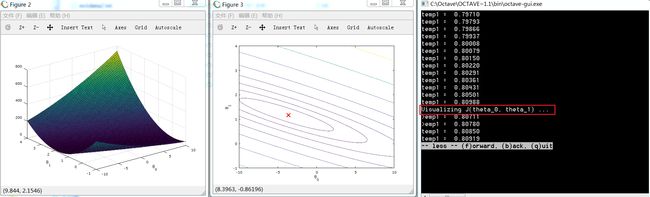
再次执行ex1,得到了运行结果:
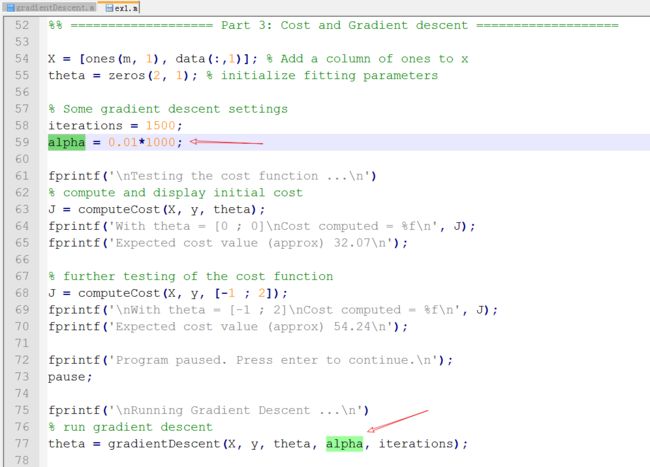
我们执行梯度下降时的learning rate是在ex1.m中设置的,我们可以尝试增大learning rate的值,来观察梯度下降是否收敛
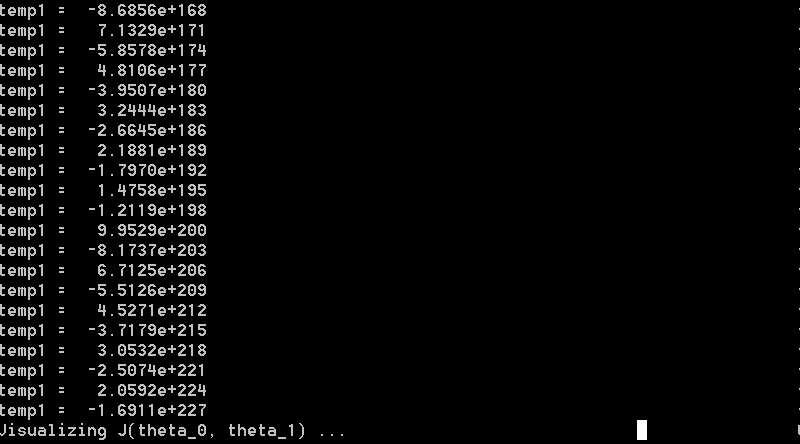
增大alpha值后,重新执行ex1,可以从打印的temp1值看到,theta值并没有逐步下降,而是来回变化