【文献阅读】BLOCK——用于VQA的双线性超对角融合模型（Hedi Ben-younes等人，AAAI，2019，有代码）

一、背景

文章题目：《BLOCK: Bilinear Superdiagonal Fusion for Visual Question Answering and Visual Relationship Detection》

AAAI2019的一篇文章。作者同时也是MUTAN的提出者，BLOCK也可以认为是MUTAN的改进版。MUTAN的项目地址可以参考：https://github.com/Cadene/vqa.pytorch#requirements

文章下载地址：https://aaai.org/ojs/index.php/AAAI/article/download/4818/4691

文章引用格式：Hedi Ben-younes, Remi Cadene, Nicolas Thome, Matthieu Cord. "BLOCK: Bilinear Superdiagonal Fusion for Visual Question Answering and Visual Relationship Detection." the Association for the Advancement of Artificial Intelligence (AAAI), 2019, pp. 8102-8109.

项目地址：https://github.com/Cadene/block.bootstrap.pytorch

二、文章导读

先看一下文章的摘要部分：

Multimodal representation learning is gaining more and more interest within the deep learning community. While bilinear models provide an interesting framework to find subtle combination of modalities, their number of parameters grows quadratically with the input dimensions, making their practical implementation within classical deep learning pipelines challenging. In this paper, we introduce BLOCK, a new multimodal fusion based on the block-superdiagonal tensor decomposition. It leverages the notion of block-term ranks, which generalizes both concepts of rank and mode ranks for tensors, already used for multimodal fusion. It allows to define new ways for optimizing the tradeoff between the expressiveness and complexity of the fusion model, and is able to represent very fine interactions between modalities while maintaining powerful mono-modal representations. We demonstrate the practical interest of our fusion model by using BLOCK for two challenging tasks: Visual Question Answering (VQA) and Visual Relationship Detection (VRD), where we design end-to-end learnable architectures for representing relevant interactions between modalities. Through extensive experiments, we show that BLOCK compares favorably with respect to state-of-the-art multimodal fusion models for both VQA and VRD tasks. Our code is available at https://github.com/Cadene/block.bootstrap.pytorch.

多模态表示学习（Multimodal representation learning）一直是个热点。双线性模型能为模态的融合提供很好的框架，但是参数数量却随着输入维度呈平方式增长。这篇文章，作者提出了BLOCK模型，即一种新的多模态融合模型，它基于块-超对角张量分解技术。它使用了块项秩（block-term ranks）的概念，能够对张量的“秩”和“模态秩”的概念进行泛化，已多用于多模态融合。BLOCK定义一种新的方式，用于优化融合模型的表达性和复杂性之间的平衡，并且能够表示模态间的精确交互，同时还保留单模态表示。然后作者将 BLOCK用在了VQA和VRD中，结果表明BLOCK达到了最好的模态融合效果。

三、文章详细介绍

常见的一些多模态交互任务包括visual question answering，visual relationship detection，cross-modal retrieval，social-media post classification等。对于单模态任务，网络结构一般都可以视作一个线性结构，即输入x对应输出y，而多模态任务，比如两个模态，就需要扩展为两个线性模型来处理了。但是双线性模型的参数会随着输入的维度呈平方级增长，目前面临的主要问题就是减少参数数量。

对于线性模型，可以通过约束线性模型矩阵的秩来实现，不幸的是，对于双线性模型会复杂的很多，因为它涉及到了多重线性代数的概念。

这篇文章，作者针对此问题，提出一种端到端的双线性模型，即BLOCK（Block Superdiagonal Fusion framework），用于多模态的表示。BLOCK基于块项张量（block-term tensor）分解，这种分解技术使用了块项秩（block-term）的概念来定义张量的复杂度。复杂度的分析能够提供一种新的方式，以控制融合模型的表示和复杂度之间的平衡。

最后作者将该模型用于了两个VQA数据集和一个VRD数据集。

1.BLOCK融合模型（BLOCK fusion model）

假设一个双线性模型有两个输入x1和x2，那么利用张量T将它们投影在K维空间中可以表示为（1）式中的y：

这里y的每一个元素其实都是一个输入的二次项构成。

BLOCK model：

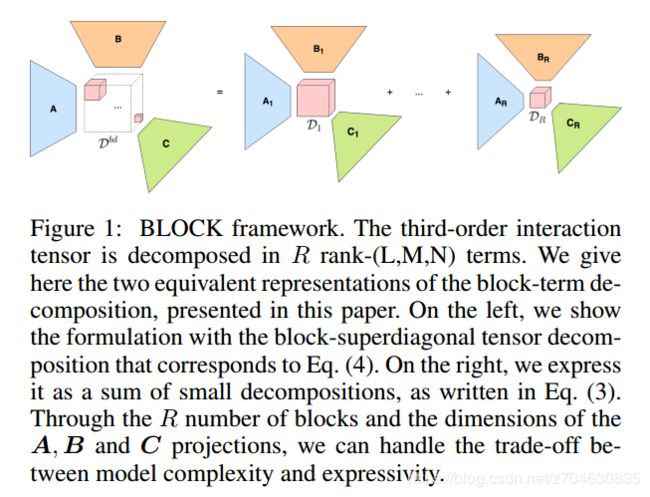
为了减少参数，将张量T使用block-term分解：

这种分解就被称为block-term，它可以写成上式（4）的形式。该分解可以如下图所示（这里就是一个三维的tensor分解示意图，三维的可以看做A和B两个维度再加上C这个维度构成一个三维的tensor）：

然后再进一步将两个输入的投影合并：

每一个块得到的向量Zr进行连接，得到z向量，最终的预测向量就是y=Cz。

2. BLOCK用于VQA

这里作者举了很多模型。VQA一般预测答案是其视为分类问题，对融合好的特征进行分类。在MCB模型中（Fukui et al. 2016），使用了sketching技术简化了双线性交互。目前的众多的模型处理复杂度的问题都是采用张量分解的方式，比如MLB (Kim et al. 2017)和MUTAN (BenYounes et al. 2017)使用了CP分解和Tucker分解。在MFB(Yu et al. 2017b)中，张量看做矩阵的叠加。在MFH (Yu et al. 2018)中，使用了多个MFB块进行串联。这些工作都是将融合策略嵌入到了网络中。本文作者提出了BLOCK，可用VQA进行多模态融合，且降低模型参数数量。

• Fukui, A., Park, D.H., Yang, D., Rohrbach, A., Darrell, T. and Rohrbach, M. (2016) Multimodal Compact Bilinear Pooling for Visual Question Answering and Visual Grounding. Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing, Austin, TX, November 2016, 457-468.
  https://doi.org/10.18653/v1/D16-1044
• Kim, J.-H.; On, K. W.; Lim, W.; Kim, J.; Ha, J.-W.; and Zhang, B.-T. 2017. Hadamard Product for Low-rank Bilinear Pooling. In ICLR
• Ben-Younes, H.; Cadene, R.; Thome, N.; and Cord, M. ` 2017. Mutan: Multimodal tucker fusion for visual question answering. ICCV.
• Yu, Z.; Yu, J.; Fan, J.; and Tao, D. 2017b. Multi-modal factorized bilinear pooling with co-attention learning for visual question answering. ICCV.
• Yu, Z.; Yu, J.; Xiang, C.; Fan, J.; and Tao, D. 2018. Beyond bilinear: Generalized multi-modal factorized highorder pooling for visual question answering. IEEE TNNLS.

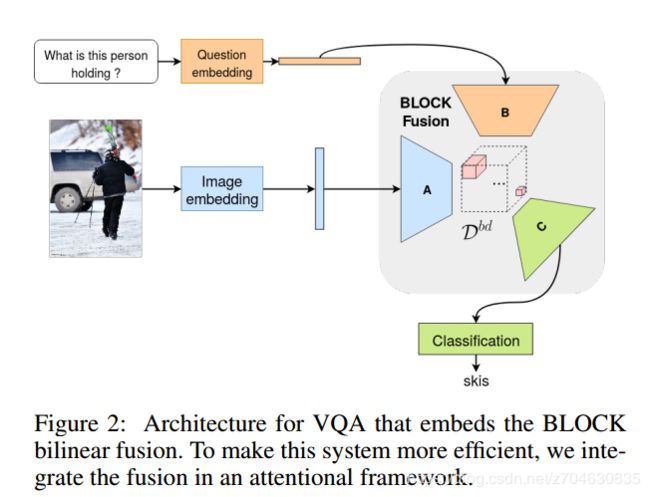
VQA结构：本文的VQA结构基于Fukui et al. 2016文章中的注意力结构，结合BLOCK的VQA的模型结构如下图所示：

其中图像特征根据文献Teney et al. 2018，使用的是Bottom-up image features，该特征包含了检测出的目标以及他们的表示。问题嵌入使用的是Skip-thought编码，先产生一个问题向量，然后再根据Yu et al. 2018的工作，再生成问题的表示。之后再使用BLOCK来融合图像表示和问题表示，另外问题向量再用于引导视觉注意力。另外一些模型参数这里就不再介绍了。

• Teney, D.; Anderson, P.; He, X.; and van den Hengel, A. 2018. Tips and tricks for visual question answering: Learnings from the 2017 challenge. In CVPR.

融合分析：作者将提出的BLOCK与以下8种VQA的融合方式进行了比较：

– (1) the two vectors are projected on a common space, and their summation is projected to predict the answer; （将两个向量投影在同一个空间中，求和后再预测答案）

– (2) the vectors are concatenated and passed at the input of a 3-layer MLP; （将两个向量连接然后再传入三层的感知器中）

– (3) a bilinear interaction based on a count-sketching technique that projects the outer product of between inputs on a multimodal space;（基于count-sketching技术的双线性交互，将输入之间的乘积映射到多模态空间中）

– (4) a bilinear interaction where the tensor is expressed as a Tucker decomposition; （双线性交互中的张量用塔克分解）

– (5) a bilinear interaction where the tensor is expressed as a CP decomposition; （双线性交互中的张量用CP分解）

– (6) a bilinear interaction where each 3rd mode slice matrix of the tensor is constrained by its rank; （双线性交互中用秩约束张量的每个第三模态切片矩阵？？？）

– (7) a bilinear interaction where the tensor is expressed as a Tucker decomposition, and where its core tensor has the same rank constraint as (6); （双线性交互中张量表示为塔克分解，其中核心张量与（6）中的秩约束相同）

– (8) a higher order fusion composed of cascaded (6); （串联的（6）组成的高次融合）

– (9) our BLOCK fusion. （BLOCK）

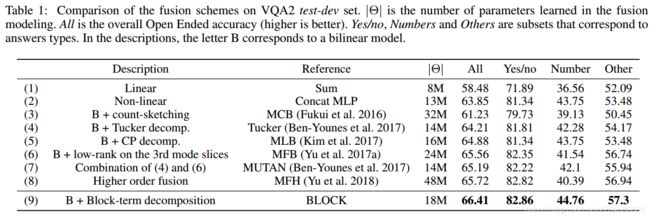
融合的实验结果如下图所示：

（1）这种简单求和的方法得分最低；（2）尽管也使用了非线性结构，但是表现也不好，因为尽管MLP能够区分两种不同模态，但是实际应用中并不那么容易，而最好的表现方法也应该是基于双线性结构的；（3）中使用了随机投影的简化双线性模型，由于count-sketching技术，该模型存在效率问题；而这类问题则可以通过张量分解来缓解，（9）通过泛化塔克分解和CP分解，达到了最好的结果。

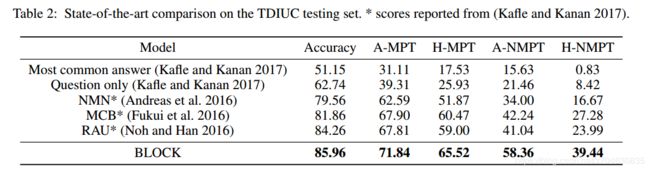
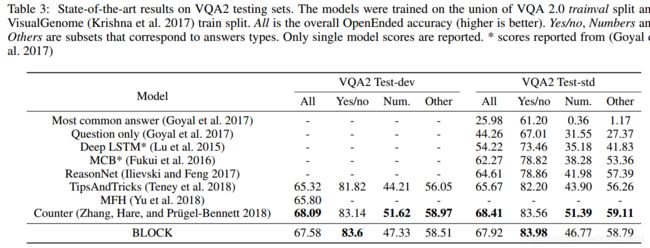
VQA的比较：作者基于VQA 2.0和TDIUC数据集来比较模型效率。实验结果就是表2和表3中的内容：

实验后面的部分是关于VRD的，就不多做介绍了。

四、小结