密度聚类（一）DBSCAN和python实现

密度聚类

密度聚类算法假设聚类结构能通过样本分布的紧密程度确定，通常这类算法从样本密度的角度考虑样本之间的可连接性，并基于可连接样本不断扩展聚类簇以获得最终的聚类结果。

DBSCAN

DBSCAN基于一组“邻域”参数刻画样本分布的紧密程度：
这组参数是 $\left\{ϵ,MinPts\right\}$ ,
$ϵ$表示与目标点的距离阈值
$MinPts$表示处于距离阈值内的样本个数阈值

下面介绍几个概念：

给定一个样本集D={x1,x2,…}

• $ϵ$邻域：对于D中的某个样本x，样本集D中与x的距离小于$ϵ$的样本集合叫做$ϵ$邻域。
• 核心对象：若x的$ϵ$邻域包含的样本数大于等于$MinPts$，则认为x为一个核心对象
• 密度直达：若xj位于xi的$ϵ$邻域，且xi为一个核心对象，则称xj由xi密度直达
• 密度可达：对于xi和xj，存在一个序列xi，x1，x2,…,xn，xj，序列两两之间是密度直达的，则xi和xj是密度可达的
• 密度相连：对于xi和xj，若存在xk使得xi和xj均由xk密度可达，则xi和xj密度相连

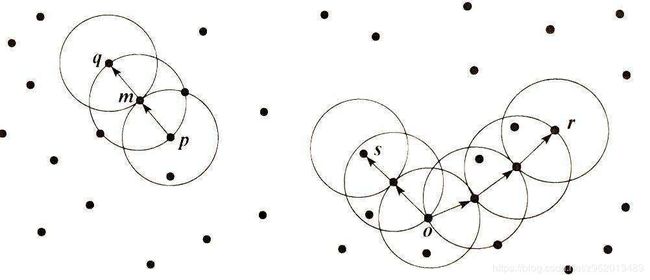
上图若$ϵ$为3，则左边m是核心对象，则q点和p点是密度可达
右图s和r是密度相连的，也是密度可达的

根据上面的概念，定义DBSCAN的簇：由密度可达关系导出的最大的密度相连样本集合。

给出DBSCAN的伪代码：

DBSCAN的主要优点有：

1） 可以对任意形状的稠密数据集进行聚类，相对的，K-Means之类的聚类算法一般只适用于凸数据集。

2） 可以在聚类的同时发现异常点，对数据集中的异常点不敏感。

3） 聚类结果没有偏倚，相对的，K-Means之类的聚类算法初始值对聚类结果有很大影响。

DBSCAN的主要缺点有：

1）如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合。

2） 如果样本集较大时，聚类收敛时间较长，此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。

3） 调参相对于传统的K-Means之类的聚类算法稍复杂，主要需要对距离阈值ϵ，邻域样本数阈值MinPts联合调参，不同的参数组合对最后的聚类效果有较大影响。

python3.6实现

# -*- coding: gbk -*-

import numpy as np
import matplotlib.pyplot as plt
import copy
from sklearn.datasets import make_moons
from sklearn.datasets.samples_generator import make_blobs
import random


class DBSCAN():
    def __init__(self, epsilon, MinPts):
        self.epsilon = epsilon
        self.MinPts = MinPts

    def dist(self, x1, x2):
        return np.linalg.norm(x1 - x2)

    def getCoreObjectSet(self, X):
        N = X.shape[0]
        Dist = np.eye(N) * 9999999
        CoreObjectIndex = []
        for i in range(N):
            for j in range(N):
                if i > j:
                    Dist[i][j] = self.dist(X[i], X[j])
        for i in range(N):
            for j in range(N):
                if i < j:
                    Dist[i][j] = Dist[j][i]
        for i in range(N):
            # 获取对象周围小于epsilon的点的个数
            dist = Dist[i]
            num = dist[dist < self.epsilon].shape[0]
            if num >= self.MinPts:
                CoreObjectIndex.append(i)
        return np.array(CoreObjectIndex), Dist

    def element_delete(self, a, b):
        if isinstance(b, np.ndarray) == False:
            b = np.array([b])
        for i in range(b.shape[0]):
            index = np.where(a == b[i])
            a = np.delete(a, index[0])
        return a

    def fit(self, X):
        N = X.shape[0]
        CoreObjectIndex, Dist = self.getCoreObjectSet(X)
        self.k = 0
        self.C = []
        UnvisitedObjectIndex = np.arange(N)

        while(CoreObjectIndex.shape[0] != 0):
            old_UnvisitedObjectIndex = copy.deepcopy(
                UnvisitedObjectIndex)  # 记录当前未访问的样本id
            OriginIndex = np.random.choice(
                CoreObjectIndex.shape[0], 1, replace=False)  # 随机选取一个核心对象
            Queue = np.array([-1, CoreObjectIndex[OriginIndex]])  # 初始化队列

            CoreObjectIndex = self.element_delete(
                CoreObjectIndex, CoreObjectIndex[OriginIndex])  # 将核心对象id从id集合中除去
            while(Queue.shape[0] != 1):
                # 取出队列中首个样本id
                index = Queue[0]
                if index == -1:
                    Queue = np.delete(Queue, 0)
                    Queue = np.append(Queue, -1)
                    continue

                Queue = self.element_delete(Queue, index)
                index = int(index)
                DistWithOthers = Dist[index]
                OthersIndex = np.where(DistWithOthers < self.epsilon)[0]
                num = OthersIndex.shape[0]
                if num >= self.MinPts:
                    delta = list(set(OthersIndex).intersection(
                        set(UnvisitedObjectIndex)))  # 取核心对象内的样本和未访问样本集合的交集
                    delta = np.array(delta)
                    Queue = np.append(Queue, delta)
                    UnvisitedObjectIndex = self.element_delete(
                        UnvisitedObjectIndex, delta)

            self.k += 1
            self.C.append(
                self.element_delete(old_UnvisitedObjectIndex, UnvisitedObjectIndex))
            CoreObjectIndex = self.element_delete(
                CoreObjectIndex, self.C[self.k - 1])
        print("共有{} 个簇".format(self.k))

        Y = np.zeros(X.shape[0])
        for i in range(self.k):
            Y[self.C[i]] = i + 3

        return Y

    def plt_show(self, X, Y, pre_Y, name=0):
        if X.shape[1] == 2:
            fig = plt.figure(name)
            plt.subplot(211)
            plt.scatter(X[:, 0], X[:, 1], marker='o', c=Y)
            plt.subplot(212)
            plt.scatter(X[:, 0], X[:, 1], marker='o', c=pre_Y)
            plt.colorbar()
        else:
            print('error arg')


if __name__ == '__main__':

    center = [[1, 1], [-1, -1], [1, -1]]
    cluster_std = 0.35
    X1, Y1 = make_blobs(n_samples=300, centers=center,
                        n_features=2, cluster_std=cluster_std, random_state=1)

    dbscan1 = DBSCAN(epsilon=0.4, MinPts=5)
    pre_Y1 = dbscan1.fit(X1)
    dbscan1.plt_show(X1, Y1, pre_Y1, name=1)

    center = [[1, 1], [-1, -1], [2, -2]]
    cluster_std = [0.35, 0.1, 0.8]
    X2, Y2 = make_blobs(n_samples=300, centers=center,
                        n_features=2, cluster_std=cluster_std, random_state=1)

    dbscan2 = DBSCAN(epsilon=0.4, MinPts=5)
    pre_Y2 = dbscan2.fit(X2)
    dbscan2.plt_show(X2, Y2, pre_Y2, name=2)

    X3, Y3 = make_moons(n_samples=1000, noise=0.1)
    dbscan3 = DBSCAN(epsilon=0.1, MinPts=5)
    pre_Y3 = dbscan3.fit(X3)
    dbscan3.plt_show(X3, Y3, pre_Y3, name=3)

    plt.show()

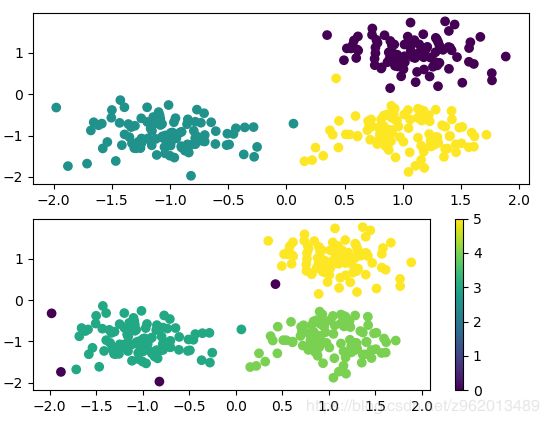
对于3类密度均匀的类别样本集，DBSCAN可以很好的聚类，图中紫色的点为异常点。

对于3类密度不均匀的类别样本集，DBSCAN的聚类效果有点差，黄色类别的样本集中出现了很多异常点。

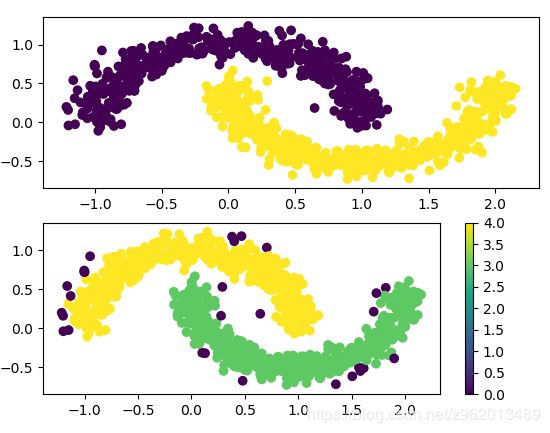
对于不是高斯分布的样本集，密度聚类的效果比原型聚类要强很多

参考文献

《机器学习》周志华
https://www.cnblogs.com/pinard/p/6208966.html