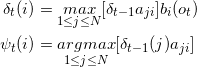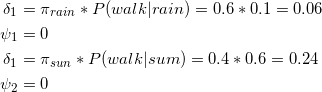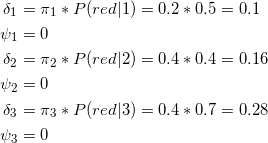HMM——维特比算法(Viterbi algorithm)
1. 前言
维特比算法针对HMM第三个问题,即解码或者预测问题,寻找最可能的隐藏状态序列:
对于一个特殊的隐马尔可夫模型(HMM)及一个相应的观察序列,找到生成此序列最可能的隐藏状态序列。
也就是说给定了HMM的模型参数和一个观测序列,计算一系列的隐状态,使得此观察序列的出现可能最大,即最大化P(隐状态 | 观测序列),给定观测序列,求最可能的对应的隐状态序列。
实际上解决此问题,在《统计学习方法》中给出了两种解法,一个是近似算法,另一个就是维特比算法(Viterbi algorithm)
2. 近似算法
思路:计算每一时刻最有可能出现的隐状态,从而得到一个状态序列作为预测结果。
算法:给定HMM模型参数λ和观测序列O,在时刻 t 处于状态qi的概率是:
则每一时刻t 最有可能的状态是
![]()
感觉很类似于贪婪算法,每一个时间点计算一次,取最大的。
优点是计算简单;而缺点就很明显了,没有考虑时序关系,不能保证预测的状态序列整体上是最优可能的状态序列,预测的状态序列可能有实际不发生的部分。
3. 维特比算法
利用动态规划求解概率最大的路径,一条路径一个状态序列。
动态规划求解最优路径专责:如果最优路径在某时刻t 通过节点i,那么这条路径从节点 i 到终点的部分路径,在节点 i 到终点的路径中,必须是最优的。
通过这种原理就可以从t=1时刻开始,不断向后递推到下一个状态的路径的最大概率,直到在最后到达最终的最优路径终点,然后依据终点回溯到起始点,这样就能得到最优路径。
具体过程:(《李航统计学习》)
输入:模型参数λ和观测序列![]()
输出:最优的隐状态路径![]()
(1) 第一层所有的N中状态概率
(2) 逐渐递推到t=2,3,...,.T
第一个式子是记录递推到 t 时刻时候,最优路径经过的所有结点的联合概率。
第二个式子是记录到底到达的是哪个节点,即 t 时刻的哪个隐状态
其实这一步说白了计算时间和前向计算差不多,只不过把前向计算的状态加和换成了取max值
(3) 终止
(4) 回溯最优路径,t= T-1,T-2,...,1
![]()
4. 维特比算法实例
4.1 天气的实例
摘自知乎上的一个实例:https://www.zhihu.com/question/20962240
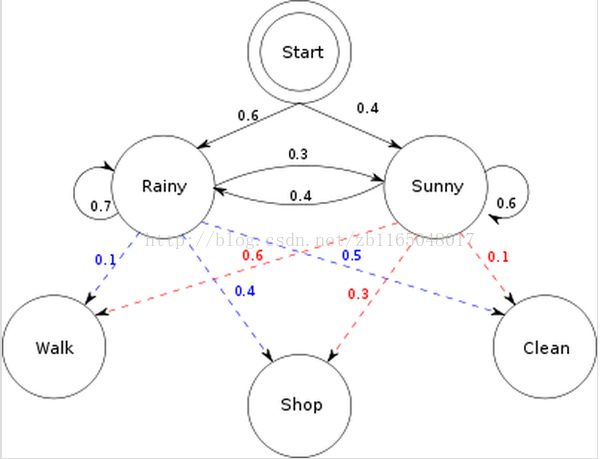
这张图就告诉了我们HMM的模型参数
初始概率π=[ 0.6 0.4]
转移概率(天气(隐状态)之间互相转移)
| rain | sun | |
| rain | 0.7 | 0.3 |
| sun | 0.4 | 0.6 |
混淆矩阵(每种天气(隐状态)对应行为(可观测)的概率)
| walk | shop | clean | |
| rain | 0.1 | 0.4 | 0.5 |
| sun | 0.6 | 0.3 | 0.1 |
已知模型参数,以及三天的行为(walk,shop,clean)
求解:三天对应最可能的天气状态
解答:
【注】δ的下标不是代表第几天,而是当前天的第几个隐状态,注意,下面的每天的第二个δ下标都写错了,应该是δ2,因为不是用markdown写的,懒得改了,自己推导注意一下
①首先初始化,对于每一个天气状态,求当天对应行为的概率
初始化,即第一天不用找最大值,因为第一天哪里知道最可能的路径,路径是链接两个节点的,一个节点无法称为路径
②第一天到达第二天的路径概率
③第二天到第三天的路径概率
④回溯
找到最后一天最大的概率
![]()
发现第三天对应第一个状态的概率最大,而且此概率通过③中的ψ1是第二天的第一个状态ψ1到达第三天的第一个状态得到的,所以第二天对应的应该是第一个状态。
而到达第二天的第一个状态的最大概率是第一天的第二个状态,通过②中的ψ1能够看出来。
所以合起来就是第一天的第二个状态->第二天的第一个状态->第三天的第一个状态
即三天天气应该是(sun,rain,rain)
4.2 球与盒子的实例
依旧是前向算法中选择的实例,摘自《李航统计学习》
已知:三个盒子是隐状态,球的颜色是观测序列(红、白、红)
转移矩阵
| 1 | 2 | 3 | |
| 1 | 0.5 | 0.2 | 0.3 |
| 2 | 0.3 | 0.5 | 0.2 |
| 2 | 0.2 | 0.3 | 0.5 |
混淆矩阵
| red | white | |
| 1 | 0.5 | 0.5 |
| 2 | 0.4 | 0.6 |
| 3 | 0.7 | 0.3 |
初始概率:π=(0.2,0.4,0.4)
解答过程:
①初始化,拿到红球
②第二次 拿到白球的时候,路径概率
谢谢@征途开始 指出的问题,之前这里的公式写错了,排版的时候上传图片搞错了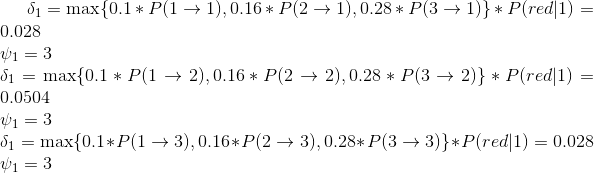
③第三次拿到红球时候,路径概率
④通过第三次拿的ψ ,找第三次拿最大的概率:ψ3=0.0147
对应的是第三个隐状态,然后看它对应从第二条路径中的哪一个转移过来的,看③中的ψ3=3,说明是第二个路径的第三个状态
然后查看第二个路径第三个状态对应的是从第一个状态的哪一个转移过来的,看②中的ψ3=3,说明是第一个路径的第三个状态
综上,隐状态的转移过程为(3,3,3)