递归面试题整理以及时间复杂度分析

   【摘要】  递归具有很多的优点，它可以将一个大的问题划分为小的子问题，然后再逐步细分，达到解决问题的目的。递归的实现借用了栈桢的建立和销毁，所以它是很方便的。但是递归也有一些缺点，比如说，如果递归调用太深，栈桢消耗过大，就会出现栈溢出的问题，因此，在我们使用递归之前，应该仔细考虑适不适合使用递归来解决这个问题。同时，递归深度太深，也会使得运算时间大大增加，所以递归的结论一般都是在理论的基础上的。这篇文章整理了我最近做过的关于递归的一些经典问题，希望对你们会有所帮助。

  这是要讲的六个面试题

     1.递归法求斐波那契数列

     2.递归计算n的k次方

     3.递归计算一个数字每一位相加的结果

     4.递归逆序输出字符串

     5.递归求字符串长度

     6.递归求阶乘

一.递归法求斐波那契数列

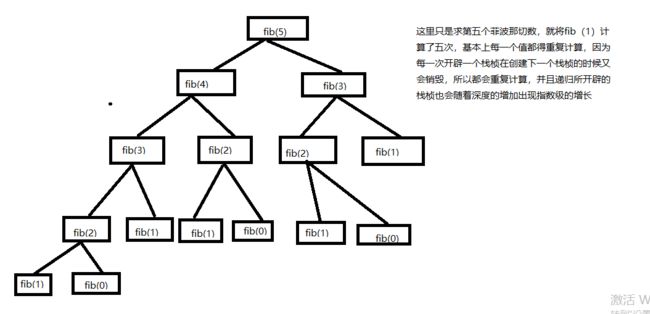
         在这里我先要说的是，递归法求菲波那切数列并不是一个很好的解决办法，如果你要问我为什么，其实前面也提到了，如果求第10个或者第20数的值，还好，但是如果要求第100个呢？这样做消耗的栈桢将会是很大的，我先拿一张图来大概表示一下栈桢的消耗过程

并且，随着递归次数越多，时间复杂度也会越高，综合这两点，我觉得用循环来代替递归是很明智的选择。当然我也不是就说递归不好了，有时候用递归解决问题还是相当给力的。

菲波那切数列求值，思想就是每一个值都是前面两个数的和，因此放到递归里面就可以分解为子问题，求前两个数字的结果，就这样一直往前走，直到遇到1就返回，然后再把值一个个相加，得到最后的结果。

代码如下

#include
#include

int fabonaci(int i)
{
	if(i<=0)
		return 0;
	else if(i==1 ||i==2)
		return 1;
	else
		return(fabonaci(i-1)+fabonaci(i-2));
}
int main()
{
	int ret=0;
	int i=-2;
	ret=fabonaci(i);
    printf("fabponaci number i is %d\n",ret);


	system("pause");
	return 0;
}

二.递归计算n的k次方

      递归一般都是逆序思想，要求n的k次方，那就先求n的k-1次方，而要求n的k-1次方，就要求k-2次方，就这样一直给前走，直到求n的0次方为终止条件。而n的k次方就是k个n相乘，所以，只需要每次返回时乘上n就可以得到最终的结果

代码如下

#include
#include

int sqrt(int n,int k)
{
	if(k==0)
       return 1;
	else
		return n*sqrt(n ,k-1);
}
int main()
{
	int ret=0;
	int n=2;
	int k=3;
	ret=sqrt(n,k);
    printf("%d ^ %d=%d",n,k,ret);
	system("pause");
	return 0;
}

三.递归计算一个数字每一位相加的结果

     要想得到一个数字的每一位，最简单的办法就是%10 /10，如此反复几次，直到i==0为止，而要让每一位都相加，那就在 return 后面返回一个范围缩小的值 加上%10的值，当函数得到第一位数字时就开始返回结果，这个递归问题是线性的，所以栈桢消耗并不会很大

代码如下

#include
#include

int DigitSum(int i)
{
	
	if(i==0)
		return 0 ;
	else
	{
		if((i/10)>0)
		{
		printf("%d+",i%10);
		}
		else
        printf("%d",i%10);
		return (i%10+DigitSum(i/10));
	}
	   
}		
int main()
{
	int ret=0;
	int i=1729;
	ret=DigitSum(i);
	printf("=%d",ret);
	system("pause");
	return 0;
}

四.递归逆序输出字符串

      这个问题其实用递归也是很好解决的，原因就在于，递归的创建是逆思路进行的，它会把你要得到的结果在函数到达终止条件时开始返回，因此，你只需要定义一个指针，让它一直走到字符串的结束位置，然后开始打印字符串，这样屏幕上输出的字符串就一定是逆序的

代码如下

#include
#include

void reverse_string(char*s)
{
	if(*s =='\0')
	{
		s--;
		return ;
	}
	reverse_string(s+1);
	printf("%c ",*s);
}
    
int main()
{
	char *s="hello";
    reverse_string(s);

	system("pause");
	return 0;
}

五.递归求字符串长度

      一个字符串的长度等于每一个字符相加的结果，因此可以转化为子问题，要求整个的长度，就是要求少一位的字符串的长度加一，这样逐级建立栈桢，到达结束条件  \0 时就可以得到最终的结果

#include
#include

int my_strlen(char* s)
{
	if(*s == '\0')
		return 0;
	else
		return (1+my_strlen(s+1));//不要用s++，会栈溢出
}

int main()
{
	char s[]="sfgdsfggdsfgd";
	int ret;
	ret=my_strlen(s);
    printf("字符串的长度为：%d\n",ret);


	system("pause");
	return 0;
}

六.递归求阶乘

       求一个数的阶乘，就是求从一开始一直累乘直到乘自身为止，这样也可以转化为递归的子问题，比如说要求5的阶乘，可以转化为 求 5*f(5-1)的问题，而要求f（4）就可以转化为求4*f(3),这样一直递归，直到乘1，然后就可以返回结果并且返回了

代码如下

#include
#include

int Factorial(int i)
{
	if(i==0)
		return 1;
	else
		return i*(Factorial(i-1));
}

int main()
{
	int ret=0;
	int i=5;
	ret=Factorial(i);
	printf("%d的阶乘为：%d\n",i,ret);

	system("pause"); 
	return 0;
}

   

总结：递归可以简化问题，但同时它本身也有很多问题，递归过于深入就会导致时间复杂度大大增加，栈桢开销指数级增长，所以，我觉得求一般的小问题使用递归是完全可行的，但是遇到复杂，数据量很大的问题，建议还是用循环模拟栈桢的创建来解决更复杂的问题吧。

       谢谢你们可以看到这里，本文可能有些地方有些赘述，因为我也是初学者，所以有纰漏之处欢迎指正，我一定虚心接受