算法:Climbing Stairs(爬楼梯) 6种解法
说明
算法:Climbing Stairs(爬楼梯)
LeetCode地址:https://leetcode.com/problems/climbing-stairs/
题目:
You are climbing a stair case. It takes n steps to reach to the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
Note: Given n will be a positive integer.
Example 1:
Input: 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
Example 2:
Input: 3
Output: 3
Explanation: There are three ways to climb to the top.
3. 1 step + 1 step + 1 step
4. 1 step + 2 steps
5. 2 steps + 1 step
解题思路1 - 递归
爬楼梯直接思路递归法,登顶的最后一步有两种走法,也就是1步,后者2步。
所以可以得出公式f(n) = f(n-1) + f(n-2).
注意初始条件
- f(1) = 1;
- f(2) = 2;
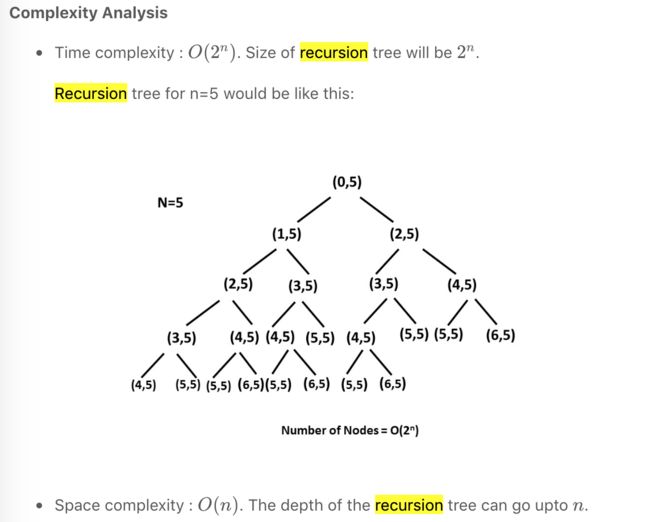
复杂度分析,时间复杂度为2^n。
因为有重复的数据多次计算,比如f(3), 每个大于3的都要重新计算一次。
递归函数还有个弊端,需要担心函数调用栈溢出。
代码实现1
public class ClimbingStairs {
public static int climbStairsWithRecursion(int n) {
if (n == 1) {
return 1;
} else if (n == 2) {
return 2;
} else {
return climbStairsWithRecursion(n - 1) + climbStairsWithRecursion(n - 2);
}
}
}
代码执行效率1
Runtime: 7107 ms, faster than 10.50% of Java online submissions for Climbing Stairs.
Memory Usage: 36.4 MB, less than 27.61% of Java online submissions for Climbing Stairs.
解题思路2 - 递归加缓存
递归执行效率太低真实原因,是因为数据重复计算,用数组memoryArray存储已经计算过得数据。
时间复杂度降低为O(n), 内存复杂度为O(n) .
代码实现2
public class ClimbingStairs {
public static int climbStairsWithRecursionMemory(int n) {
int[] memoryArray = new int[n + 1];
return subClimbStairsWithRecursionMemory(n - 1, memoryArray) + subClimbStairsWithRecursionMemory(n - 2, memoryArray);
}
public static int subClimbStairsWithRecursionMemory(int n, int[] memoryArray) {
if (n == 1) {
return 1;
} else if (n == 2) {
return 2;
} else {
if (memoryArray[n] > 0) {
return memoryArray[n];
}
memoryArray[n] = subClimbStairsWithRecursionMemory(n - 1, memoryArray) + subClimbStairsWithRecursionMemory(n - 2, memoryArray);
return memoryArray[n];
}
}
}
代码执行效率 2
Runtime: 2 ms, faster than 90.23% of Java online submissions for Climbing Stairs.
Memory Usage: 36.5 MB, less than 6.57% of Java online submissions for Climbing Stairs.
解题思路3 - 动态规划
担心递归会有函数调用指针栈溢出风险,既然有子函数解决问题方案,动态规划呼之即出。
递推公式:f(n) = f(n-1) + f(n-2)
时间复杂度降低为O(n), 内存复杂度为O(n) .
代码实现3
public class ClimbingStairs {
public static int climbStairsWithDynamic(int n) {
if (n == 1) {
return 1;
}
int dynamicArray[] = new int[n + 1];
dynamicArray[1] = 1;
dynamicArray[2] = 2;
for (int i = 3; i <= n; i++) {
dynamicArray[i] = dynamicArray[i - 1] + dynamicArray[i - 2];
}
return dynamicArray[n];
}
}
解题思路4 - Fibonacci
内存占用太高,公式很熟悉Fibonacci, 直接用3个变量就好,first, second, third。
递推公式:f(n) = f(n-1) + f(n-2)
时间复杂度降低为O(n), 内存复杂度为O(1) .
代码实现4
public class ClimbingStairs {
public static int climbStairsWithFibonacci(int n) {
if (n == 1) {
return 1;
}
int first = 1;
int second = 2;
for (int i = 3; i <= n; i++) {
int third = first + second;
first = second;
second =third;
}
return second;
}
}
解题思路5 - Fibonacci优化变量
内存占用太高,公式很熟悉Fibonacci, 变量是否还可以不用临时变量third呢,是可以的。
递推公式:f(n) = f(n-1) + f(n-2)
时间复杂度降低为O(n), 内存复杂度为O(1) .
代码实现5
public class ClimbingStairs {
public static int climbStairs(int n) {
int a = 1, b = 1;
while (--n > 0) {
b = b + a;
a = b - a;
}
return b;
}
}
代码执行效率 5
Runtime: 1 ms, faster than 100.00% of Java online submissions for Climbing Stairs.
Memory Usage: 36.6 MB, less than 5.01% of Java online submissions for Climbing Stairs.
解题思路6 - Fibonacci Formula
实际上时间复杂度O(n)不是最优。用公式的时间复杂度为 : O(log(n)). 因为开根号方法pow用时间log(n) .
空间复杂度O(1).
代码实现6
public class ClimbingStairs {
public static int climbStairsWithFibonacciFormula(int n) {
double sqrt5= Math.sqrt(5);
double fibn = Math.pow((1 + sqrt5) / 2, n + 1) - Math.pow((1 - sqrt5) / 2, n + 1);
return (int)(fibn / sqrt5);
}
}
代码执行效率 6
Runtime: 1 ms, faster than 100.00% of Java online submissions for Climbing Stairs.
Memory Usage: 36.4 MB, less than 24.93% of Java online submissions for Climbing Stairs.
测试
public static void main(String[] args) {
int n1 = 2;
System.out.println("input: " + n1 + " climbStairs: " + climbStairs(n1));
int n2 = 3;
System.out.println("input: " + n2 + " climbStairs: " + climbStairs(n2));
int n3 = 20;
System.out.println("input: " + n3 + " climbStairs: " + climbStairs(n3));
System.out.println("input: " + n3 + " climbStairsWithRecursion: " + climbStairsWithRecursion(n3));
System.out.println("input: " + n3 + " climbStairsWithRecursionMemory: " + climbStairsWithRecursionMemory(n3));
System.out.println("input: " + n3 + " climbStairsWithDynamic: " + climbStairsWithDynamic(n3));
System.out.println("input: " + n3 + " climbStairsWithFibonacci: " + climbStairsWithFibonacci(n3));
System.out.println("input: " + n3 + " climbStairsWithFibonacciFormula: " + climbStairsWithFibonacciFormula(n3));
}
结果
input: 2 climbStairs: 2
input: 3 climbStairs: 3
input: 20 climbStairs: 10946
input: 20 climbStairsWithRecursion: 10946
input: 20 climbStairsWithRecursionMemory: 10946
input: 20 climbStairsWithDynamic: 10946
input: 20 climbStairsWithFibonacci: 10946
input: 20 climbStairsWithFibonacciFormula: 10946
总结
爬楼梯由最初的递归解法,
降低时间复杂度用了缓存优化,
降低方法调用栈溢出用了动态规划,
降低空间复杂度用了斐波那系数Fibonacci,
最后竟然有O(log(n))的时间复杂度优化方法Fibonacci Formula。
前人的经验,我们的阶梯。
代码下载:
https://github.com/zgpeace/awesome-java-leetcode/blob/master/code/LeetCode/src/ClimbingStairs.java
参考:
https://leetcode.com/problems/climbing-stairs/solution/