论文阅读——《Wasserstein GAN》《Improved Training of Wasserstein GANs》

论文阅读之 Wasserstein GAN 和 Improved Training of Wasserstein GANs

本博客大部分内容参考了这两篇博客: 再读WGAN（链接已经失效）和令人拍案叫绝的Wasserstein GAN, 自己添加了或者删除了一些东西, 以及做了一些修改.

基础知识：

f-Divergence

原始GAN采用的是JS divergence来衡量两个分布之间的距离。事实上有一个统一的模式来衡量两个分布间的距离，它就是f-divergence。
假设$P$和$Q$是两个分布。$p(x)$和$q(x)$是对应样本$x$的概率，则：

$$D_f(P||Q)={\int }_{x}q(x)f(\frac{p(x)}{q(x)})dx$$
就是f-Divergence, 其中$f$需要满足: 1. 是凸函数, 2. $f(1)=0$.
可以看到对任意的$x$都有$p(x)=q(x)$, 则$D_f(P||Q)={\int }_{x}q(x)f(\frac{p(x)}{q(x)})dx=0$, 即两个分布相同的时候f-Divergence等于0.

想要让f-divergence能表示两个分布的距离, 不但要求当两个分布相同时距离是0, 还需要保证这个0是f-Divergence能取到的最小值, 证明如下:
由于$f(x)$是凸函数，则有下面的不等式：
$$D_f(P||Q)={\int }_{x}q(x)f(\frac{p(x)}{q(x)})dx\ge f({\int }_{x}q(x)\frac{p(x)}{q(x)}dx)=f(1)=0$$

Fenchel Conjugate

每个凸函数$f$都具备一个共轭函数$f^{\ast }$：
$$f^{\ast }(t)=\underset{x\in dom(f)}{\max }\{xt-f(x)\}$$
关于Fenchel Conjugate有两个性质：

1. 所有的凸函数f都有一个conjugate函数$f^{\ast }$;
2. $((f^{\ast }{)}^{\ast })=f$.

和GAN的联系

假设$f^{\ast }$是$f$的Fenchel Conjugate函数, 则由上面的式子可以得到:
$$f(x)=\underset{t\in dom(f^{\ast })}{\max }\{tx-f^{\ast }(t)\}$$
将这个$f$作为上面f-Divergence中的$f$, 代入f-Divergence的式子得到:
$$D_f(P||Q)={\int }_{x}q(x)f(\frac{p(x)}{q(x)})dx={\int }_{x}q(x)(\underset{t\in dom(f\ast )}{\max }\{\frac{p(x)}{q(x)}t-f^{\ast }(t)\})dx$$
此时我们如果构建一个函数$D(x)\in dom(f^{\ast })$, 即输入$x$, 输出在$f^{\ast }$的定义域中, 这样我们就能有$D(x)$代替$t$, 但是这种替换对原来的公式并不是等价的. 因为我们所能用$D(x)$找到的$t$并不是那个能够让$f$最大的那个$t$. 所以我们替换之后构造的函数永远要小于等于f-Divergence：
$$\begin{gathered} D_f(P||Q)\ge {\int }_{x}q(x)(\frac{p(x)}{q(x)}D(x)-f^{\ast }(D(x)))dx \\ ={\int }_{x}p(x)D(x)dx-{\int }_{x}q(x)f^{\ast }(D(x))dx \end{gathered}$$
这就相当于我们找到了一个$D_f(P||Q)$的下界。接下来，如果我们能找到一个让上面公式不等号右边最大的$D$, 那么如果我们在公式中采用了这个找到的$D$, 那就可以去逼近$D_f(P||Q)$, 即：
$$\begin{gathered} D_f(P||Q)\approx \underset{D}{\max }{\int }_{x}p(x)D(x)dx-{\int }_{x}q(x)f^{\ast }(D(x))dx \\ =\underset{D}{\max }\{{\mathbb{E}}_{x\sim P}[D(x)]-{\mathbb{E}}_{x\sim Q}[f^{\ast }(D(x))]\} \end{gathered}$$
上面公式的第二行是将前面的概率积分变成了期望. 然而我们在工程上没法真的去求期望, 所以一般的做法就是分别从$P$和$Q$中去抽样数据.
假设现在我们的$P$是$P_{d}ata$，$Q$是$P_G$，则公式变成：
$$D_f(P_{data}||P_G)=\underset{D}{\max }{\mathbb{E}}_{x\sim P_{data}}[D(x)]-{\mathbb{E}}_{x\sim P_G}[f^{\ast }(D(x))]$$
但实际上想要将f-Divergence用在GAN中是不可能的，因为我们并不知道$P_{data}$和$P_G$的表达式. 所以我们这一路的公式推导, 最终得到的公式只需要我们简单地从$P_{data}$和$P_G$中采样就可以计算得到f-Divergence. 而不再需要知道这两个分布的表达式即可计算.

接下来，假如我们想要去寻找一个能让这个距离最小的$P_G$，则这个G应该是:
$$\begin{gathered} G^{\ast }=\arg \underset{G}{\min }{D}_f(P_{data}||P_G) \\ =\arg \underset{G}{\min }\underset{D}{\max }{\mathbb{E}}_{x\sim P_{data}}[D(x)]-{\mathbb{E}}_{x\sim P_G}[f^{\ast }(D(x))] \\ =\arg \underset{G}{\min }\underset{D}{\max }V(G,D) \end{gathered}$$

WGAN

前面我们介绍了使用f-Divergence来将“距离”定义到一个统一框架之中的方法. 而Fenchel Conjugate则将这个f-Divergence与GAN联系在一起。这么做的目的在于, 我们只要能找到一个符合f-Divergence要求的函数，就能产生一个距离的度量, 从而定义一种不同的GAN。

原生GAN的问题

对于原生的GAN来说, 选择特定的度量函数之后, 会导致目标函数变成生成分布与真是分布的JS divergence. 但是这个divergence有很多问题. 比如说一个最严重的问题就是当两个分布之间完全没有重叠时, 分布间距离的大小并不会直接反映在divergence上. 这对基于迭代的优化算法是个致命问题.

根据原始GAN定义的判别器loss, 我们可以得到最优判别器的形式; 而在最优判别器的下, 我们可以把原始GAN定义的生成器loss等价变换为最小化真实分布$P_r$与生成分布$P_g$之间的JS散度. 我们越训练判别器, 它就越接近最优, 最小化生成器的loss也就会越近似于最小化$P_r$和$P_g$之间的JS散度.

问题就出在这个JS散度上. 我们会希望如果两个分布之间越接近它们的JS散度越小, 我们通过优化JS散度就能将$P_g$“拉向”$P_r$, 最终以假乱真. 这个希望在两个分布有所重叠的时候是成立的, 但是如果两个分布完全没有重叠的部分, 或者它们重叠的部分可忽略(下面解释什么叫可忽略), 它们的JS散度是多少呢?
答案是$log2$, 因为对于任意一个x只有四种可能:
$P_1(x)=0且P_2(x)=0$
$P_1(x)\ne 0且P_2(x)\ne 0$
$P_1(x)=0且P_2(x)\ne 0$
$P_1(x)\ne 0且P_2(x)=0$
第一种对计算JS散度无贡献, 第二种情况由于重叠部分可忽略所以贡献也为0, 第三种情况对公式7右边第一个项的贡献是$\log \frac{P_2}{\frac{1}{2}(P_2+0)}=\log 2$, 第四种情况与之类似, 所以最终$JS(P_1||P_2)=\log 2$.

换句话说, 无论$P_r$跟$P_g$是远在天边, 还是近在眼前, 只要它们俩没有一点重叠或者重叠部分可忽略, JS散度就固定是常数$\log 2$, 而这对于梯度下降方法意味着——梯度为0! 此时对于最优判别器来说, 生成器肯定是得不到一丁点梯度信息的; 即使对于接近最优的判别器来说, 生成器也有很大机会面临梯度消失的问题.

但是$P_r$与$P_g$不重叠或重叠部分可忽略的可能性有多大? 不严谨的答案是: 非常大. 比较严谨的答案是：当$P_r$与$P_g$的支撑集(support)是高维空间中的低维流形(manifold)时, $P_r$与$P_g$重叠部分测度(measure) 为0的概率为1.

论文里面针对这个也做了相应的实验:

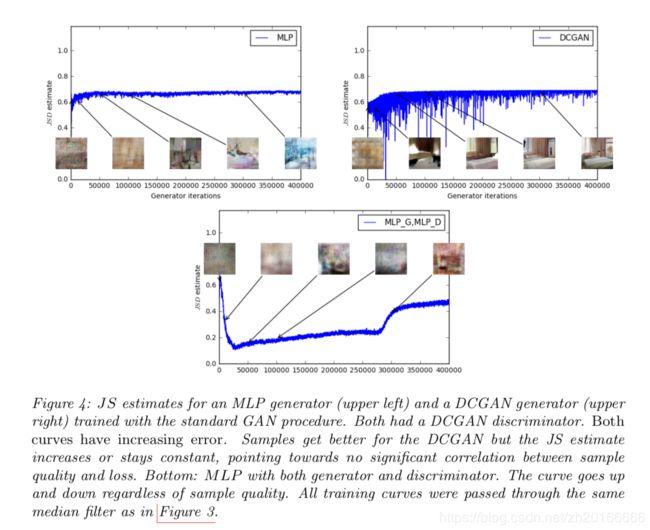
这个图的大致意思是作者用不同的网络结构做了实验, 发现随着迭代次数的增加, 生成图像的质量在提高, 但是真实数据和生成数据之间的JS散度却增加了或者是为一个常数, 这就从实验上验证了原来的GAN利用JS散度来学习的问题.

Earth Mover’s Distance

假设我们有下面的两个分布:

如何将P上的内容“匀一匀”得到Q呢? 比如说把最高的哪一条分开一部分分到其他地方? 这或许是一种解决方案:

但是显然除此之外还有很多种方法, 例如:

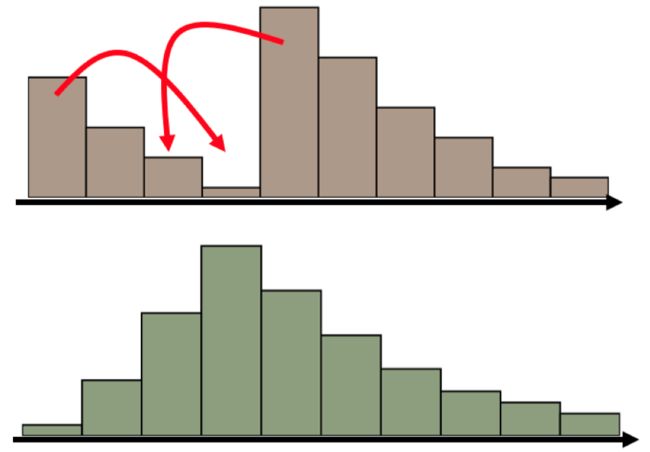
既然移动的方法有很多种, 如果每一种都表示了一种代价, 那么显然有“好”方法, 就会有“坏”方法. 假设我们衡量移动方法好坏的总代价是“移动的数量”X“移动的距离”. 那这两个移动的方案肯定是能分出优劣的.当我们用分布Q上不同颜色的色块对应分布P的相应位置, 就可以将最好的移动方案画成下面这个样子:

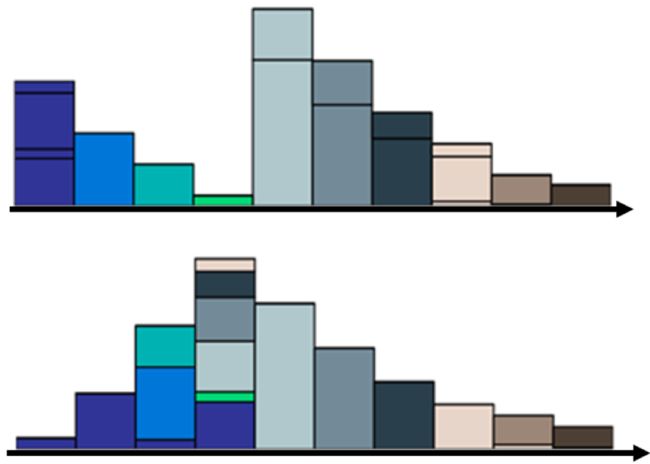
我们可以将这个变化画成一个矩阵:

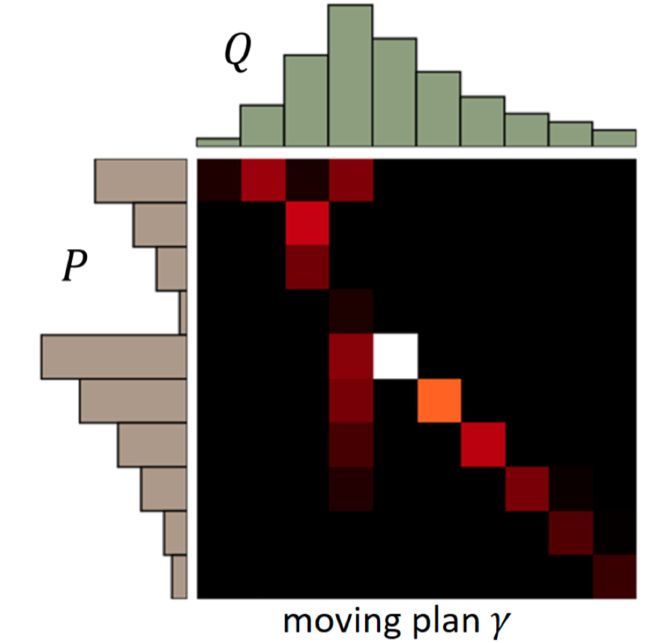
对于每一个移动方案$\gamma$, 都能有这样一个矩阵. 矩阵的每一行表示分布$P$的一个特定位置. 该行中的每一列表示需要将该行的内容移动到分布$Q$对应位置的数量. 即矩阵中的一个元素$(x_p,x_q)$表示从$P(x_p)$移动到$Q(x_q)$的数量。

而对于方案$\gamma$我们可以定义一个平均移动距离(Average distance of a plan $\gamma$):
$$B(\gamma )=\sum _{x_p,x_q}\gamma (x_p,x_q)||x_p-x_q||$$
而Earth Mover’s Distance就是指所有方案中平均移动距离最小的那个方案：
$$W(P,Q)=\underset{\gamma \in \Pi }{\min }B(\gamma )$$
其中$\Pi$是所有可能的方案.
作者在论文中也通过实验说明了EM距离比JS散度更能反应连个分布间的距离:

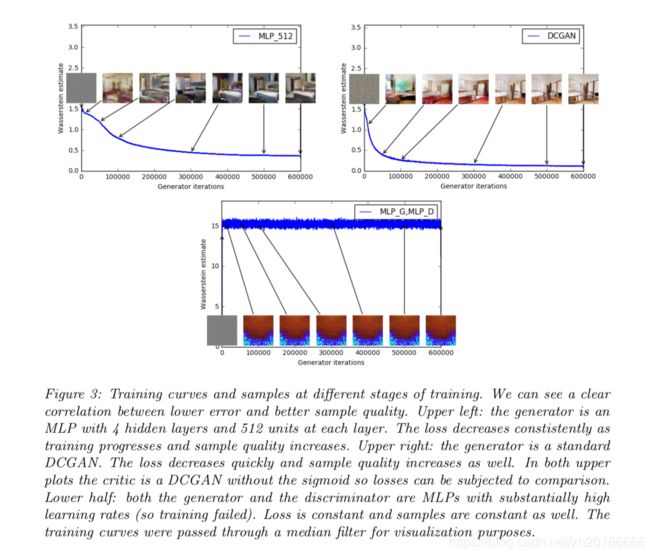
上面两幅图说明在训练过程中, 随着EM距离的减小, 生成图片的质量越来越高; 而下面这幅图b表示EM距离为一个常数, 生成的图片也就很差.

EM距离与GAN结合

回忆一下f-Divergence：
$$D_f(P_{data}||P_G)=\underset{D}{\max }{\mathbb{E}}_{x\sim P_{data}}[D(x)]-{\mathbb{E}}_{x\sim P_G}[f^{\ast }(D(x))]$$
而WGAN的文章中写到，EM距离也可以类似f-Divergence，用一个式子表示出来：
$$W(P_{data},P_G)=\underset{D\in 1-Lipschitz}{\max }{\mathbb{E}}_{x\sim P_{data}}[D(x)]-{\mathbb{E}}_{x\sim P_G}[D(x)]$$
公式中1-Lipschitz表示了一个函数集. 当$f$是一个Lipschitz函数时，它应该受到以下约束:
$$||f(x_1)-f(x_2)||\le K||x_1-x_2||$$
当K=1时，这个函数就是1-Lipschitz函数。
为什么要限制生成器D时1-Lipschitz函数呢
假设我们现在有两个一维的分布, $x_1$和$x_2$的距离是$d$, 显然他们之间的EM距离也是$d$:

此时如果我们想要去优化
$$W(P_{data},P_G)=\underset{D\in 1-Lipschitz}{\max }\{{\mathbb{E}}_{x\sim P_{data}}[D(x)]-{\mathbb{E}}_{x\sim P_G}[D(x)]$$
只需要让$D(x_1)=+\infty$，而让$D(x_2)=-\infty$就可以了. 也就是说，如果不加上1-Lipschitz的限制的话, 只需要让判别器判断$P_{data}$时大小是正无穷, 判断PG时是负无穷就足够了. 这样的判别器可能会导致训练起来非常困难: 判别器区分能力太强, 很难驱使生成器让生成分布适应数据分布.

这个时候我们加上了这个限制, 也就是说$||D(x_1)-D(x_2)||\le ||x_1-x_2||=d$. 此时如果我们想要满足上面的优化目标的话, 就可以让$D(x_1)=k+d$, 让$D(x_2)=k$. 其中$k$具体是什么无所谓, 关键是我们通过$d$将判别器在不同分布上的结果限制在了一个较小的范围中. 传统的GAN所使用的判别器是一个最终经过sigmoid输出的神经网络, 它的输出曲线肯定是一个S型. 在真实分布附近是1, 在生成分布附近是0. 而现在我们对判别器施加了这个限制, 同时不再在最后一层使用sigmoid, 它有可能是任何形状的线段, 只要能让$D(x_1)-D(x_2)\le d$即可. 如下图所示:

这样做的好处显而易见. 传统GAN的判别器是有饱和区的, 而现在的GAN如果是一条直线, 那就能在训练过程中无差别地提供一个有意义的梯度.说了这么多, WGAN主要的变化在这两点:

1. 不要用sigmoid输出;
2. 换成受限的1-Lipschitz来实现一个类似sigmoid的“范围限制”功能.

1-Lipschitz限制应该如何施加?
文章中所用的方法是截断权重.

WGAN的伪代码如下:

• 初始化D的${\theta }_d$和G的${\theta }_g$
• 在每一个训练循环进行：
  • 从数据分布$P_{data(x)}$中采样m个样本$\{x_1,x_2,\dots ,x_m\}$
  • 从先验噪声分布$P_{prior(z)}$中采样m个样本$\{z_1,z_2,\dots ,z_m\}$
  • 将这些噪声样本输入生成器G，得到生成样本$\{{\tilde{x}}_1,{\tilde{x}}_2,\dots ,{\tilde{x}}_m\},{\tilde{x}}_i=G(z_i)$
  • 更新判别器的参数θd，即最大化：
    • $\tilde{V}=\frac{1}{m}{\sum }_{i=1}^{m}D(x_i)-\frac{1}{m}{\sum }_{i=1}^{m}D({\tilde{x}}_i)$
    • ${\theta }_d\leftarrow {\theta }_d+\eta \nabla \tilde{V}({\theta }_d)$
    • 更新参数后，截断参数
• 从先验噪声分布$P_{prior(z)}$中再采样m个样本$\{z_1,z_2,\dots ,z_m\}$
• 更新生成器的参数θg，即最小化：
  • $\tilde{V}=\sout{\frac{1}{m}{\sum }_{i=1}^{m}logD(x_i)}-\frac{1}{m}{\sum }_{i=1}^{m}D(G(z_i))$
  • ${\theta }_g\leftarrow {\theta }_g-\eta \nabla \tilde{V}({\theta }_g)$

尤其需要注意的是, 判别器的输出不再需用sigmoid函数了! 并且需要训练k次判别器, 然后只训练一次生成器.

Gradient Penalty

WGA中试通过权重裁剪来施加1-Lipschitz限制的, 但是做样做会有一些问题, 比如通过权重裁剪并不能保证判别器满足1-Lipschitz限制, 而是K-Lipschitz限制, 而且权重裁剪很可能讲那些满足1-Lipschitz限制的函数给剪掉. 而WGAN GP提出了通过施加梯度惩罚来施加1-Lipschitz限制的条件.

Improved WGAN 的文章中提到, 1-Lipschitz函数有一个特性: 一个可微函数是1-Lipschitz函数时, 当且仅当它的梯度的norm将永远小于等于1, 即:
$$D\in 1-Lipschitz\iff ||\nabla xD(x)||\le 1forallx$$
有了这个理论, 我们就可以改变我们的目标函数了.
原来我们优化目标是:
$$W(P_{data},P_G)=\underset{D\in 1-Lipschitz}{\max }\{{\mathbb{E}}_{x\sim P_{data}}[D(x)]-{\mathbb{E}}_{x\sim P_G}[D(x)]\}$$
此时WGAN的优化目标是在1-Lipschitz中挑一个函数作为判别器D.
而Improved WGAN则是这样:
$$W(P_{data},P_G)=\underset{D}{\max }\{{\mathbb{E}}_{x\sim P_{data}}[D(x)]-{\mathbb{E}}_{x\sim P_G}[D(x)]-\lambda {\int }_{x}max(0,||\nabla xD(x)||-1)dx\}$$
也就是说, 现在我们寻找判别器的函数集不再是1-Lipschitz中的函数了, 而是任意函数. 但是后面增加了一项惩罚项. 这个惩罚项就能够让选中的判别器函数倾向于是一个“对输入梯度为1的函数”. 这样也能实现类似weight clipping的效果. 但与之前遇到的问题一样, 积分在实现的时候无法计算, 所以我们用采样的方法去计算这个惩罚项, 即:
$$W(P_{data},P_G)=\underset{D}{\max }\{{\mathbb{E}}_{x\sim P_{data}}[D(x)]-{\mathbb{E}}_{x\sim P_G}[D(x)]-\lambda {\mathbb{E}}_{x\sim P_{penalty}}[max(0,||\nabla xD(x)||-1)]\}$$
也就是说, 在训练过程中, 我们更倾向于得到一个判别器D, 它能对从$P_{p}enalty$中采样得到的每一个$x$都能$||\nabla xD(x)||\le 1$,. 涉及到采样, 那就要关系到如何采样. 而首先是从哪里采? 即$P_{p}enalty$是什么?
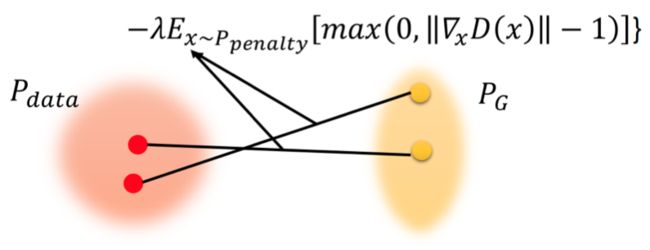
Improved WGAN设计了一个特别的$P_{p}enalty$. 它的产生过程如下:

1. 从Pdata中采样一个点
2. 从PG中采样一个点
3. 将这两个点连线
4. 在连线之上在采样得到一个点，就是一个从$P_{p}enalty$采样的一个点.

重复上面的过程就能不断采样得到$x\sim P_{penalty}$。最终得到下图中的蓝色区域就可以看作是$P_{penalty}$:

也就是说, 我们采样的范围不是整个$x$, 只是P_G和P_{data}中间的空间中的一部分.

再更进一步, Improved WGAN真正做的事是这样:
$$W(P_{data},P_G)=\underset{D}{\max }\{{\mathbb{E}}_{x\sim P_{data}}[D(x)]-{\mathbb{E}}_{x\sim P_G}[D(x)]-\lambda {\mathbb{E}}_{x\sim P_{penalty}}[(||\nabla xD(x)||-1{)}^2]\}$$
这个惩罚项的目的是让梯度尽可能趋向于等于1. 即当梯度大于1或小于1时都会受到惩罚. 而原来的惩罚项仅仅在梯度大于1时受到惩罚而已. 这样做是有好处的, 就像我们在SVM中强调最大类间距离一样, 虽然有多个可以将数据区分开的分类面, 但我们希望找到不但能区分数据, 还能让区分距离最大的那个分类面. 这里这样做的目的是由于可能存在多个判别器, 我们想要找到的那个判别器应该有一个“最好的形状”. 一个“好”的判别器应该在$P_{data}$附近是尽可能大, 要在$P_G$附近尽可能小. 也就是说处于$P_{data}$和$P_G$之间的$P_{penalty}$区域应该有一个比较“陡峭”的梯度. 但是这个陡峭程度是有限制的, 这个限制就是1.