论文学习 使用基于NeRF的精炼特征从3D感知Diffusion模型下实现单视点下的人工重建
论文学习 使用基于NeRF的精炼特征从3D感知Diffusion模型下实现单视点下的人工重建
- 论文连接
- 前言
- 摘要
- 介绍
- 相关工作
-
- 2.1 3D生成的扩散模型
- 2.2 单视点下的新视点生成
-
- 神经场(NeRF)以外的方法
- 基于神经场(NeRF)的方法
- 背景
-
- 3.1 图片条件NeRF
- 3.2 无几何视图合成
- NerfDiff
论文连接
NerfDiff: Single-image View Synthesis with NeRF-guided Distillation from 3D-aware Diffusion
前言
看到名字这么长是不是怕了??这其实只能说明我翻译能力太差了。很开心,这是加入我的导师实验室以来导师给我分配的第一篇论文,虽然我很菜,不过我也会努力达到老师的要求,以后我要在单视点下的CT三维重建方面发光发热,为导师做出点什么,也要为科学发展做出点什么。
摘要
这个领域非常重要,过去的工作做的不好,我们提出了一个模型NerfDiff,我们也同时改进了基于NeRF的提取算法来使得Conditional Diffusion model(CDM)能够生成连续的图。
介绍
过去有很多方法,近3年来,也有很多方法,他们有各自的缺点:
- NeRF,需要大量的图片,使其过拟合某一情景,导致其没有泛化能力,在未知情景下效果差
- 可泛化的NeRF,在目标视角距离相机视角较远时产生的结果是模糊的
- 通过使用2D生成模型来预测,只能产生部分3D连续的图片。
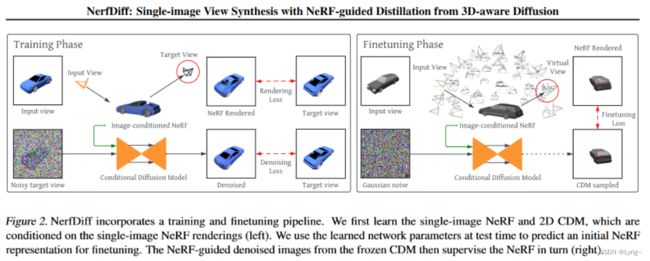
本文的提出了NerfDiff模型和“训练+微调”框架。
具体而言,在训练阶段,我们联合训练一个基于NeRF的相机三维场和构建在场景集合中的3D条件扩散模型。在微调阶段,我们初始化NeRF对给定图片的表示,之后我们继续利用CDM基于NeRF渲染的输出预测的图片来优化参数。我们发现朴素的优化策略是直接利用CDM的输出来优化NeRF的参数,然而这回导致低于目前标准的渲染结果,这是因为CDM的输出会导致多视角不连续。因此我们提出了NeRF指导的筛选,这更新了NeRF的表现同时以交互的方式指导了多视角的扩散过程。通过这种方式,单视角导致的不确定性可以通过CDM生成图片来补全未知信息,于此同时,NeRF也可以指导CDM使其能够做到具有多视角连续型扩散。
总而言之:
- 我们提出了全新的框架
- 引入了基于相机对齐三维场的有效条件NeRF表示
- 提出了3D CDM模型,将体绘制融入2D扩散模型,来提高其在新视角下的泛化性能。
相关工作
2.1 3D生成的扩散模型
之前的研究分为两类,一类是直接将扩散模型应用于3D场景,然而这样的问题在于,我们需要获取到Ground Truth才能进行,这在现实中很多情况下是很困难的。
另一类是先利用扩散模型生成2D场景,然后再从2D场景中学习到3D表示,这与我们的工作很像
这里埋下一个问题,利用2D生成3D是否也有不足?能否改进
2.2 单视点下的新视点生成
神经场(NeRF)以外的方法
最原始的方法是想实现一个单视点下的三维重建,这些方法通常通过一张图片和其真实情况作为训练数据,来映射其景深或者直接生成3D形状(感觉有点类似于计算机图形学的感觉)。另一些方法不需要Ground Truth来监督,然而这些方法只能重建几何形状,而不能重建其材质。近来的一些方法可以允许再不考虑多视角连续性的情况下实现生成,例如ENR方法利用卷积和投影将3D体素特征解码为RGB。SynSin模型期望解决更复杂环节下的生成,它利用了一个可微分的点云渲染器和一个图像绘制器来探索看不见的区域。InfiniteNature利用估计的深度来迭代的沿着某一相机轨迹绘制新的视角,其它的工作例如GeoFree和Pixelsynth使用前置的自回归来预测看不见的区域。最终,基于光场的方法条件Transformers将输入图片的特征映射到与输出色彩直接相关的查询光线,或者直接逆向到处隐空间。
基于神经场(NeRF)的方法
例如SinNeRF使用虚构的几何体来构建靠近输入视角的视角,最终,图片条件方法和VisionNeRF直接使用局部图像特征给condition NeRF,这与我们的方法很相关。需要注意的是,我们的方法也可以像pixelNeRF一样,再检验阶段不需要注释。
背景
3.1 图片条件NeRF
NeRF定义了一种隐式函数 f θ : ( x , d ) → ( c , σ ) f_{\theta}:(x, d) \rightarrow (c,\sigma) fθ:(x,d)→(c,σ),即给一个空间坐标 x ∈ R 3 x \in \R^{3} x∈R3和一条射线方向 d ∈ S 2 d \in S^{2} d∈S2,其中 θ \theta θ表示可学习的参数,其中 c a n d σ \bold{c}\quad and\quad \sigma candσ分别表示颜色和密度。渲染一张图片 I \bold{I} I,我们构造摄像机光线穿过每个像素 r ( t ) = x 0 + t d r(t)=x_0 + td r(t)=x0+td,其中 x 0 x_0 x0表示计算机原点,由此我们可以计算出该像素的颜色,通过对总量渲染进行积分来作为一种近似。
I θ ( r ) = ∫ t n t f ω ( t ) ⋅ c θ ( r ( t ) , d ) d t \bold{I}_{\theta}(r) = \int_{t_n}^{t_f}\omega(t)\cdot c_{\theta}(r(t), d)dt Iθ(r)=∫tntfω(t)⋅cθ(r(t),d)dt,其中 ω ( t ) = e − ∫ t n t σ θ ( r ( t ) , d ) d t \omega(t)=e^{-\int^{t}_{t_n}\sigma_{\theta}(r(t), d)dt} ω(t)=e−∫tntσθ(r(t),d)dt, t n t_n tn和 t f t_f tf表示光线最近和最远的边界。当多视点的图片是可以获取的, θ \theta θ可以很容易被优化,通过使用MSE Loss即可 L θ N e R F = E I ∼ d a t a , r ∼ R ( I ) ∥ I θ ( r ) − I ( r ) ∥ 2 2 \mathcal{L}_{\theta}^{NeRF}=E_{I\sim data, r \sim \mathcal{R}(I)}\|I_{\theta}(r) - I(r)\|^2_2 LθNeRF=EI∼data,r∼R(I)∥Iθ(r)−I(r)∥22为了捕捉高频细节,NeRF将x和d编码,编码方式是使用正弦位置函数 ξ p o s ( x ) , ξ p o s ( d ) \xi_{pos}(x),\xi_{pos}(d) ξpos(x),ξpos(d)
PixcelNeRF
给定一张输入图像 I s I^s Is,该模型首先提取出一个特征空间 W = e ψ ( I s ) W=e_{\psi}(I^s) W=eψ(Is),其中这个函数是可学习的图像编码器,因此对任何再输入相机空间中的3D点 x ∈ R 3 x\in \R^3 x∈R3,与之相关的特征可以先将x投影到图像平面 P ( x ) ∈ [ − 1 , 1 ] 2 \mathcal{P}(x)\in [-1,1]^2 P(x)∈[−1,1]2,这一步骤可以使用已知的矩阵,之后通过双线性插值来获得特征域 ξ W ( x ) = W ( P ( x ) ) \xi_W(x)=W(\mathcal{P}(x)) ξW(x)=W(P(x)),然后再将该特征与此前所说的颜色和密度特征组合,之后采用与NeRF一样的方法来进行,该方法中,对每一个场景,至少需要两个视角 L θ , ψ I C = E ( I s , I ) ∼ d a t a , r ∼ R ( I ) ∥ I θ , W ( r ) ( r ) − I ( r ) ∥ 2 2 \mathcal{L}_{\theta,\psi}^{IC}=\mathbb{E}_{(I^s,I)\sim data,r\sim \mathcal{R}(I)}\|I_{\theta, W(r)}(r)-I(r)\|_2^2 Lθ,ψIC=E(Is,I)∼data,r∼R(I)∥Iθ,W(r)(r)−I(r)∥22
以上方法存在挑战,即很难产生出高保真的渲染结果,尤其是图像出现严重遮挡的时候,这是因为单视点是一个未约束的问题,所以被遮挡的部分可能存在多种可能性,因此MSE Loss要求单张图片的NeRF从所有可能结果中回归到一种平均的像素值,从而产生模糊和不精确。
3.2 无几何视图合成
近来的条件扩散模型可以考虑进这种不确定性的挑战。用3DiM模型举例,它学习了一种条件噪音预测 ϵ ϕ \epsilon_{\phi} ϵϕ从而再给定输入视角的条件下,去噪那些经过高斯噪音处理的目标图片,从而获得新的视角。
而这一方法的问题就是会产生“对齐问题”——输入图片与目标视角间并非像素级别的对齐,从而当使用基于扩散模型的标准Unet网络时候产生劣质的泛化效果。使用交叉注意力机制能够减缓这种情况,但是需要大量算力,而且即使如此,在复杂情景下效果依然需要更多泛化能力。
