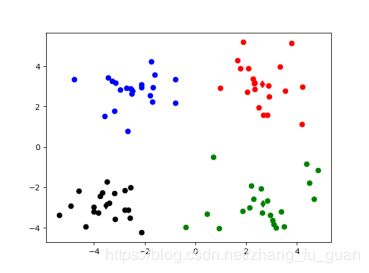
聚类-Kmeans+python3实现

 （主要是记录学习，让自己以后可以记忆）里面参考了别人的算法       

在聚类学习中，基本聚类算法我会采取划分方法（基于距离的算法，如K-means，K-medoids）和基于密度的方法（DBSCAN/OPTICS)和高级聚类——基于概率密度的聚类（GMM）。

1.划分方法：（1）发现球形互斥的簇（2）基于距离（3）可以用均值或中心点等代表簇中心 （4）对中小规模数据集有效

2.基于密度的方法：（1）可以发现任意形状的簇（2）簇是对象空间中被低密度区域分隔的稠密区域（3）簇密度：每个点的“邻域”内必须具有最少个数的点（4）可能过滤离群点。

在本章，重点介绍一下K-means。

1.简单介绍：

1.根据样本间的某种距离或者相似性来定义聚类，即把相似的（或距离近的）样本聚为同一类，而把不相似的（或距离远的）样本归在其他类。

2.  k-means算法是一种很常见的聚类算法，它的基本思想是：通过迭代寻找k个聚类的一种划分方案，使得用这k个聚类的均值来代表相应各类样本时所得的总体误差最小。          

k-means算法的基础是最小误差平方和准则。其代价函数是：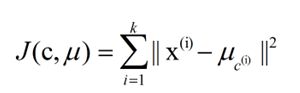

希望代价函数最小，直观的来说，各类内的样本越相似，其与该类均值间的误差平方越小，对所有类所得到的误差平方求和，即可验证分为k类时，各聚类是否是最优的。

2.算法

创建k个点作为初始的质心点（随机选择）

当任意一个点的簇分配结果发生改变时      

       对数据集中的每一个数据点              

             对每一个质心                  

                   计算质心与数据点的距离              

            将数据点分配到距离最近的簇      

       对每一个簇，计算簇中所有点的均值，并将均值作为质心      

       计算平均误差准则函数E      

       当连续两次聚类结果的平均误差准则函数小于0.0001时，迭代结束

3.算法实现

数据集：数据样本集我是从网上下载的，属于二维坐标点，一共有80组数据。选取了k=4

算法：参考了一位大佬博主的，但是忘记是哪位了，

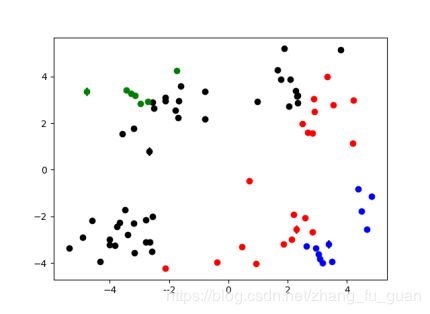
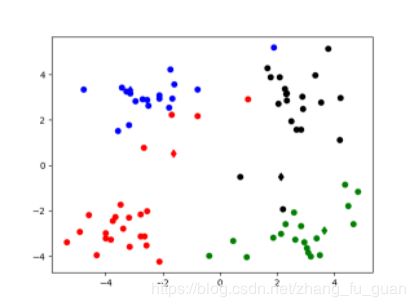
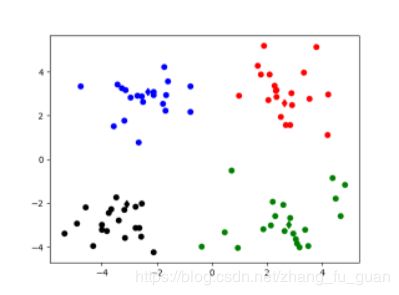
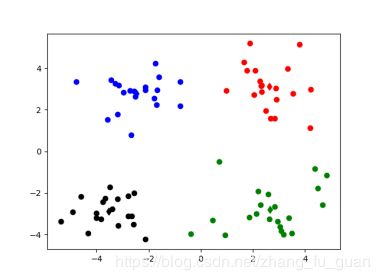
import numpy
import random
import codecs
import re
import matplotlib.pyplot as plt

'''1.加载数据'''
def loadDataSet(inputFile):
    #加载数据
    inData = codecs.open(inputFile,'r','utf-8').readlines()
    dataSet = list()
    for line in inData:
        line = line.strip()
        strList = re.split('[ ]+',line) #去掉多余的空格
        numList = list()
        for item in strList:
            num = float(item)
            numList.append(num)
        dataSet.append(numList)
    return dataSet
'''2.初始化k个质心'''
def initCentroids(dataSet,k):
    #随机获取
    return random.sample(dataSet,k) #从dataSet中随机获取k个数据项返回

'''3.计算两个点之间的距离'''
def calcuDistance(vec1,vec2):
    return numpy.sqrt(numpy.sum(numpy.square(vec1-vec2))) #欧几里得距离
    #return numpy.sum(numpy.abs(vec1-vec2))

'''4.对每个item，计算其与centroidList中k个质心的距离，找出距离最小的,然后将item放入相应簇中'''
def minDistance(dataSet,centroidList):
    cluster = {}#簇类结果用字典来保存
    for item in dataSet:
        vec1 = numpy.array(item) #转换成array形式
        flag = 0 #簇分类标记，记录与相应簇最近的那个簇
        minDis = float("inf") #初始化为最大值
        #寻找该点距离最小的那个质心
        for i in range(len(centroidList)):
            vec2 = numpy.array(centroidList[i])
            distance = calcuDistance(vec1,vec2)
            if distance < minDis:
                flag = i
                minDis = distance
        if flag not in cluster.keys():
            cluster[flag] = list()
        cluster[flag].append(item)
    return cluster

'''5.求均值获得新的质心/求中心点获得新的质心'''
def getCentroids(cluster):
    centroidList = []
    for key in cluster.keys():
        centroids = numpy.mean(numpy.array(cluster[key]),axis=0)
        centroidList.append(centroids)
    return numpy.array(centroidList).tolist()
'''6.计算簇集合间的均方误差'''
def getMSE(cluster,centroidList):
    #先计算每个点到所属质心的距离 求和 和方差
    #再求全部的MSE均方差
    sum = 0.0
    n = len(centroidList)
    for key in cluster.keys():
        vec1 = numpy.array(centroidList[key]) #该簇的质心
        distance = 0.0 #该簇的SSE
        for item in cluster[key]:
            vec2 = numpy.array(item)
            distance += numpy.sum(numpy.square(vec1-vec2))
        sum += distance
    MSE = sum
    return MSE

'''展示聚类结果'''
def showCluster(centroidList,cluster):
   colorMark =  ['or','ob','og','ok','oy','ow'] # 不同簇类的标记 'or' --> 'o'代表圆，'r'代表red，'b':blue
   centroidMark = ['dr','db','dg','dk','dy','dw'] #质心标记 d代表菱形
   for key in cluster.keys():
       plt.plot(centroidList[key][0],centroidList[key][1],centroidMark[key])#画质心
       for item in cluster[key]:
           plt.plot(item[0],item[1],colorMark[key]) #画该簇的其他点
   plt.show()


if __name__ == '__main__':
    fileName = "kmeans.txt"
    dataSet = loadDataSet(fileName)                         #获取数据集
    centroidList = initCentroids(dataSet,4)                 #初始化质心，设K为4
    clusterDic = minDistance(dataSet,centroidList)          #第一次聚类迭代
    newMSE = getMSE(clusterDic,centroidList)                #获得均方误差值，通过新旧均方误差获得迭代终止条件
    oldMSE = -0.0001
    print("*********第1次迭代*********")
    print("簇类")
    for key in clusterDic.keys():
        print(key,"-->",clusterDic[key])
    print("k个质心",centroidList)
    print("平均均方误差",newMSE)
    showCluster(centroidList,clusterDic) #展示第一次聚类结果
    k = 2
    while abs(newMSE - oldMSE) > 0.0001:#当连续两次聚类结果小于0.0001时，迭代结束
        centroidList = getCentroids(clusterDic) #获得新的质心
        clusterDic = minDistance(dataSet,centroidList) #新的聚类结果
        oldMSE = newMSE
        newMSE = getMSE(clusterDic,centroidList)

        print('*******第%d次迭代********'% k)
        print("簇类")
        for key in clusterDic.keys():
            print(key, "-->", clusterDic[key])
        print("k个质心", centroidList)
        print("平均均方误差", newMSE)
        showCluster(centroidList, clusterDic)  # 展示聚类结果
        k += 1

4.聚类结果

欧几里得距离(5次结束） 曼哈顿距离（11次结束）

迭代次数   平方误差 准则函数E	1	2	3	4	5	6	7	8	9	10	11
欧几里得距离（5次）	1018.6414	716.0856	176.7676	150.6260	150.6260
曼哈顿距离（11次）	622.9431	410.2834	401.6447	397.0213	384.4985	378.0871	321.1870	182.3721	152.2938	149.9543	149.9543

显然，使用欧几里得距离比曼哈顿距离迭代次数更少，但比较平均误差函数E来看，曼哈顿距离从一开始便小于欧几里得距离，最后趋于稳定时两者差不多。

经历5次迭代结束（欧几里得距离 部分截图）

5.kmeans优缺点

优点：

(1)是解决聚类问题的一种经典算法，简单、快速

(2)对处理大数据集，该算法保持可伸缩性和高效性

缺点：

(1)、在簇的平均值可被定义的情况下才能使用，可能不适用于某些应用；

(2)、在 K-means 算法中 K 是事先给定的，这个 K 值的选定是非常难以估计的。很多时候，事先并不知道给定的数据集应该分成多少个类别才最合适；

(3)、在 K-means 算法中，首先需要根据初始聚类中心来确定一个初始划分，然后对初始划分进行优化。这个初始聚类中心的选择对聚类结果有较大的影响，一旦初始值选择的不好，可能无法得到有效的聚类结果；

(4)、该算法需要不断地进行样本分类调整，不断地计算调整后的新的聚类中心，因此当数据量非常大时，算法的时间开销是非常大的；

(5)、若簇中含有异常点，将导致均值偏离严重（即:对噪声和孤立点数据敏感）；

(6)、不适用于发现非凸形状的簇或者大小差别很大的簇

 

该算法参考了某位博主，但是找不到是哪位了，我自己实现了一下，如果侵权了，对不起，找到那位博主后，会添上链接的.