基于深度学习的轴承故障识别-构建基础的LSTM模型
处理序列的基本深度学习算法分别是循环神经网络(recurrent neural network)和一维卷积神经网络(1D convnet)。长短时记忆网络(long short term memory network)作为循环神经网络的重要改型,克服了循环神经网络的诸多缺点,例如梯度消失问题,并逐渐替代经典循环神经网络。所以此处选择长短时记忆网络和一维卷积神经网络为备选模型,基于这两种神经网络模型构建轴承故障识别模型,并对比二者的识别效果。
LSTM
长短时记忆网络的循环单元结构的计算过程如下图所示,先利用上一时刻外部状态![]() 和当前时刻输入
和当前时刻输入![]() ,进行三个门的计算;然后结合遗忘门
,进行三个门的计算;然后结合遗忘门![]() 和输入门
和输入门![]() 更新记忆单元
更新记忆单元![]() ;最后结合输出门
;最后结合输出门![]() 将内部状态的信息同步给外部状态
将内部状态的信息同步给外部状态![]() 。
。
 LSTM循环单元结构(图来自邱锡鹏 神经网络与深度学习)
LSTM循环单元结构(图来自邱锡鹏 神经网络与深度学习)
长短时记忆网络顾名思义,包含了长时记忆和短时记忆,神经网络训练时的参数更新即为长时记忆,更新周期慢,积累了训练中的经验,短时记忆是循环神经网络中隐状态h存储的历史信息,因为每个时刻都会更新所以相对参数更新被称为短时记忆。
构建一个Sequential构造器,然后逐渐添加各网络层。先添加一个LSTM网络层,输出维度设为32,激活函数和用于循环时间步的激活函数都使用默认值,即激活函数为Tanh函数,用于循环时间步的函数为分段线性近似sigmoid函数。用于输入线性变换的权值矩阵的初始化器与用于循环层状态线性转换的权值矩阵初始化器也是用默认值,前者为glorot_uniform,以0为中心,标准差为![]() 的截断正态分布中抽取样本,其中
的截断正态分布中抽取样本,其中![]() 是权值张量中的输入单位的数量,
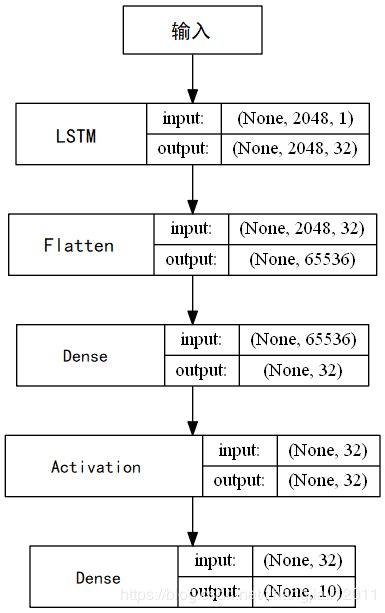
是权值张量中的输入单位的数量,![]() 是权值张量中的输出单位的数量;后者为orthogonal,能够随机生成一个正交矩阵。然后添加Flatten层展平,最后经过全连接层及softmax函数输出识别结果。神经网络模型的流程如下:
是权值张量中的输出单位的数量;后者为orthogonal,能够随机生成一个正交矩阵。然后添加Flatten层展平,最后经过全连接层及softmax函数输出识别结果。神经网络模型的流程如下:
LSTM模型训练结果如下:
| LSTM |
acc |
loss |
训练用时 |
备注 |
| 1 |
0.928 |
0.211338 |
15m47s |
|
| 2 |
0.856 |
0.575635 |
15m19s |
|
| 3 |
0.812 |
0.853626 |
15m26s |
|
| 4 |
0.881 |
0.255883 |
15m33s |
|
| 5 |
0.947 |
0.12195 |
15m29s |
|
| 6 |
0.799 |
1.858398 |
15m32s |
过拟合 |
| 7 |
0.941 |
0.124566 |
15m38s |
|
| 8 |
0.888 |
0.366132 |
15m20s |
|
| 9 |
0.828 |
1.776067 |
15m8s |
过拟合 |
| 10 |
0.979 |
0.075161 |
15m15s |
|
| 11 |
0.932 |
0.192733 |
15m13s |
|
| 12 |
0.839 |
1.818326 |
15m20s |
过拟合 |
| 13 |
0.816 |
1.522805 |
15m29s |
过拟合 |
| 14 |
0.838 |
0.619918 |
15m34s |
|
| 15 |
0.8 |
0.802467 |
15m10s |
|
| 16 |
0.913 |
0.301937 |
15m15s |
|
| 17 |
0.933 |
0.262946 |
15m16s |
|
| 18 |
0.859 |
1.761859 |
15m22s |
过拟合 |
| 19 |
0.886 |
0.433986 |
15m23s |
|
| 20 |
0.757 |
2.125751 |
15m23s |
过拟合 |
| 平均 |
0.8716 |
0.803074 |
15m24s |
|
由上表可以看出,基于LSTM的轴承故障检测模型可行,但有较多缺点。1)运行时间较长,训练一次用时均超过15分钟,效率较低,对设备要求较高;2)识别率较低,平均识别准确率仅有87.16%,不到90%,只有1次识别率超过95%;3)容易产生过拟合现象,在20次实验中就有6次发生过拟合。
附:
#coding:utf-8
"""
Created on Tue Apr 23 14:37:41 2019
@author: jiali zhang
bearing fault diagnosis by LSTM
"""
from keras.layers import Dense, Activation, Flatten, LSTM
from keras.models import Sequential
from keras.utils import plot_model
#from keras.regularizers import l2
import preprocess
from keras.callbacks import TensorBoard
import numpy as np
import time
# 训练参数
batch_size = 128
epochs = 12
num_classes = 10
length = 2048
BatchNorm = True # 是否批量归一化
number = 1000 # 每类样本的数量
normal = True # 是否标准化
rate = [0.7,0.2,0.1] # 测试集验证集划分比例
date=time.strftime("%Y%m%d", time.localtime())
mark=time.strftime("%Y%m%d_%H%M", time.localtime())
path = r'data\0HP'
x_train, y_train, x_valid, y_valid, x_test, y_test = preprocess.prepro(d_path=path,length=length,
number=number,
normal=normal,
rate=rate,
enc=True, enc_step=28)
x_train, x_valid, x_test = x_train[:,:,np.newaxis], x_valid[:,:,np.newaxis], x_test[:,:,np.newaxis]
input_shape =x_train.shape[1:]
print('训练样本维度:', x_train.shape)
print(x_train.shape[0], '训练样本个数')
print('验证样本的维度', x_valid.shape)
print(x_valid.shape[0], '验证样本个数')
print('测试样本的维度', x_test.shape)
print(x_test.shape[0], '测试样本个数')
model_name = "lstm_diagnosis-{}".format(mark)
# 实例化一个Sequential
model = Sequential()
model.add(LSTM(32, activation='tanh', recurrent_activation='hard_sigmoid', kernel_initializer='glorot_uniform', recurrent_initializer='orthogonal', bias_initializer='zeros', return_sequences=True))
model.add(Flatten())
# 增加输出层,共num_classes个单元,激活函数为softmax
#model.add(Dense(units=num_classes, activation='softmax', kernel_regularizer=l2(1e-4)))
model.add(Dense(units=num_classes, activation='softmax'))
# 编译模型 评价函数和损失函数相似,不过评价函数的结果不会用于训练过程中
model.compile(optimizer='Adam', loss='categorical_crossentropy',
metrics=['accuracy'])
# TensorBoard调用查看一下训练情况
tb_cb = TensorBoard(log_dir='logs/{}_logs/{}'.format(date, model_name))
# 开始模型训练
model.fit(x=x_train, y=y_train, batch_size=batch_size, epochs=epochs,
verbose=1, validation_data=(x_valid, y_valid), shuffle=True,
callbacks=[tb_cb])
# 评估模型
score = model.evaluate(x=x_test, y=y_test, verbose=0)
print("测试集上的损失率:", score[0])
print("测试集上的准确率:", score[1])
plot_model(model=model, to_file='images/lstm-diagnosis.png', show_shapes=True)
点击此处返回总目录:基于深度学习的轴承故障识别