机器学习（回归九）——SoftMax回归-代码实现

上篇博客说的是SoftMax回归的基本内容，包括公式推导。这篇博客基于葡萄酒数据进行葡萄酒质量预测模型构建，使用Softmax算法构建模型，并获取Softmax算法构建的模型效果(注意：分成11类)

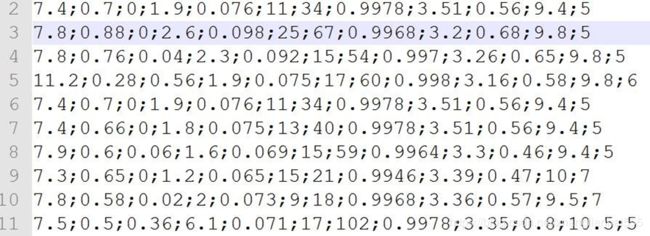
数据

数据来源：Wine Quality Data Set

数据概要：

数据的属性

翻译过来，大致内容：

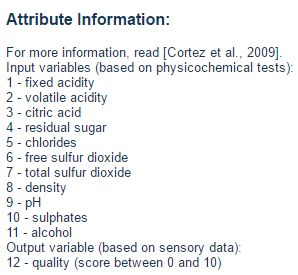
属性信息:
输入变量(基于理化测试):
1 -固定酸度
2 -挥发性酸度
3 -柠檬酸
4 -残余糖
5 -氯化物
6 -游离二氧化硫
7 -二氧化硫总量
8 -密度
9 - pH值
10 -硫酸盐
11 -酒精
输出变量(基于感官数据):
12 -质量(0 - 10分)

看几条具体数据

代码

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import pandas as pd
import warnings
import sklearn
from sklearn.linear_model import LogisticRegressionCV
from sklearn.linear_model.coordinate_descent import ConvergenceWarning
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import label_binarize
from sklearn import metrics

## 设置字符集，防止中文乱码
mpl.rcParams['font.sans-serif']=[u'simHei']
mpl.rcParams['axes.unicode_minus']=False
## 拦截异常
warnings.filterwarnings(action = 'ignore', category=ConvergenceWarning)

## 读取数据
path1 = "datas/winequality-red.csv"
df1 = pd.read_csv(path1, sep=";")
df1['type'] = 1 # 设置数据类型为红葡萄酒

path2 = "datas/winequality-white.csv"
df2 = pd.read_csv(path2, sep=";")
df2['type'] = 2 # 设置数据类型为白葡萄酒

# 合并两个df
df = pd.concat([df1,df2], axis=0)

## 自变量名称
names = ["fixed acidity","volatile acidity","citric acid",
         "residual sugar","chlorides","free sulfur dioxide",
         "total sulfur dioxide","density","pH","sulphates",
         "alcohol", "type"]
## 因变量名称
quality = "quality"

## 显示
df.head(5)

## 异常数据处理
new_df = df.replace('?', np.nan)
datas = new_df.dropna(how = 'any') # 只要有列为空，就进行删除操作
print ("原始数据条数:%d；异常数据处理后数据条数:%d；异常数据条数:%d" % (len(df), len(datas), len(df) - len(datas)))

原始数据条数:6497；异常数据处理后数据条数:6497；异常数据条数:0

## 提取自变量和因变量
X = datas[names]
Y = datas[quality]

## 数据分割
X_train,X_test,Y_train,Y_test = train_test_split(X,Y,test_size=0.25,random_state=0)

print ("训练数据条数:%d；数据特征个数:%d；测试数据条数:%d" % (X_train.shape[0], X_train.shape[1], X_test.shape[0]))

训练数据条数:4872；数据特征个数:12；测试数据条数:1625

# 2. 数据格式化(归一化)
# 将数据缩放到[0,1]
ss = MinMaxScaler()
X_train = ss.fit_transform(X_train) ## 训练模型及归一化数据

## 查看y值的范围和数理
Y_train.value_counts()

5 1606
7 805
4 161
8 146
3 20
9 2
Name: quality, dtype: int64

# 3. 模型构建及训练
## penalty: 过拟合解决参数,l1或者l2

## solver: 参数优化方式
### 当penalty为l1的时候，参数只能是：liblinear(坐标轴下降法)；
### 当penalty为l2的时候，参数可以是：lbfgs(拟牛顿法)、newton-cg(牛顿法变种)

## multi_class: 分类方式参数；参数可选: ovr(默认)、multinomial；这两种方式在二元分类问题中，效果是一样的；在多元分类问题中，效果不一样
### ovr: one-vs-rest， 对于多元分类的问题，先将其看做二元分类，分类完成后，再迭代对其中一类继续进行二元分类
### multinomial: many-vs-many（MVM）,对于多元分类问题，如果模型有T类，我们每次在所有的T类样本里面选择两类样本出来，
#### 不妨记为T1类和T2类，把所有的输出为T1和T2的样本放在一起，把T1作为正例，T2作为负例，
#### 进行二元逻辑回归，得到模型参数。我们一共需要T(T-1)/2次分类

## class_weight: 特征权重参数

### Softmax算法相对于Logistic算法来讲，在sklearn中体现的代码形式来讲，主要只是参数的不同而已
## Logistic算法回归(二分类): 使用的是ovr；如果是softmax回归，建议使用multinomial
lr = LogisticRegressionCV(fit_intercept=True, Cs=np.logspace(-5, 1, 100), 
                          multi_class='multinomial', penalty='l2', solver='lbfgs')
lr.fit(X_train, Y_train)

# 4. 模型效果获取
r = lr.score(X_train, Y_train)
print("R值：", r)
print("特征稀疏化比率：%.2f%%" % (np.mean(lr.coef_.ravel() == 0) * 100))
print("参数：",lr.coef_)
print("截距：",lr.intercept_)
print("概率：", lr.predict_proba(X_test)) # 获取sigmoid函数返回的概率值
print("概率：", lr.predict_proba(X_test).shape) # 获取sigmoid函数返回的概率值

R值： 0.5496715927750411
特征稀疏化比率：0.00%
参数： [[ 0.9730127 2.16084285 -0.41754754 -0.49107226 0.90062986 1.4392444
0.75285349 0.23015819 0.00696097 -0.69411951 -0.71662184 -0.29344398]
[ 0.62645663 5.12629124 -0.38350372 -2.1611902 1.21085251 -3.71460614
-1.45924414 1.33501236 0.33882333 -0.86777815 -2.74856763 2.03150322]
[-1.73734378 1.95681945 0.48966012 -1.91168338 0.64512953 -1.67662964
2.20493483 1.49022497 -1.3581056 -2.23627334 -5.01448694 -0.75503315]
[-1.19653545 -2.61094004 -0.34375325 0.17322861 -0.04192244 0.8170301
-0.28178849 0.51768511 -0.67621769 0.185218 0.01886649 -0.71342696]
[ 1.15776936 -4.66419 -0.30888948 2.21347594 -2.00208967 1.66891233
-1.02875476 -2.14504321 0.80606712 2.68429533 3.36550273 -0.73559995]
[-0.07708272 -1.8260927 0.69470163 2.0761507 -0.6231927 1.49048446
-0.15842754 -1.36420613 0.72475406 1.06822926 4.69108042 0.04776849]
[ 0.25372326 -0.1427308 0.26933225 0.10109059 -0.08940709 -0.02443551
-0.02957338 -0.06383129 0.15771782 -0.13957159 0.40422677 0.41823233]]
截距： [-2.33409277 -1.16759486 4.90906789 4.31851264 1.29806235 -2.26232821
-4.76162703]
概率： [[2.29894328e-03 3.30729714e-02 4.66552531e-01 … 5.29492016e-02
5.83107037e-03 3.08278584e-04]
[2.39084537e-03 1.73052873e-02 8.05569443e-02 … 3.13136934e-01
3.58259317e-02 4.63436966e-04]
[3.37404394e-03 1.55263335e-02 3.98405130e-01 … 8.76639384e-02
1.21057934e-02 3.78833283e-04]
…
[3.27231592e-03 1.62465297e-02 8.38101430e-02 … 3.70830765e-01
5.46102363e-02 5.42625050e-04]
[4.98416654e-03 2.55531822e-02 7.29802986e-01 … 1.82922910e-02
2.68720817e-03 1.48008504e-04]
[5.89788267e-03 3.64331319e-02 3.99745247e-01 … 8.04591823e-02
1.82397973e-02 5.04254984e-04]]
概率： (1625, 7)

# 数据预测
## a. 预测数据格式化(归一化)
X_test = ss.transform(X_test) # 使用模型进行归一化操作

## b. 结果数据预测
Y_predict = lr.predict(X_test)

## c. 图表展示
x_len = range(len(X_test))
plt.figure(figsize=(14,7), facecolor='w')
plt.ylim(-1,11)
plt.plot(x_len, Y_test, 'ro',markersize = 8, zorder=3, label=u'真实值')
plt.plot(x_len, Y_predict, 'go', markersize = 12, zorder=2, label=u'预测值,$R^2$=%.3f' % lr.score(X_train, Y_train))
plt.legend(loc = 'upper left')
plt.xlabel(u'数据编号', fontsize=18)
plt.ylabel(u'葡萄酒质量', fontsize=18)
plt.title(u'葡萄酒质量预测统计', fontsize=20)
plt.show()

看一下效果：

红色的点 ∙ $\bullet$∙ 表示的真实值，绿色的点 ∙ $\bullet$ 是我们预测的值，最终结果似乎不太好哈。