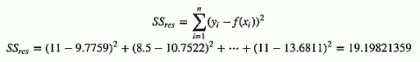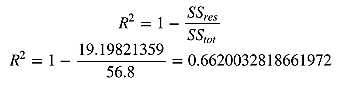python一元线性回归

上图中，'x'轴表示匹萨直径，'y'轴表示匹萨价格。 能够看出，匹萨价格与其直径正相关，这与我们的日常经验也比较吻合，自然是越大越贵。 下面就用 scikit-learn 来构建模

#!/usr/bin/env python
# -*- coding:utf-8 -*-
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
font = FontProperties(fname=r"C:\Windows\Fonts\myinghwl.ttf") 
from sklearn.linear_model import LinearRegression #创建拟合模型#
def runplt():
    plt.figure()
    plt.title('LINE1', fontproperties=font)
    plt.xlabel('LINE', fontproperties=font)
    plt.ylabel('PRICES', fontproperties=font)
    plt.axis([0, 25, 0, 25])
    plt.grid(True)
    return plt
plt = runplt()
X = [[6], [8], [10], [14], [18]]
y= [[7], [9], [13], [17.5], [18]]
plt.plot(X,y,'.k')
plt.show()
model = LinearRegression()
model.fit(X,y)
print('12prices:$%.2f'% model.predict(12))

PS.想通过fontproperties将文字在图像中显示出来，结果 gg了 ，还不知道问题出在哪里....只能把中文名随便改了个英文名

一元线性回归假设解释变量和响应变量之间存在线性关系、、这个线性模型所构成的空间是一个超平面（hyperplane）。 超平面是 n 维欧氏空间中余维度、于一的线性子空间，如平面中的直线、空间中的平面、，总比包含它的空间少一维。 在一元线性回归中，一个维度是响应变量，另一个维度是解释变量，总共两维。 因此，其超平面只有一维，就是一条线

上述代码中 sklearn.linear_model.LinearRegression 类是一个估计器（estimator）。 估计 器依据观测值来预测结果。 在 scikit-learn 里面，所有的估计器都带有 fit() 和 predict() 方法。

 fit() 用来分析模型参数，predict() 是通过 fit() 算出的模型参数构成的模型，对解释变量进行预测获得的值。 

因为所有的估计器都有这两种方法，所有 scikit-learn 很容易实验不同的模型。 LinearRegression 类的 fit() 方法学习下面的一元线性回归模型： Y=A+BX

y 表示响应变量的预测值，本例指匹萨价格预测值， 是解释变量，本例指匹萨直径。 截距和相关系数 是线性回归模型最关心的事情. 。 用这个模型，可以计算不同直径的价格，8 英寸 $7.33，20 英寸 $18.75

一元线性回归拟合模型的参数估计常用方法是普通最小二乘法（ordinary least squares ）或线性最小二乘法（linear least squares）。 首先，我们定义出拟合成本函数，然后对参数进行数理统计。

成本函数（cost function）也叫损失函数（loss function），用来定义模型与观测值的误差。 模型预测的价格与训练集数据的差异称为残差（residuals）或训练误差（training errors）。 后面会用模型计算测试集，那时模型预测的价格与测试集数据的差异称为预测误差（prediction errors）或训练误差（test errors）

模型的残差是训练样本点与线性回归模型的纵向距离，如下图所示：

X2=[[0],[10],[14],[25]]
model = LinearRegression()
model.fit(X,y)
y2=model.predict(X2)
plt.plot(X,y,'.k')
plt.plot(X2,y2,'.g')#残差值预测#
yr= model.predict(X)
for idx,x in enumerate(X):
    plt.plot([x, x], [y[idx], yr[idx]], 'r-')
plt.show()

我们可以通过残差之和最小化实现最佳拟合，也就是说模型预测的值与训练集的数据最接近就是最佳拟合。 对模型的拟合度进行评估的函数称为残差平方和（residual sum of squares）成本函数。 就是让所有训练数据与模型的残差的平方之和最小化，如下所示：

import numpy as np
print('square:%.2f'% np.mean((model.predict(X)-y)**2))
#我们可以通过残差之和最小化实现最佳拟合，也就是说模型预测的值与训练集的数据最接近就是最佳拟合。 对模型的拟合度进行评估的函数称为残差平方和（residual sum of squares）成本函数。

解一元线性回归的最小二乘法

通过成本函数最小化获得参数，先求相关系数贝塔。 按照频率论的观点，首先需要计算 x 的方差和 x 与 y 的协方差

方差是用来衡量样本分散程度的。 如果样本全部相、、，那么方差为 0。 方差越小，表示样本越集中，反正则样本越分散。 方差计算公式如下：

xbar = (6+8+10+14+18)/5
variance = ((6-xbar)**2+(-xbar)**2+(0-xbar)**2+(14-xbar)**2+(18-xbar)**2)/4
print (variance)
#通过成本函数最小化获得参数，先求相关系数贝塔。 按照频率论的观点，首先需要计算 x 的方差和 x 与 y 的协方差
#方差是用来衡量样本分散程度的。 如果样本全部相、、，那么方差为 0。 方差越小，表示样本越集中，反正则样本越分散。 方差计算公式如下：
print(np.var([6,8,10,14,18],ddof=1))#Numpy 里面有 var 方法可以直接计算方差，ddof 参数是贝塞尔 (无偏估计) 校正系数（Bessel'scorrection），设置为 1，可得样本方差无偏估计量

协方差表示两个变量的总体的变化趋势。 如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。 如果两个变量不相关，则协方差为 0，变量线性无关不表示一定没有其他相关
性。 协方差公式如下：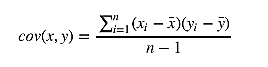

ybar =(7+9+13+17.5+18)/5
cov=((6-xbar)*(7-ybar)+(8-xbar)*(9-ybar)+(10-xbar)*(13-ybar)+(14-xbar)*(17.5-ybar)+(18-xbar)*(18-ybar))/4
print (cov)

现在有了方差和协方差，就可以计算相关系统贝塔了

算出贝塔后，就可以计算阿尔法了：

将前面的数据带入公式就可以求出阿尔法了：

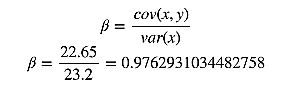
α = 12.9 − 0.9762931034482758 × 11.2 = 1.9655172413793114
这样就通过最小化成本函数求出模型参数了。 把匹萨直径带入方程就可以求出对应的价格了，如 11 英寸直径价格 $12.70，18 英寸直径价格 $19.54

有些度量方法可以用来评估预测效果，我们用 R 方（r-squared）评估匹萨价格预测的效果。 R 方也叫确定系数（coefficient of determination），表示模型对现实数据拟合的程度。 计算 R 方的方法有几种。 一元线性回归中 R 方、、于皮尔逊积矩相关系数（Pearson product moment correlation coefficient 或 Pearson's r）的平方
这种方法计算的 R 方一定介于 0～1 之间的正数。 其他计算方法，包括 scikit-learn 中的方法，不是用皮尔逊积矩相关系数的平方计算的，因此当模型拟合效果很差的时候 R 方会是负值。 下面用 scikitlearn 方法来计算 R 方

=56.8
然后，计算残差平方和，和前面的一样：

R 方是 0.6620 说明测试集里面过半数的价格都可以通过模型解释。 现在，用 scikit-learn 来验证一下。 LinearRegression 的 score 方法可以计算 R 方：

#测试集
X_test = [[8],[9],[11],[16],[12]]
y_test = [[11],[8.5],[15],[18],[11]]
model = LinearRegression()
model.fit(X,y)
model.score(X_test,y_test)
print (model.score(X_test,y_test))

参考地址 https://www.jianshu.com/p/738f6092ef53