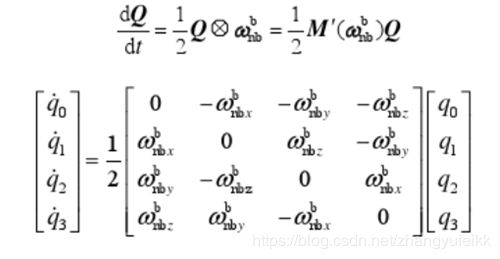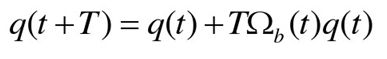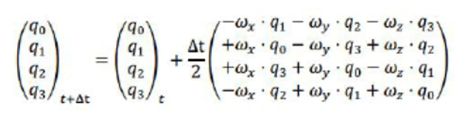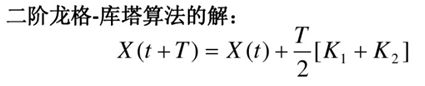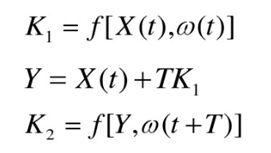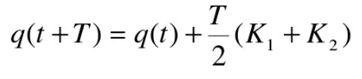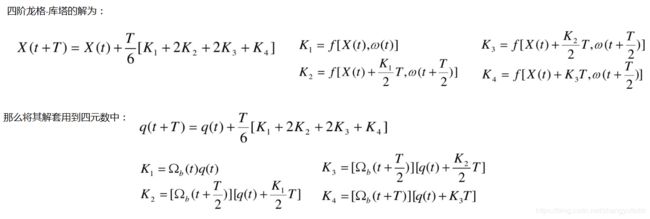从原理到代码 梳理姿态更新计算的四元数算法

前言

    姿态解算过程涉及到两个坐标系，一个是运载体的机体坐标系，该坐标系与运载体固连，当运载体转动的时候，这个坐标系也跟着转动，我们假设运载体的坐标系为b系。另外一个是地理坐标系，即东北天坐标系，X轴指向东，Y轴指向北，Z轴指向天，这个坐标系也称为导航坐标系，我们假设这个坐标系为n系。   

 所谓的姿态解算，就是求出当前的机体坐标系b相对于地理坐标系n的变化。由于n系和b 系均为直角坐标系，各轴之间始终保持直角，所以可将坐标系理解成刚体，当只研究两个坐标系间的角位置关系时，可理解成刚体的定点转动。而刚体定点转动这个变化可以通过一个变换矩阵来表示，这个矩阵包含了刚体的所有姿态信息。

可以这么理解这个变换矩阵：对于机体坐标系中的一个向量，当它左乘这个变换矩阵之后，就能得出这个向量在地理坐标系中的大小。 由b系到n系的坐标变换短阵也称为运载体的姿态矩阵，而我们姿态解算的目标就是根据惯性器件的输出实时计算出这个姿态矩阵，从而实时获取当前的偏航、俯仰角、翻滚角。

陀螺仪和加速度计分别用来测量运载体的角运动信息和线运动信息，根据陀螺仪和加速度计的输出，我们就能实时跟新这个姿态矩阵。

本篇文档将从这一基本思想出发，主要介绍姿态更新的四元数算法。

变换矩阵的三种表示方法：欧拉角，余弦矩阵，四元数

1、欧拉角：欧拉角是很直观的，一个物体的旋转，可以分解到三个坐标轴上的旋转。这三个旋转角度就是欧拉角。在惯性系统中一般把这三个角度分别称为roll，pitch，yaw。用欧拉角来描述物体的旋转不光需要有角度，还需要有旋转顺序，一般旋转顺序是先yaw后pitch，再roll反应到坐标轴上就是先绕Z轴旋转，再绕X轴旋转，最后绕Y轴旋转。需要注意的是 yaw pitch roll 都是对应的固定的参考系（地理坐标系），每次新的姿态坐标系都是由地理坐标系通过欧拉角旋转得到的。这样我们就用欧拉角表示了物体的姿态。如右下图我们就得到了使用欧拉角表示的坐标变换矩阵。

2、余弦矩阵：方向余弦表示一个向量的方向（姿态）我们可以用他在参考坐标系（地理坐标系）各个轴向的夹角的余弦来表示（及在各个轴的投影）。类似的 一个坐标系 可以看成是3个向量组成，所以三个向量分别在坐标轴上的投影可以用来表示一个坐标系与参考坐标系的关系。这总共9个方向余弦组成了一个三阶矩阵。在本体坐标系下的 i, j, k在全局坐标系(I,J,K)下有一套完整的表示，我们可以将这些向量组成一个方便的矩阵，其中cos(I,i) = |I||i| cos(I,i) = I.i，即|i|为单位向量i的范数(长度)，cos(I,i)为向量I与i形成的夹角余弦：

事实上 方向余弦和欧拉角没有本质区别，因为方向余弦实际上就是用欧拉角表示的。这里就不再赘述了。

3、四元数：欧拉角微分方程中包含了大量的三角运算，这给实时解算带来了一定的困难。而且当俯仰角为90度时方程式会出现神奇的“GimbalLock”。四元数法只求解四个未知量的线性微分方程组，计算量小，易于操作，是比较实用的工程方法。因此姿态更新更多的使用的是四元数更新算法。

思维导图

四元数简介

（摘自《惯性导航》秦永元著）

四元数与姿态矩阵间的关系

（摘自《惯性导航》秦永元著）

四元数微分方程

（摘自《惯性导航》秦永元著）

四元数微分方程

这样我们就可以得到四元数Q关于角速度向量的实时更新的微分方程

从理论上来看，角速度信息由陀螺仪提供，因此我们只需要获得角速度信息就可以进行联捷惯导的计算。

但是在实际中，我们还需要考虑到，陀螺仪自身的动静态误差的补偿，以及来自地球的位置速率和自转速率的影响。

所以在实际应用中，也需要加速度计和磁力计来对这些误差进行补偿。

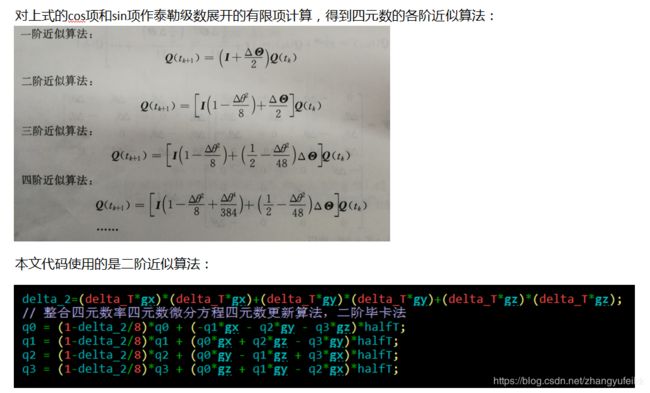
四元数微分方程求解法

毕卡求解法：

捷联陀螺的输出一般是采样时间间隔内的角增量，为了避免噪声的微分放大，应直接用角增量来确定四元数。毕卡算法就是由角增量计算四元数的常用算法。

上一节介绍了四元数的微分方程，如下：

龙格-库塔法（Runge-Kutta）

对于泰勒级数而言，虽然高精度，但是计算复杂，而龙格-库塔法则能大大改善泰勒公式的这一缺陷。

这是一种在工程上应用广泛的高精度单步算法。由于此算法精度高，采取措施对误差进行抑制，所以其实现原理也较复杂。该算法是构建在数学支持的基础之上的。
假设有一个矩阵微分方程为：

当初是条件已知，那么它的一阶解为：

那么套用到四元数中，可有：                                                                                                  

展开得：

将其写成代码为：

一阶龙格-库塔法是用初始端点的斜率来近似T时间段内的斜率，而二阶龙格-库塔法是使用初始端点和末尾端点的平均斜率来近似T时间段内的斜率。

则

其中

那么将其解套用到四元数中：                                                                                          

其中

当然，经典的龙格-库塔方法是四阶的。也就是在[xi,xi+1][xi,xi+1]上用四个点处的斜率加权平均作为平均斜率k∗的近似值，构成一系列四阶龙格-库塔公式。

代码实现

这部分可以看一下我的上一篇博客《基于icm20609姿态更新计算的四元数算法》

https://blog.csdn.net/zhangyufeikk/article/details/94391858

 

 

本文感谢以下大佬的贴子，获益匪浅：

https://wenku.baidu.com/view/218c876d856a561253d36f2a.html

https://wenku.baidu.com/view/b2f5ac27a5e9856a561260ce.html