MATLAB 粒子群算法,例题与常用模版
本文学习自:Particle Swarm Optimization in MATLAB - Yarpiz Video Tutorial 与《精通MATLAB智能算法》
1. 简介:
Particle Swarm Optimization ,粒子群优化算法,常用来找到方程的最优解。
2. 算法概述:
每次搜寻都会根据自身经验(自身历史搜寻的最优地点)和种群交流(种群历史搜寻的最优地点)调整自身搜寻方向和速度。
3. 算法优势:
- 相较于传统算法计算速度非常快,全局搜索能力也很强;
- PSO对于种群大小不十分敏感,所以初始种群往往设为500-1000,不同初值速度影响也不大;
- 粒子群算法适用于连续函数极值问题,对于非线性、多峰问题均有较强的全局搜索能力。
4. 算法基本原理
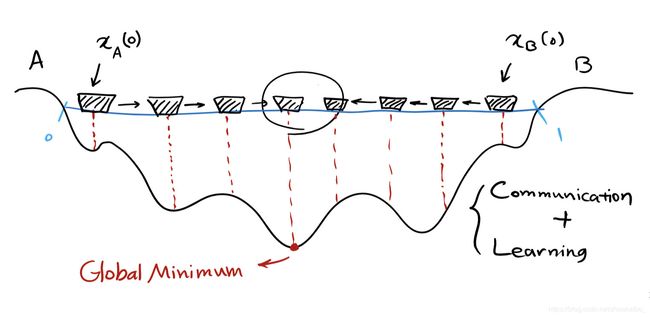
一个形象的例子:
A与B两个小粒子初始时在河的两侧,他们想要找到河最深处。如果A某时刻所在位置的深度比B的浅,A就会像B的方向走,反之亦然。 当A到达Global Minimum(全局最小值)时,B会一直向着A前进,直到在optimum solution(全剧最优解)处汇合。
4.1 概述
从上面的示例中我们得到两个准则,也可以说是每个粒子的必要特性:
Communication: 彼此互相通知Learning: 不停地学习以达最优解
数量众多的粒子通过相互的交流与学习,全部粒子最终将汇聚到一点,即问题的解。粒子间相互交流与学习的过程用数学或计算机语言描述为迭代。
迭代的意义在于不断寻找更优的值,从理论上来说,如果我们掌握了一种可以不停寻找到更优解答的方法,通过不停的迭代,我们就能够找到最优的答案。
Learning the concept of better is the main problem that an optimizer should solve. Then an optimizer learns the concept of better, it is able to solve any kind of optimuzation.Because the solution of optimization problem is to find the best one . So if we know what is the better, we actually can discover the concept of best.
4.2 粒子的基本信息
回顾粒子群算法概述:
每次搜寻都会根据自身经验(自身历史搜寻的最优地点)和种群交流(种群历史搜寻的最优地点)调整自身搜寻方向和速度。
我们首先聚焦与粒子本身,或许全部粒子研究起来很复杂,但单个粒子的属性是很简单的。
首先,每个粒子包含两个基本信息,Position(位置) & Velocity(速度)。
在粒子群算法的每次迭代中,每个粒子的位置和速度都会更新。
4.3 粒子的个体极值与全局极值
回顾粒子群算法概述:
每次搜寻都会根据自身经验(自身历史搜寻的最优地点)和种群交流(种群历史搜寻的最优地点)调整自身搜寻方向和速度。
仅有上述位置与速度两个信息还不够,我们之前提到过,每一个粒子是会学习的。 每个粒子还拥有下面两个信息(每个信息都是一个向量):
-
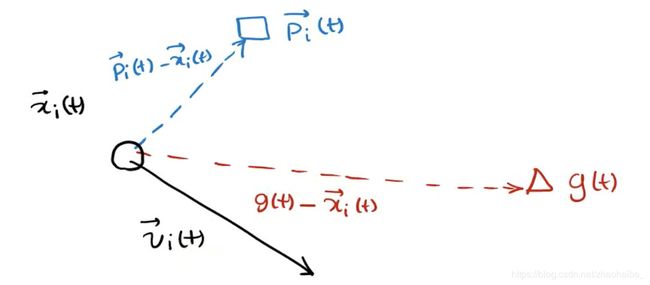
每一个粒子有它自己的记忆,会记住自己的best position , best experience,即个体极值 (personal best), 标记为 P i ( t ) ⃗ \vec { P_i (t)} Pi(t)
-
当前时刻全局的最优解,即全局极值(Common best experience among the members),标记为 g i ( t ) ⃗ \vec { g_i (t)} gi(t)
总结:PSO初始化为一群随机粒子,然后通过迭代找到最优解。在每一次迭代过程中,粒子通过跟踪两个极值来更新自己,一个是粒子本身所找到的最优解,这个解称为个体极值 P i ( t ) ⃗ \vec { P_i (t)} Pi(t);另一个极值是整个种群目前找到的最优解,这个极值是全局极值 g i ( t ) ⃗ \vec { g_i (t)} gi(t) 。
4.4 找到新位置
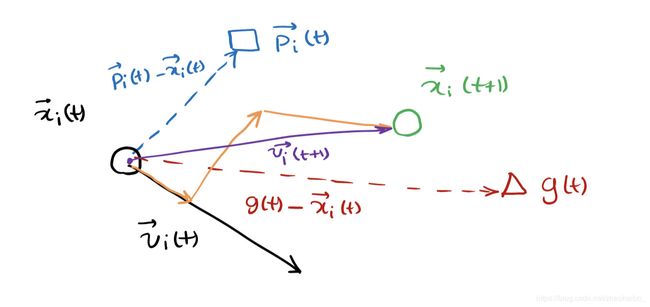
根据平行四边形法则,已知个体极值与整体极值,有了新时刻的速度 V i ⃗ ( t + 1 ) \vec {V_i}(t+1) Vi(t+1) ,会得到新的位置 X i ⃗ ( t + 1 ) \vec {X_i}(t+1) Xi(t+1)
状态转移方程:
v i j ⃗ ( t + 1 ) = w v i j ⃗ ( t ) + c 1 r 1 ( p i j ( t ) − x i j ⃗ ( t ) ) + c 2 r 2 ( g j ( t ) − x i j ⃗ ( t ) ) (4-1) \vec {v_{ij}}(t+1) = w\vec{v_{i j}} (t) + c_1r_1(p_{ij} (t) - \vec{x_{ij}}(t))+c_2r_2(g_j(t)-\vec{x_{ij}}(t)) \tag{4-1} vij(t+1)=wvij(t)+c1r1(pij(t)−xij(t))+c2r2(gj(t)−xij(t))(4-1)
x i j ⃗ ( t + 1 ) = x i j ⃗ ( t ) + v i j ⃗ ( t + 1 ) (4-2) \vec {x_{ij}}(t+1) = \vec{x_{ij}}(t)+\vec{v_{ij}}(t+1) \tag{4-2} xij(t+1)=xij(t)+vij(t+1)(4-2)
其中, c 1 , c 2 c_1,c_2 c1,c2为学习因子,也称加速常数(acceleration constant);
r 1 , r 2 r_1,r_2 r1,r2,[0,1]范围内的均匀随机数。
式(1)右边由三部分组成:
- 第一部分为“惯性(inertia)”或“动量(MOMENTUM)”部分,反映了粒子的运动习惯,代表粒子有维持自己先前速度的趋势。
- 第二部分为“认知(cognition)”部分,反映了粒子对自身历史经验的记忆,代表粒子由向自身历史最佳位置逼近的趋势。
- 第三部分为“社会(social)”部分,反映了粒子间协同合作与知识共享的群体历史经验,代表粒子有向群体或领域历史最佳位置逼近的趋势。
5. 算法的运行参数
PSO算法一个最大的优点是不需要调节太多的参数,但是算法中少数几个参数却直接影响着算法的性能和收敛性。
基本粒子群算法有下述7个运行参数需要提前设定:
- r r r:粒子群算法的种子数,对粒子群算法中种子数值可以随机生成也可以固定位一个初始的数值,要求能涵盖目标函数的范围内。
- m m m:粒子群群体大小,即群体中所含个体的数量,一般取为20~40。在变两年比较多的时候可以取100以上较大的数。
- m a x d max_d maxd:一般为最大迭代次数以最小误差的要求满足的。粒子群算法的最大迭代次数,也是终止条件数。
- r 1 , r 2 r_1,r_2 r1,r2:两个在[0,1]之间变化的加速度权重系数随机产生。
- c 1 , c 2 c_1,c_2 c1,c2:加速常数,取随机2左右的值。
- w w w:惯性权重产生的。
- v k , x k v_k,x_k vk,xk:一个粒子的速度和位移数值,用粒子群算法迭代出每一组的数值。
6. 算法的基本流程
- 初始化粒子群,包括群体规模N,每个粒子的位置 x i x_i xi和速度 v i v_i vi。
- 计算吗每一个粒子的适应度值 F i t [ i ] Fit[i] Fit[i]。
- 计算每个粒子,用它的适应度值 F i t [ i ] Fit[i] Fit[i]和个体极值 p b e s t ( i ) p_{best}(i) pbest(i)比较,如果 F i t [ i ] > p b e s t ( i ) Fit[i]>p_{best}(i) Fit[i]>pbest(i),则用 F i t [ i ] Fit[i] Fit[i]替换掉 p b e s t ( i ) p_{best}(i) pbest(i)。
- 计算每个粒子,用它的适应度值 F i t [ i ] Fit[i] Fit[i]和全局极值 g b e s t ( i ) g_{best}(i) gbest(i)比较,如果 F i t [ i ] > g b e s t ( i ) Fit[i]>g_{best}(i) Fit[i]>gbest(i),则用 F i t [ i ] Fit[i] Fit[i]替换掉 g b e s t ( i ) g_{best}(i) gbest(i)。
- 根据式(4-1)和式(4-2)更新粒子的位置 x i x_i xi和速度 v i v_i vi。
- 如果满足结束条件(误差足够好或到达最大循环次数)退出,否则返回步骤2.
7. 手动实现PSO
function[xm,fv] = PSO(fitness,N,c1,c2,w,M,D)
% c1,c2:学习因子
% w:惯性权重
% M:最大迭代次数
% D:搜索空间维数
% N:初始化群体个体数目
% 初始化种群的个体(可以在这里限定位置和速度的范围)
format long;
for i = 1:N
for j=1:D
x(i,j) = randn; % 随机初始化位置
v(i,j) = randn; % 随即初始化速度
end
end
% 先计算各个粒子的适应度,并初始化pi和pg
for i=1:N
p(i) = fitness(x(i,:));
y(i,:) = x(i,:);
end
pg = x(N,:); % pg为全局最优
for i=1:(N-1)
if(fitness(x(i,:))<fitness(pg))
pg = x(i,:);
end
end
% 进入主要循环,按照公式依次迭代,直到满足精度要求
for t=1:M
for i=1:N % 更新速度、位移
v(i,:)=w*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(pg-x(i,:));
x(i,:)=x(i,:)+v(i,:);
if fitness(x(i,:)) < p(i)
p(i)=fitness(x(i,:));
y(i,:)=x(i,:);
end
if p(i) < fitness(pg)
pg=y(i,:);
end
end
Pbest(t)=fitness(pg);
end
% 输出结果
disp('目标函数取最小值时的自变量:')
xm=pg';
disp('目标函数的最小值为:')
fv=fitness(pg);
例1:求解下列函数的最小值:
f ( x ) = ∑ i = 1 30 x i 2 + x i − 6 f(x) = \sum^{30}_{i=1}x_i^2+x_i-6 f(x)=i=1∑30xi2+xi−6
function F=fitness(x)
F = 0;
for i = 1:30
F = F+x(i)^2+x(i)-6;
end
输入:
x = zeros(1,30);
[xm1,fv1] = PSO(@fitness,50,1.5,2.5,0.5,100,30)
后记:拜托 还有人问显示fitness未定义怎么办,找不到输出结果怎么办?? 软件入门都没搞定就不要急于求成好吗?
补入门知识:把手动实现PSO的代码保存为PSO.m,把function F=fitness(x)和后面4行代码保存为fitness.m。 然后再在命令行输入内容。
9. 自适应权重法
function[xm,fv] = PSO_adaptation(fitness,N,c1,c2,wmax,wmin,M,D)
% c1,c2:学习因子
% wmax:惯性权重最大值
% wmin:惯性权重最小值
% M:最大迭代次数
% D:搜索空间维数
% N:初始化群体个体数目
% 初始化种群的个体(可以在这里限定位置和速度的范围)
for i = 1:N
for j=1:D
x(i,j) = randn; % 随机初始化位置
v(i,j) = randn; % 随即初始化速度
end
end
%先计算各个粒子的适应度,并初始化个体最优解pi和整体最优解pg %
%初始化pi %
for i = 1:N
p(i) = fitness(x(i,:)) ;
y(i,:) = x(i,:) ;
end
%初始化pg %
pg = x(N,:) ;
%得到初始的全局最优pg %
for i = 1:(N-1)
if fitness(x(i,:)) < fitness(pg)
pg = x(i,:) ;
end
end
%主循环函数,进行迭代,直到达到精度的要求 %
for t = 1:M
for j = 1:N
fv(j) = fitness(x(j,:)) ;
end
fvag = sum(fv)/N ;
fmin = min(fv);
for i = 1:N %更新函数,其中v是速度向量,x为位置,i为迭代特征
if fv(i) <= fvag
w = wmin+(fv(i)-fmin)*(wmax-wmin)/(fvag-fmin) ; %依据早熟收敛程度和适应度值进行调整
else
w = wmax ;
end
v(i,:) = w*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(pg-x(i,:)) ;
x(i,:) = x(i,:)+v(i,:) ;
if fitness(x(i,:)) < p(i)
p(i) = fitness(x(i,:)) ;
y(i,:) = x(i,:) ;
end
if p(i) < fitness(pg)
pg = y(i,:) ;
end
end
Pbest(t) = fitness(pg) ;
end
%给出最后的计算结果 %
xm = pg' ;
fv = fitness(pg) ;
plot(Pbest)
xlabel('进化次数') ;
ylabel('适应度值') ;
例2:用自适应权重法求解函数
y = ( ( s i n ( x 1 2 + x 2 2 ) ) 2 − c o s ( x 1 2 + x 2 2 ) + 1 ) ( ( 1 + 0.1 × ( x 1 2 + x 2 2 ) ) 2 ) − 0.7 \large{y = \frac {((sin(x_1^2+x_2^2))^2-cos(x_1^2+x_2^2)+1)} {((1+0.1\times (x_1^2+x_2^2))^2)-0.7}} y=((1+0.1×(x12+x22))2)−0.7((sin(x12+x22))2−cos(x12+x22)+1)
其中,粒子数为50,学习因子均为2,惯性权重取值[0.6,0.8],迭代步数为100.
建立目标函数:
function y = AdaptFunc(x)
y = ((sin(x(1)^2+x(2)^2))^2-cos(x(1)^2+x(2)^2)+1)/((1+0.1*(x(1)^2+x(2)^2))^2)-0.7;
end
运行:
[xm,fv] = PSO_adaptation(@AdaptFunc,50,2,2,0.8,0.6,100,2)
10.线性递减权重法
function [ xm,fv ] = PSO_lin(fitness,N,c1,c2,wmax,wmin,M,D)
format long ;
%给定初始化条件
% fitness:适应度函数
% N: 初始化种群数目
% c1: 个体最优化学习因子
% c2: 整体最优化学习因子
% wmax: 惯性权重最大值
% wmin: 惯性权重最小值
% M: 最大迭代次数
% D: 搜索空间的维数
% xm: 最佳个体
% fv: 适应度值
%初始化种群个体%
for i = 1:N
for j = 1:D
x(i,j) = randn ; %随机初始化位置
v(i,j) = randn ; %随机初始化速度
end
end
%先计算各个粒子的适应度,并初始化个体最优解pi和整体最优解pg %
%初始化pi %
for i = 1:N
p(i) = fitness(x(i,:)) ;
y(i,:) = x(i,:) ;
end
%初始化pg %
pg = x(N,:) ;
%得到初始的全局最优pg %
for i = 1:(N-1)
if fitness(x(i,:)) < fitness(pg)
pg = x(i,:) ;
end
end
%主循环函数,进行迭代,直到达到精度的要求 %
for t = 1:M
for i = 1:N %更新函数,其中v是速度向量,x为位置,i为迭代特征
w = wmax-(t-1)*(wmax-wmin)/(M-1)
v(i,:) = w*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(pg-x(i,:)) ;
x(i,:) = x(i,:)+v(i,:) ;
if fitness(x(i,:)) < p(i)
p(i) = fitness(x(i,:)) ;
y(i,:) = x(i,:) ;
end
if p(i) < fitness(pg)
pg = y(i,:) ;
end
end
Pbest(t) = fitness(pg) ;
end
%给出最后的计算结果 %
xm = pg' ;
fv = fitness(pg) ;
11. 基于杂交(遗传算法)的算法
function [ xm,fv ] = PSO_breed(fitness,N,c1,c2,w,bc,bs,M,D)
format long ;
%给定初始化条件
% fitness:适应度函数
% N: 初始化种群数目
% c1: 个体最优化学习因子
% c2: 整体最优化学习因子
% w: 惯性权重
% bc: 杂交概率
% bs: 杂交池的大小比率
% M: 最大迭代次数
% D: 搜索空间的维数
% xm: 最佳个体
% fv: 适应度值
%初始化种群个体%
for i = 1:N
for j = 1:D
x(i,j) = randn ; %随机初始化位置
v(i,j) = randn ; %随机初始化速度
end
end
%先计算各个粒子的适应度,并初始化个体最优解pi和整体最优解pg %
%初始化pi %
for i = 1:N
p(i) = fitness(x(i,:)) ;
y(i,:) = x(i,:) ;
end
%初始化pg %
pg = x(N,:) ;
%得到初始的全局最优pg %
for i = 1:(N-1)
if fitness(x(i,:)) < fitness(pg)
pg = x(i,:) ;
end
end
%主循环函数,进行迭代,直到达到精度的要求 %
for t = 1:M
for i = 1:N %更新函数,其中v是速度向量,x为位置,i为迭代特征
v(i,:) = w*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(pg-x(i,:)) ;
x(i,:) = x(i,:)+v(i,:) ;
if fitness(x(i,:)) < p(i)
p(i) = fitness(x(i,:)) ;
y(i,:) = x(i,:) ;
end
if p(i) < fitness(pg)
pg = y(i,:) ;
end
r1 = rand() ;
if r1 < bc
numPool = round(bs*N) ; %杂交池中随机选取numPool个种群%
PoolX = x(1:numPool,:) ; %杂交池中的初始杂交父辈位置%
PoolVX = v(1:numPool,:) ; %杂交池中的初始杂交父辈速度%
for i = 1:numPool
seed1 = floor(rand()*(numPool-1))+1 ; %得到速度和位置的初始种子%
seed2 = floor(rand()*(numPool-1))+1 ;
pb = rand() ;
childxl(i,:) = pb*PoolX(seed1,:)+(1-pb)*PoolX(seed2,:) ; %子代的速度和位置计算
childvl(i,:) = (pb*PoolVX(seed1,:)+pb*PoolVX(seed2,:))*norm(pb*PoolVX(seed1,:))/norm(pb*PoolVX(seed1,:)+pb*PoolVX(seed2,:)) ;
end
x(1:numPool,:) = childxl ;
v(1:numPool,:) = childvl ;
end
end
end
%给出最后的计算结果 %
xm = pg' ;
fv = fitness(pg) ;
12. 基于自然选择
function [xm,fv]=PSO_nature(fitness,N,c1,c2,w,M,D)
% fitness:待优化的目标函数;
% N:粒子数目;
% c1:学习因子1;
% c2:学习因子2;
% w:惯性权重;
% M:最大迭代次数;
% D:自变量的个数;
% xm:目标函数取最小值时的自变量值;
% fv:目标函数的最小值。
format long;
for i=1:N
for j=1:D
x(i,j)=randn; %随机初始化位置
v(i,j)=randn; %随机初始化速度
end
end
for i=1:N
p(i)=fitness(x(i,:));
y(i,:)=x(i,:);
end
pg=x(N,:); %pg为全局最优
for i=1:(N-1)
if fitness(x(i,:))
pg=x(i,:);
end
end
for t=1:M
for i=1:N %速度、位移更新
v(i,:)=w*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(pg-x(i,:));
x(i,:)=x(i,:)+v(i,:);
fx(i)=fitness(x(i,:));
if fx(i)
p(i)=fx(i);
y(i,:)=x(i,:);
end
if p(i)
pg=y(i,:);
end
end
[sortf,sortx]=sort(fx); %将所有的粒子按适应值排序
exIndex=round((N-1)/2);
x(sortx((N-exIndex+1):N))=x(sortx(1:exIndex));%将最好的一半粒子的位置替换掉最差的一半
v(sortx((N-exIndex+1):N))=v(sortx(1:exIndex));%将最好的一半粒子的速度替换掉最差的一半
end
xm=pg';
fv=fitness(pg);
13.基于模拟退火
function [xm,fv]=PSO_lamda(fitness,N,c1,c2,lamda,M,D)
% fitness:待优化的目标函数;
% N:粒子数目;
% c1:学习因子1;
% c2:学习因子2;
% lamda:退火常数;
% M:最大迭代次数;
% D:自变量的个数;
% xm:目标函数取最小值时的自变量值;
% fv:目标函数的最小值。
format long;
for i=1:N
for j=1:D
x(i,j)=randn; %随机初始化位置
v(i,j)=randn; %随机初始化速度
end
end
for i=1:N
p(i)=fitness(x(i,:));
y(i,:)=x(i,:);
end
pg=x(N,:); %pg为全局最优
for i=1:(N-1)
if fitness(x(i,:))
pg=x(i,:);
end
end
T=-fitness(pg)/log(0.2); %初始温度
for t=1:M
groupFit=fitness(pg);
for i=1:N %当前温度下各个pi的适应值
Tfit(i)=exp(-(p(i)-groupFit)/T);
end
SumTfit=sum(Tfit);
Tfit=Tfit/SumTfit;
pBet=rand();
for i=1:N %用轮盘赌策略确定全局最优的某个替代值
ComFit(i)=sum(Tfit(1:i));
if pBet<=ComFit(i)
pg_plus=x(i,:);
break;
end
end
C=c1+c2;
ksi=2/abs(2-C-sqrt(C^2-4*C)); %速度压缩因子
for i=1:N
v(i,:)=ksi*(v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(pg_plus-x(i,:)));
x(i,:)=x(i,:)+v(i,:);
if fitness(x(i,:))
p(i)=fitness(x(i,:));
y(i,:)=x(i,:);
end
if p(i)
pg=y(i,:);
end
end
T=T*lamda;
Pbest(t) = fitness(pg) ;
end
xm=pg';
fv=fitness(pg);
14. MATLAB粒子群工具箱
添加工具箱的具体步骤就不在这里说了,网上有很多。
例3:计算如下函数的最小值:
z = 0.4 ∗ ( x − 2 ) 2 + 0.3 ∗ ( y − 4 ) 2 − 0.7 , x ∈ [ − 40 , 40 ] , y ∈ [ − 40 , 40 ] z = 0.4*(x-2)^2 + 0.3 * (y-4)^2 -0.7, x\in[-40,40] , y\in[-40,40] z=0.4∗(x−2)2+0.3∗(y−4)2−0.7,x∈[−40,40],y∈[−40,40]
-
定义待优化的MATLAB代码:
function z = pso_func(in) n = size(in); x = in(:,1); y = in(:,2); nx = n(1); for i=1:nx temp = 0.4*(x(i)-2)^2+0.3*(y(i)-4)^2-0.7; z(i,:) = temp; end -
调用PSO算法的核心函数:
pso_Trelea_vectorizedclear clc x_range = [-40,40]; y_range = [-40,40]; range = [x_range;y_range]; Max_V = 0.2*(range(:,2)-range(:,1)); n = 2; pso_Trelea_vectorized('pso_func',n,Max_V,range)
执行即可得到答案。
在PSO算法函数pso_Trelea_vectorized173行中,PSO参数设置如下:
Pdef = [100 2000 24 2 2 0.9 0.4 1500 1e-25 250 NaN 0 1];
- 100:MATLAB命令窗口进行显示的间隔数
- 2000:最大迭代次数
- 24:初始化种子数,种子数越多,越有可能收敛到全局最优值,但算法收敛速度慢
- 2:算法的加速度参数,分别影响局部最优值和全局最优值,一般不需要修改
- 0.9和0.4为初始时刻和收敛时刻的加权值,一般不需要修改
- 1500:迭代次数超过此值时,加权值取其最小
- 1e-25:算法终止条件之一,当两次迭代中对应的种群最优值小于此阈值时,算法停止
- 250:算法终止条件之一,取NaN时表示为非约束下的优化问题(即没有附加约束方程)
- 0:制定采用何种PSO类型,0表示通常的PSO算法
- 1:说明是否指定种子,0表示随机产生种子,1表示用户自行产生种子